Как вычисляются наибольшие нормальные напряжения при косом изгибе?
Покажем это на конкретном примере. Рассмотрим консольную балку прямоугольного поперечного сечения длиной l, нагруженную вертикальной силой P (рис. 9.1). Пусть балка расположена по отношению к нагрузке таким образом, что ее главная центральная ось y (ось симметрии) составляет некоторый малый угол 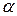 с направлением действия нагрузки. Пусть такой перекос обусловлен,например, технологическим браком при сборке конструкции.
с направлением действия нагрузки. Пусть такой перекос обусловлен,например, технологическим браком при сборке конструкции.
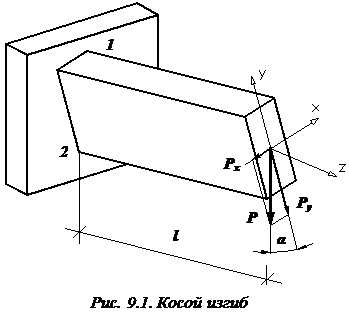
Разложим силу P на две составляющие:
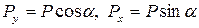 .
.
Воспользуемся принципом независимости действия сил и рассмотрим действие каждой из этих составляющих в отдельности.
Нагрузки 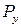 и
и 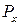 вызывают в поперечном сечении, расположенном на некотором расстоянии z от правого конца балки, изгибающие моменты, абсолютные значения которых определяются по формулам:
вызывают в поперечном сечении, расположенном на некотором расстоянии z от правого конца балки, изгибающие моменты, абсолютные значения которых определяются по формулам:
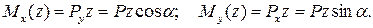
Оба изгибающих момента будут наибольшими в заделке:
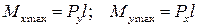 .
.
Суммарные нормальные напряжения при косом изгибе в произвольном поперечном сечении балки для некоторой точки с координатами x и y вычисляются по следующей формуле
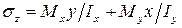 , (9.1)
, (9.1)
где 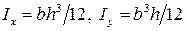 – главные моменты инерции; h – высота, а b – ширина поперечного сечения балки.
– главные моменты инерции; h – высота, а b – ширина поперечного сечения балки.
Значения изгибающих моментов и координат исследуемой точки подставляются в формулу (9.1) по их абсолютному значению, а знак каждого из слагаемых определяется в целом, согласно физическому смыслу.
Наибольшие нормальные напряжения возникнут в поперечном сечении, расположенном в заделке, в точках 1 и 2, которые наиболее удалены от соответствующих нейтральных осей и имеют следующие абсолютные значения координат: 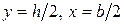 .
.
При этом, очевидно, что в точке 1 напряжения будут растягивающими:
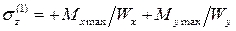 , (9.2)
, (9.2)
а в точке 2 – точно такими же по величине, но сжимающими:
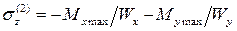 . (9.3)
. (9.3)
В формулах (9.2) и (9.3) 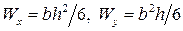 – моменты сопротивления балки при изгибе относительно главных центральных осей инерции.
– моменты сопротивления балки при изгибе относительно главных центральных осей инерции.
9.4. Как определяется положение нулевой (или нейтральной) линии при косом изгибе?
Напомним, что нулевой линией (НЛ) называется геометрическое место точек поперечного сечения стержня, в которых нормальные напряжения равны нулю. Из этого определения легко и определяется положение НЛ. Приравнивая правую часть выражения (9.1) к нулю, получим:
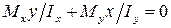 ,
,
отсюда
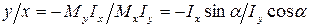 . (9.4)
. (9.4)
Обозначим через 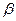 угол наклона НЛ к оси x. Тогда
угол наклона НЛ к оси x. Тогда 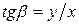 , и уравнение НЛ (9.4) принимает следующий вид:
, и уравнение НЛ (9.4) принимает следующий вид:
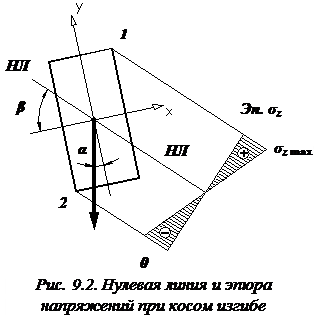
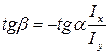 . (9.5)
. (9.5)
Из уравнения (9.5) видно, что в общем случае (когда 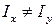 ) НЛ при косом изгибе не проходит перпендикулярно к силовой линии (рис. 9.2), поскольку
) НЛ при косом изгибе не проходит перпендикулярно к силовой линии (рис. 9.2), поскольку 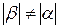 . Лишь в частном случае, когда значения главных центральных моментов инерции равны между собой (
. Лишь в частном случае, когда значения главных центральных моментов инерции равны между собой ( 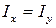 ), угол между НЛ и силовой линией будет прямым (
), угол между НЛ и силовой линией будет прямым ( 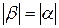 ), и это означает, что изгиб будет прямым.
), и это означает, что изгиб будет прямым.
Заметим, что для балок с поперечным сечением типа квадрат, круг и т. п., у которых все центральные оси являются главными, косой изгиб невозможен.
