Симплексный метод и двойственные задачи

1-30. Решить задачи симплекс-методом, дать решению геометрическую интерпретацию, записать двойственную задачу и ее решение. Во всех заданиях иметь в виду, что переменные неотрицательны.

1.	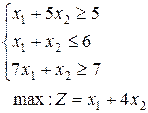2.	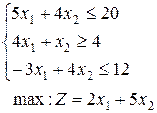3.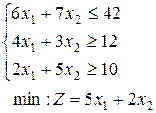
4.	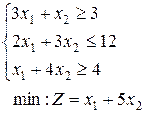5.	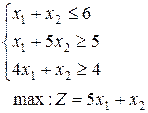6.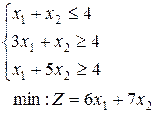
7.	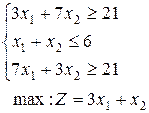8.	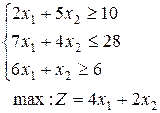9.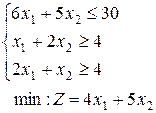
10.	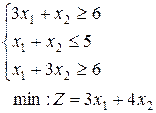11.	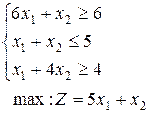12.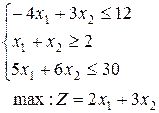
13.	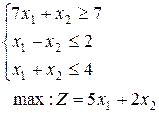14.	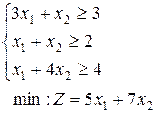15.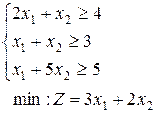
16.	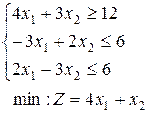17.	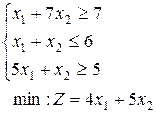18.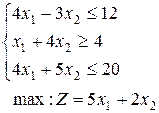
19.	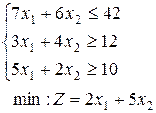20.	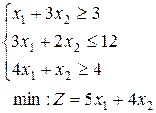21.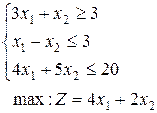
22.	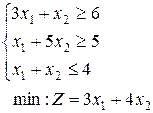23.	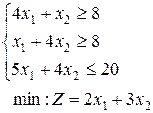24.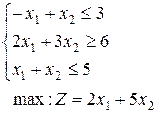
25.	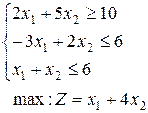26.	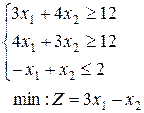27.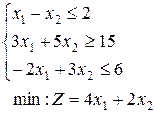
28.	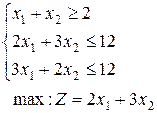29.	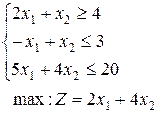30.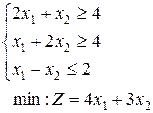

Матричные игры

1-30. Проанализировать игру, используя принцип минимакса. Найти решение в смешанных стратегиях методами линейного программирования.

1.						2.
3.						4.
5.						6.
7.						8.
9.						10.
11.						12.
13.						14.
15.						16.
17.						18.
19.						20.
21.						22.
23.						24.
25.						26.
27.						28.
29.						30.

Транспортные задачи

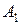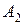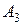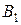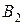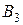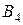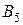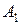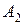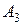1-30. Имеются три пункта поставки , , однородного груза и пять пунктов , , , , потребления этого груза. В пунктах , и находится груз соответственно в количестве , и 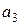т. В пункты 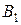, , 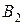, 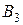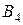и 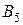требуется доставить соответственно 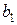, , , 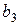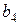и 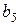т. Транспортные тарифы 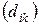приведены в следующей матрице-таблице:

Пункты поставки	Пункты потребления

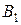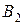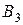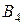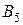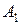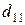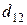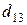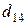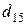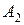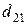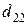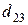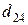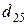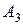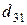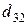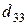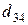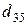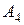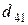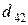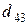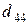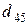Найти такой план закрепления поставщиков однородного груза за потребителями, чтобы общие затраты по перевозкам были минимальными.

1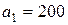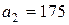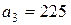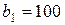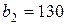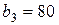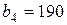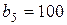.	, , ,	, , ,	, ;	2.	, , ,	, , ,	, ;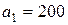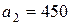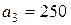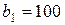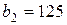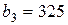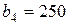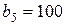
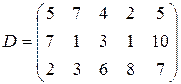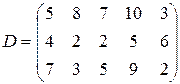3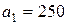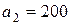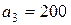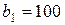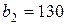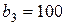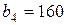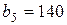.	, , ,	, , ,	,	4.	, , ,	, , ,	,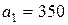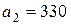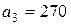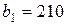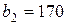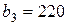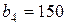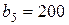
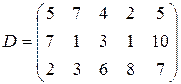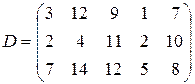5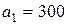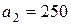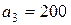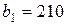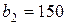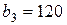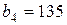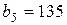.	, , ,	, , ,	,	6.	, , ,	, , ,	,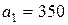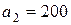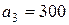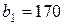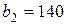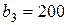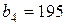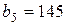

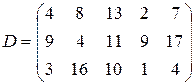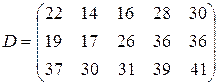7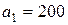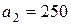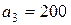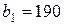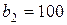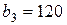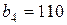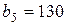.	, , ,	, , ,	,	8.	, , ,	, , ,	,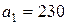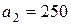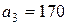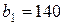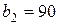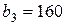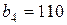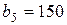
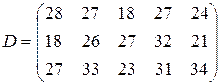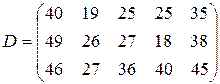9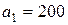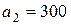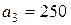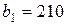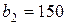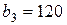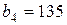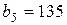.	, , ,	, , ,	,	10.	, , ,	, , ,	,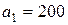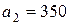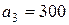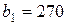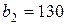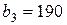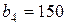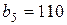
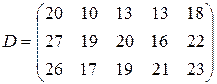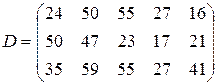11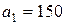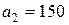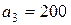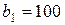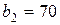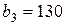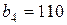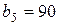.	, , ,	, , ,	,	12.	, , ,	, , ,	,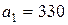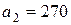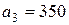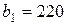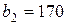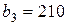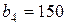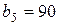
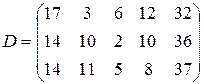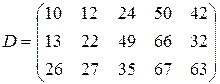13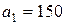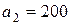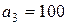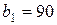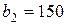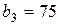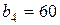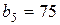.	, , ,	, , ,	,	14.	, , ,	, , ,	,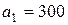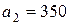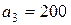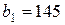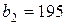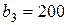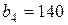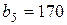
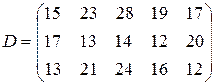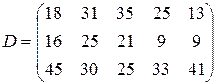15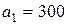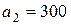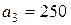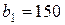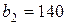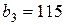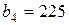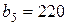.	, , ,	, , ,	,	16.	, , ,	, , ,	,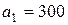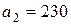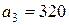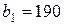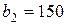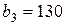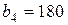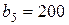

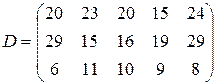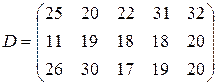17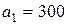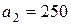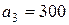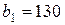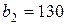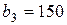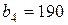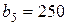.	, , ,	, , ,	,	18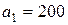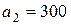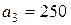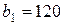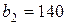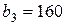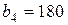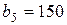.	, , ,	, , ,	,
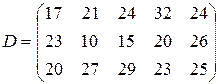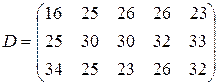