Порядок выполнения работы. Ввод текста на всех этапах решения задачи будем осуществлять с помощью ком­бинации

Ввод текста на всех этапах решения задачи будем осуществлять с помощью ком­бинации клавиш Shift+" (двойная кавычка), что позволит создать текстовую об­ласть. Введем на рабочем листе первый пункт расчета (рис. 1.2). Он будет выгля­деть так:

1. Задание исходных данных одноканалъной замкнутой CMО.
Последовательно введем исходные данные:

- интенсивность обслуживания требований 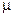:=29;

- интенсивность поступления одного требования на обслуживание 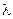:=6;

- число требований, функционирующих в системе, m:= 5.

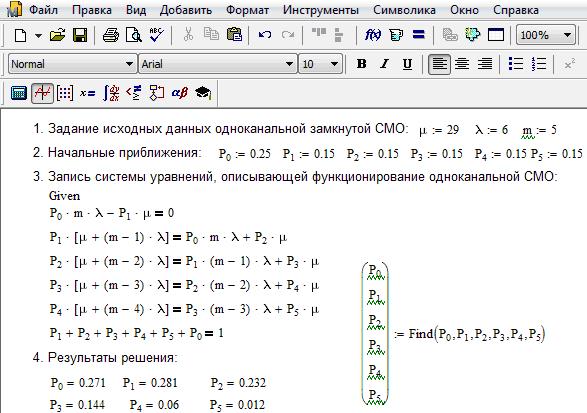
Рис. 1.2 - Определение параметров функционирования
одноканальной замкнутой СМО в системе Mathcad

Для решения задачи воспользуемся блоком функций Given ... Find. Его при­менение требует предварительного задания начальных приближений. Введем на рабочем листе второй пункт расчета (рис. 1.2). Он будет выгля­деть так:

2. Начальные приближения.

Последовательно наберем начальные приближенные значения искомых пара­метров:

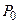:= 0,25 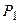:= 0,15 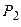:= 0,15 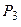:= 0,15 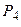:= 0,15 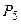:= 0,15

Сумма вероятностей всех состояний должна быть равна 1.

Введем на рабочем листе третий пункт расчета (рис. 1.1). Он будет выгля­деть так:

3. Запись системы уравнений, описывающей функционирование одноканалъной СМО.

Вначале записывается ключевое слово Given (Дано), которое может быть на­печатано прописными, строчными буквами или начинаться с прописной.

Ниже вводится исходная система уравнений.

Для примера ограничимся рассмотрением одноканальной замкнутой систе­мы, в которой обслуживаются пять требований. Интенсивность поступления одного требования на обслуживание 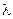равна трем поступлениям в час. Ин­тенсивность обслуживания в канале 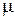составляет 29 обслуживании в час. Эта система алгебраических уравнений будет выглядеть так:

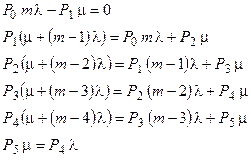
Однако в представленном виде определитель системы будет равен нулю – сис­тема вырождена. Во избежание этой ситуации заменим последнее выражение следующим равенством:

.

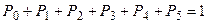В заключение вводится вектор искомых величин. Для этого в поле рабочего листа (рис. 1.2) определим местоположение вектора, который должен на­ходиться несколько ниже системы равенств. Если в окне имеется панель инструментов Math (Математика), щелкнем по кнопке с изображением матрицы. Появится окно Matrix(Матрица), далее – по кнопке с аналогич­ным изображением или воспользуемся комбинацией клавиш Ctrl+M. В обо­их случаях появится диалоговое окно Insert Matrix(Вставить матрицу). В тек­стовых полях Rows(Строки) и Columns(Столбцы) этого диалогового окна вставляем нужное число строк и столбцов, в нашей задаче – 6 и 1 соответ­ственно.

После щелчка по клавише ОК появится шаблон с метками для ввода иско­мых параметров ( 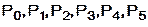). Осуществим эту операцию, подведя кур­сор или указатель мыши к каждой метке. Затем произведем ввод знака при­сваивания и имени встроенной функции Find( 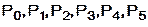). Введем на рабочем листе четвертый пункт расчета (рис. 1.2). Он будет вы­глядеть так:

4. Результаты решения.

Для получения результатов расчета искомых величин достаточно набрать имя нужного параметра и знак равенства, нажав соответствующую клавишу или щелкнув по кнопке со знаком равенства, расположенной в верхнем левом углу панели инструментов Evalu...(Вычисления).

Анализируя полученные результаты решения в системе Mathcad, можно за­метить, что значения для параметров 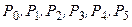совпадают с соответ­ствующими значениями, полученными вручную.

Рассмотрим неустановившийся режим работы системы массового обслужи­вания, когда ее основные вероятностные характеристики зависят от времени, например в течение 0,3 часа. В этом случае интенсивности входных и выход­ных потоков для каждого состояния будут сбалансированы, но уже с учетом производных вероятностей. Таким образом, мы будем иметь систему обыкно­венных дифференциальных уравнений, описывающих функционирование одноканальной замкнутой системы при неустановившемся режиме. Для примера ограничимся рассмотрением той же самой системы, в которой обслу­живаются пять требований. Интенсивность поступления одного требования на обслуживание 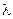равна трем поступлениям в час. Интенсивность обслуживания в канале 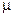составляет 29 требований в час. Эта система обыкновенных дифференциальных уравнений будет выглядеть так:

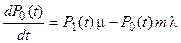
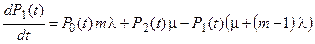
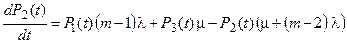
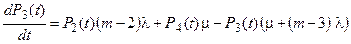
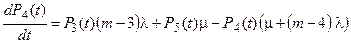
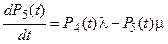
На рис. 1.3 представлены начальные исходные данные и система дифферен­циальных уравнений, описывающая функционирование одноканальной замк­нутой СМО при неустановившемся режиме работы.

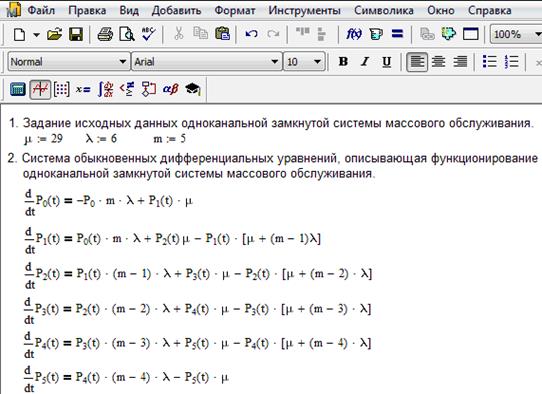
Рис. 1.3. Описание функционирования одноканальной замкнутой системы
массового обслуживания при неустановившемся режиме

На рис. 1.4 система дифференциальных уравнений представлена в доступном для решения виде в системе Mathcad. Здесь изображены правые части системы дифференциальных уравнений в форме вектора-столбца, каждый элемент которого определяет значение правой части соответствующего уравнения на каждом шаге ин­тегрирования (решения), и даны начальные значения искомых параметров тоже в ви­де вектора-столбца. В нижней части рисунка определены начальное и конечное вре­мя интегрирования и число шагов решения системы дифференциальных уравнений.

На рис. 1.5 приведено решение системы дифференциальных уравнений одноканальной замкнутой СМО с использованием встроенной функции rkfixed(P, t0, t1, N, D), реализующей метод Рунге-Кутта с фиксированным шагом. Для вызова этой функции щелкните по пункту Function (Функция) падающего меню пункта Insert (Вставка) главного меню или нажмите комбинацию клавиш Ctrl+ E. Появится диалоговое окно Insert Function (Вставить функцию). В списке Function Category (Категория функции) найдите строку Differential Equation Solving (Решение дифференциального уравнения) и щелкните по ней левой кноп­кой мыши. В правом поле Function Name (Имя функции) появится имя функции rkfixed. После этого щелкните по кнопке ОК.

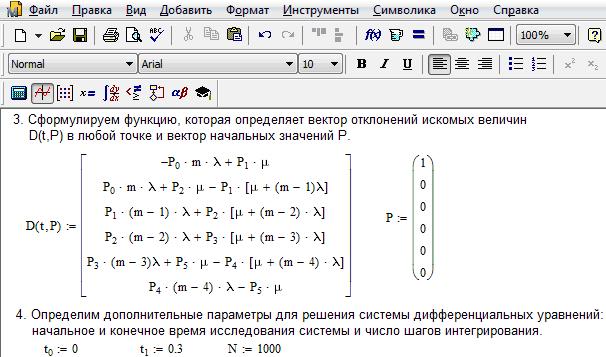
Рис. 1.4. Описание функционирования одноканальной замкнутой системы
массового обслуживания при неустановившемся режиме

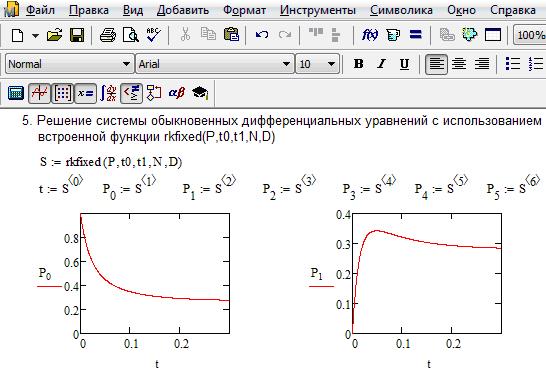
Рис. 1.5. Результаты функционирования одноканальной замкнутой СМО
при неустановившемся режиме (начало)

Можно сразу найти функцию rkfixed в правом поле Function Name диало­гового окна, после чего щелкнуть по ней мышью, а затем по кнопке ОК, но это займет больше времени. В обоих случаях в нижних полях диалогового окна бу­дет дано правильное написание выбранной функции со всеми аргументами, а также краткое описание ее действий. На рис. 1.5 приведено графическое ре­шение системы дифференциальных уравнений для первых двух искомых па­раметров. Иными словами, графически представлено поведение первых двух параметров 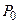и 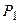– вероятности отсутствия требований и возможности наличия в системе одного требования соответственно в зависимости от времени протекания процесса.

На рис. 1.6 представлено графическое решение системы дифференциальных уравнений для остальных четырех искомых параметров. Другими словами – поведение искомых параметров 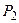, , 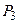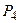и 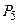– вероятности наличия в системе двух, трех, четырех и пяти требований соответственно в зависимости от времени протекания процесса.

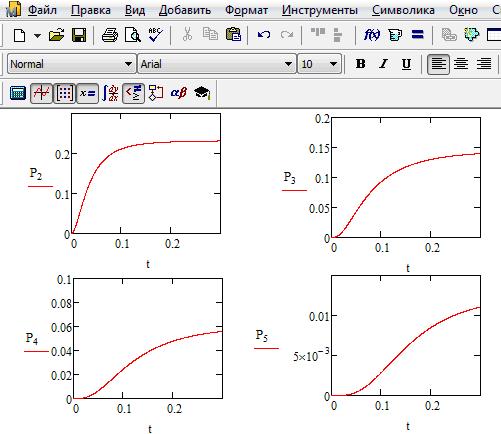
Рис. 1.6. Результаты функционирования одноканальной замкнутой СМО при
неустановившемся режиме, представленные в графическом виде (окончание)

Анализируя графическое решение системы обыкновенных дифференциальных уравнений, описывающей функционирование заданной одноканальной замкнутой СМО, можно заметить, что примерно через 0,3 часа система переходит в установившийся режим работы. При этом значения вероятностей состояний установившегося режима работы системы при решении совокупности обыкновенных дифференциальных уравнений практически полностью соответствуют решению системы алгебраических уравнений для установившегося режима работы:

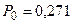
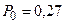
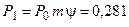
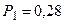
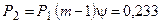
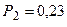
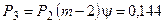
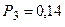
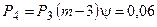
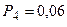
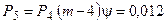
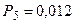
На рис. 1.7 представлен фрагмент результатов решения системы обыкновен­ных дифференциальных уравнений в численном виде.

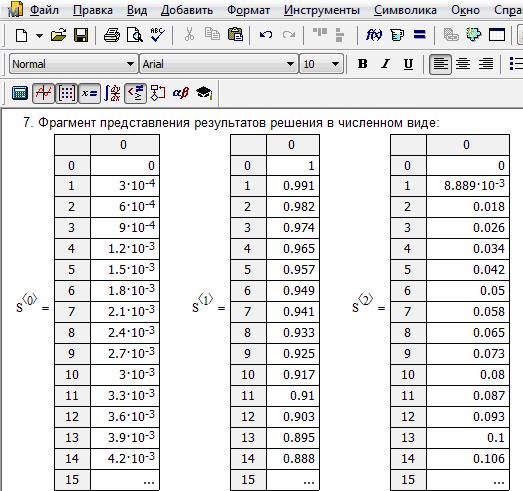
Рис. 1.7. Фрагмент результатов решения системы обыкновенных
дифференциальных уравнений в численном виде для одноканальной замкнутой СМО