Расчет цепи постоянного тока методом контурных токов

Электрическая цепь постоянного тока остается неизменной для данного метода.

Ме́тод ко́нтурных то́ков — метод сокращения размерности системы уравнений, описывающей электрическую цепь.

Метод контурных токов — метод расчёта электрических цепей, при котором за неизвестные принимаются токи в контурах, образованных некоторым условным делением электрической цепи.

Основные принципы

Любая электрическая цепь, состоящая из Р рёбер (ветвей, участков, звеньев) и У узлов, может быть описана системой уравнений в соответствии с 1-м и 2-м правилами Кирхгофа. Число уравнений в такой системе равно Р, из них У–1 уравнений составляется по 1-му закону Кирхгофа для всех узлов, кроме одного; а остальные Р–У+1 уравнений – по 2-му закону Кирхгофа для всех независимых контуров. Поскольку независимыми переменными в цепи считаются токи рёбер, число независимых переменных равно числу уравнений, и система разрешима.

Существует несколько методов сократить число уравнений в системе. Одним из таких методов является метод контурных токов.

Метод использует тот факт, что не все токи в рёбрах цепи являются независимыми. Наличие в системе У–1 уравнений для узлов означает, что зависимы У–1 токов. Если выделить в цепи Р–У+1 независимых токов, то систему можно сократить до Р–У+1 уравнений. Метод контурных токов основан на очень простом и удобном способе выделения в цепи Р–У+1 независимых токов.

Метод контурных токов основан на допущении, что в каждом из Р–У+1 независимых контуров схемы циркулирует некоторый виртуальный контурный ток. Если некоторое ребро принадлежит только одному контуру, реальный ток в нём равен контурному. Если же ребро принадлежит нескольким контурам, ток в нём равен сумме соответствующих контурных токов (с учётом направления обхода контуров). Поскольку независимые контура покрывают собой всю схему (т.е. любое ребро принадлежит хотя бы одному контуру), то ток в любом ребре можно выразить через контурные токи, и контурные токи составляют полную систему токов.

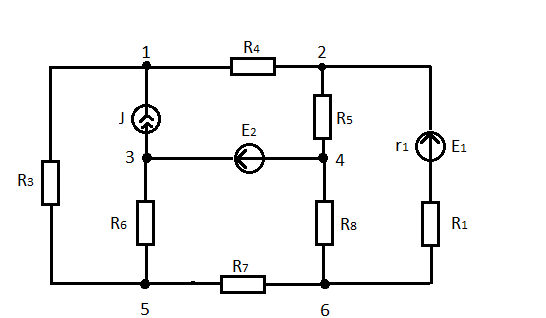Расчет электрической цепи постоянного тока методом контурных токов:

В каждом контуре выбираем контурный ток, например I11 для первого контура, и записываем уравнения:

Далее находим токи на контурах, расписываем токи через контуры:

Получаем конечный результат:

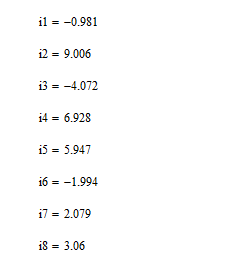
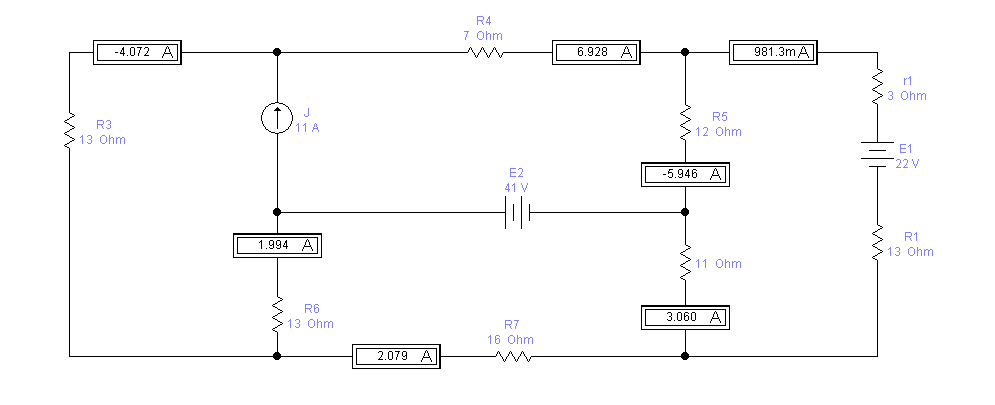
Выполним моделирование, используя Electronics Workbench:

Сводная таблица результатов по трем методам:

	По законам Кирхгофа	Метод узловых потенциалов	Метод контурных токов
I1	0,981	0,981	0,981
I2	9,006	9,006	9,006
I3	4,072	4,072	4,072
I4	6,928	6,928	6,928
I5	5,947	5,947	5,947
I6	1,994	1,994	1,994
I7	2,079	2,079	2,079
I8	3,06	3,06	3,06

Составим баланс мощностей:

P_R=I^2*R P_E=E*I P_J=(Ф_А-Ф_В)*J

P_{потребителей}=P_R1+r1+P_R3+P_R4+P_R5+P_R6+P_R7+P_R8

P_{источников}=(Ф₁-Ф₃)*J+P_E1+P_E2

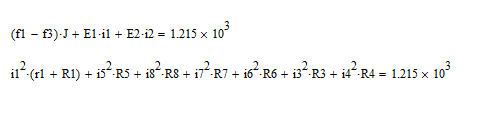
P_{источников}=

P_{потребителей}=

P_{потребителей}= P_{источников}

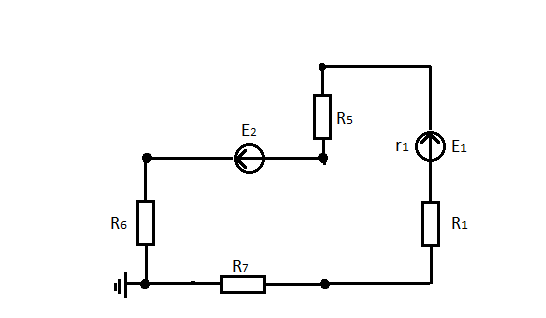
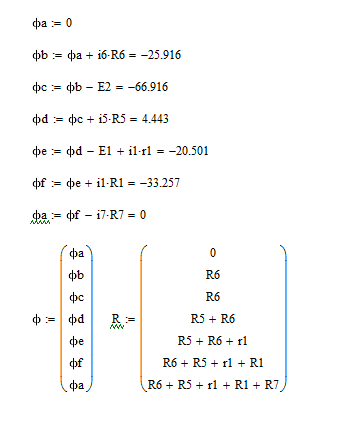
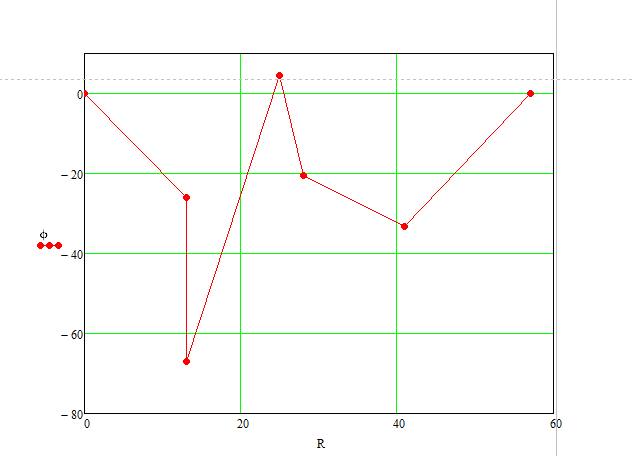
Составим потенциальную диаграмму для контура, который включает оба источника ЭДС: