Системные переменные и константы
Системные переменные и константы устанавливаются системой при ее загрузке или автоматически формируются в процессе вычислений. Некоторые
из них приведены в табл. 3.8.
Таблица 3.8
| Имя | Функция |
| ans | Результат выполнения последней операции |
| computer | Возвращает строку с информацией о типе компьютера, на котором установлена система Matlab |
| i или j | Мнимая единица (равная sqrt(–1)), которая используется для задания мнимой части комплексных чисел |
| Inf | Возвращает представление положительной бесконечности для машинной арифметики |
| pi | Число p (отношение длины окружности к ее диаметру), pi возвращает число с плавающей запятой, ближайшее к значению p |
Существуют также функции для обработки множеств, побитовой логической обработки, даты и времени и т. д.
Специальные символы
Специальные символы предназначены для создания самых разнообразных объектов входного языка и языка программирования системы и придания им различных форм.
Таблица 3.9
| Обозначение | Функция |
| : | Двоеточие: формирование подвекторов и подматриц из векторов и матриц. Оператор – один из наиболее часто используемых в системе Matlab |
| ( ) | Круглые скобки: а) задание порядка выполнения операций в арифметических выражениях, б) указание последовательности аргументов функции, в) указание индексов элемента вектора или матрицы |
| [ ] | Квадратные скобки: формирование векторов и матриц |
| { } | Фигурные скобки: формирование массивов ячеек |
| . | Десятичная точка: отделение дробной части чисел от целой |
| . | Точка: выделение поля структуры |
| ... | Продолжение строки |
| , | Запятая: а) разделение индексов элементов матрицы, б) разделение аргументов функции, в) разделение операторов языка Matlab |
| ; | Точка с запятой: а) внутри круглых скобок – разделение строк матриц, б) в конце операторов – запрет вывода на экран результата вычислений |
| % | Комментарий |
| = | Присваивание |
| ' | Транспонирование |
| [,] и [;] | Горизонтальная и вертикальная конкатенации соответственно |
Некоторые специальные символы приведены в табл. 3.9.
Элементарные функции
1. Алгебраические и арифметические функции. В системе Matlab определены представленные в табл. 3.10 алгебраические и арифметические функции.
Таблица 3.10
| Наименование | Назначение и возвращаемые значения |
| abs(X) | Абсолютная величина для каждого элемента вектора X |
| ехр(Х) | Экспонента для каждого элемента X |
| log(X), log2(X), log10(X) | Логарифмы элементов массива X: натуральный, по основаниям 2 и 10 соответственно |
| sqrt(X) | Квадратный корень каждого элемента массива X |
| G=gcd(A, В) | Массив, содержащий наибольшие общие делители соответствующих эле-ментов массивов целых чисел А и В |
| lcm(A, B) | Наименьшие общие кратные для соответствующих парных элементов массивов А и В. Массивы А и В должны содержать положительные целые числа и иметь одинаковую размерность (любой из них может быть скаляром) |
| mod(A, B) | Остаток от деления A на B |
Таблица 3.11
| Матрица X | Операции с X | Результат выполнения | ||
| »X = [1 –2 4.3 –5 7] X = 1.00 –2.00 4.30 –5.00 7.00 | »abs(X) | ans = 1.0000 2.0000 4.3000 5.0000 7.0000 | ||
| »exp(X) | ans = 1.0e+003 * 0.0027 0.0001 0.0737 0.0000 1.0966 | |||
| »log(X) | ans = 0 0.6931+3.1416i 1.4586 1.6094+3.1416i 1.9459 | |||
| »log2(X) | ans = 0 1.0000+4.5324i 2.1043 2.3219+4.5324i 2.8074 | |||
| »log10(X) | ans = 0 0.3010+1.3644i 0.6335 0.6990+1.3644i 0.8451 | |||
| »sqrt(X) | ans = 1.0000 0+1.4142i 2.0736 0+2.2361i 2.6458 | |||
| Матрица A | Матрица B | Операция 1 | Операция 2 | Операция 3 |
| »A = [1 23 1 34] A = 1 23 1 34 | »B =[5 12 1 1] B = 5 12 1 1 | »G = gcd(A, B) G = 1 1 1 1 | »lcm(A, B) ans = 5 276 1 34 | »mod(A, B) ans = 1 11 0 0 |
Пример 3.1. Использование функций иллюстрирует табл. 3.11.
2. Функции комплексного аргумента. Для работы с комплексными числами и данными в Matlab используются функции комплексного аргумента (табл. 3.12).
Таблица 3.12
| Наименование | Назначение |
| angle(Z) | Возвращает аргумент комплексного числа в радианах для каждого элемента массива комплексных чисел Z. Углы находятся в диапазоне [–p; +p]. Для комплексного Z модуль и аргумент вычисляются следующим образом: R=abs(Z) – модуль, theta = angle(Z) – аргумент. При этом формула Z=R.*exp(i*theta) дает переход от показательной формы представления комплексного числа к алгебраической |
| imag(Z) | Возвращает мнимые части всех элементов массива Z |
| real(Z) | Возвращает вещественные части всех элементов комплексного массива Z |
| conj(Z) | Возвращает число, комплексно-сопряженное аргументу Z. Если Z комплексное, то conj(Z) = real(Z) – i*imag(Z) |
Таблица 3.13
| Матрица | Операция 1 | Операция 2 | Операция 3 |
| »Z = 5–i*3 Z = 5.0000 – 3.0000i | »theta = angle(Z) theta = –0.5404 | »R = abs(Z) R = 5.8310 | »Z = R .* exp(i*theta) Z = 5.0000 – 3.0000i |
| »Z = [2+i, 1+2i, 2+3i]; | »imag(Z) ans = 1 2 3 | »real(Z) ans = 2 1 2 | »conj(2+i) ans = 2.0000 – 1.0000i |
Пример 3.2. Работу с комплексными аргументами иллюстрирует табл. 3.13.
3. Тригонометрические и обратные им функции. Тригонометрические и обратные тригонометрические функции (табл. 3.14) вычисляются для каждого элемента массива. Входной массив допускает комплексные значения (все
углы в функциях задаются в радианах).
Таблица 3.14
| Наименование | Назначение и возвращаемые значения |
| acos(X) | Арккосинус для каждого элемента X. Для действительных значений X из области [–1, 1] возвращает действительное значение из диапазона [0, p]; для действительных значений X вне области [–1, 1] – комплексное число |
| acot(X) | Арккотангенс для каждого элемента X |
| acsc(X) | Арккосеканс для каждого элемента X |
| asec(X) | Арксеканс для каждого элемента X |
| asin(X) | Арксинус для каждого элемента X |
| atan(X) | Арктангенс для каждого элемента X |
| atan2(Y, X) | Массив Р той же размерности, что X и Y, содержащий поэлементно арктангенсы отношения вещественных частей Y и X |
| cos(X) | Косинус для каждого элемента X |
| cot(X) | Котангенс для каждого элемента X |
| csc(X) | Косеканс для каждого элемента X |
| sec(X) | Массив той же размерности что и X, состоящий из секансов элементов X |
| tan(X) | Тангенс для каждого элемента X |
Таблица 3.15
| Матрица | Операция 1 | Операция 2 |
| »X = [–0.5 0 0.5] X = –0.5000 0 0.5000 | »Y = cos(X) Y = 0.8776 1.0000 0.8776 | »Y = sin(X) Y = –0.4794 0 0.4794 |
Пример 3.3. Результаты применения тригонометрических функций представлены в табл. 3.15.
4. Гиперболические и обратные им функции. Гиперболические функции (табл. 3.16) вычисляются для каждого элемента массива. Входной массив до-
пускает комплексные значения.
Таблица 3.16
| Наимено-вание | Назначение функции, выполняемой для каждого элемента X | Наимено-вание | Назначение функции, выполняемой для каждого элемента X |
| acosh(X) | Гиперболический арккосинус | cosh(X) | Гиперболический косинус |
| acoth(X) | Гиперболический арккотангенс | coth(X) | Гиперболический котангенс |
| acsch(X) | Гиперболический арккосеканс | csch(X) | Гиперболический косеканс |
| asech(X) | Гиперболический арксеканс | sech(X) | Гиперболический секанс |
| asinh(X) | Гиперболический арксинус | sinh(X) | Гиперболический синус |
| atanh(X) | Гиперболический арктангенс | tanh(X) | Гиперболический тангенс |
Таблица 3.17
| Применение функций для скалярного значения | |||||
| »Y = acosh(0.7) Y = 0 + 0.7954i | »Y = acoth(0.1) Y = 0.1003 + 1.5708i | »Y = acsch(1) Y = 0.8814 | »Y = asech(4) Y = 0 + 1.3181i | »Y = asinh(2.456) Y = 1.6308 | |
| Применение функций для вектора | |||||
| »Х = [0.84 0.16 1.39]; | »Х = [1 23]; | ||||
| »atanh(X) | ans = 1.2212 0.1614 0.9065 + 1.5708i | »cosh(X) | ans = 1.0e+009 * 0.0000 4.8724 | ||
Пример 3.4. Варианты задания аргументов для гиперболических функций и результаты их выполнения приведены в табл. 3.17.
5. Функции округления и знака. Ряд особых функций (табл. 3.18) служат для выполнения операций округления числовых данных и анализа их знака.
Таблица 3.18
| Наимено-вание | Назначение |
| fix(A) | Массив А с элементами, округленными до ближайшего к нулю целого числа. Для комплексного А действительные и мнимые части округляются отдельно |
| floor(A) | Массив А с элементами, представляющими ближайшее меньшее или равное соответствующему элементу А целое число. Для комплексного А действительные и мнимые части преобразуются отдельно |
| rem(X, Y) | X – fix(X./Y).*Y, где fix(X./Y) – целая часть от частного X./Y |
| ceil(A) | Ближайшее большее или равное А целое число. Для комплексного А действительные и мнимые части округляются отдельно |
| round(X) | Округленные до ближайшего целого элементы массива X. Для комплексного X действительные и мнимые части округляются отдельно |
| sign(X) | Массив Y той же размерности, что и X, где каждый из элементов Y равен: 1, если соответствующий элемент X больше 0; 0, если соответствующий элемент X равен 0; –1, если соответствующий элемент X меньше 0. Для ненулевых действительных и комплексных X – sign(X)=X./abs(X) |
Таблица 3.19
| Варианты матриц | Результаты операций | |||
| »А = [1/3 2/3; 4.99 5.01] A = 0.3333 0.6667 4.9900 5.0100 | »fix(A) ans = 0 0 4 5 | »floor(А) ans = 0 0 4 5 | »ceil(A) ans = 1 1 5 6 | |
| »X = [1 23] X = 1 23 | »Y = [–1.6308] Y = –1.6308 | »sign(X) ans = 1 1 | »round(Y) ans = –2 | »rem(X, Y) ans = 1.0000 0.1693 |
Примеры операций приведены в табл. 3.19.
Матричные функции
Весьма представителен в Matlab набор матричных функций:
• expm(X) возвращает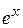 
от матрицы X (табл. 3.20). Комплексный результат получается, если X имеет неположительные собственные значения. Функция expm является встроенной и использует разложение Паде. Ее вариант располагается в виде m-файла «expm1.m». Второй метод вычисления матричной экспоненты использует разложение Тейлора и находится в файле «expm2.m». Реализация третьего способа вычисления матричной экспоненты находится в файле «expm3.m» и использует спектральное разложение матрицы А. Этот метод неудачен, если входная матрица не имеет полного набора
линейно независимых собственных векторов;
Таблица 3.20
| Матрица | Операция | Матрица | Операция |
| »X = [1 2; 4 5] X = 1 2 4 5 | »expm(X) ans = 136.1004 185.0578 370.1155 506.2159 | »X = [1 2;4 5] X = 1 2 4 5 | »[Y, esterr] = funm(X, @sqrt) Y = 0.5373 + 0.5373i 0.7339 – 0.1967i 1.4679 – 0.3933i 2.0052 + 0.1440i esterr = 9.5688e–016 |
• funm(X, @function) возвращает любую функцию от квадратной матрицы X, если правильно ввести имя, составленное из латинских букв. Команды funm(X, @exp), funm(X, @sqrt), funm(X, @log), Hexpm(X), sqrtm(X), logm(X) вычисляют одинаковые функции, но используют соответственно разные алгоритмы. Однако предпочтительнее использовать ехрm(Х), sqrtm(X), logm(X). Операция [Y, esterr] = funm(X, @function) не выдает никакого сообщения, но кроме результата вычислений в матрице Y возвращает грубую оценку относительной погрешности результата вычислений funm в esterr (табл. 3.20). Если матрица X – действительная симметрическая или комплексная эрмитова, то ее форма Шура диагональна и полученный результат может иметь высокую точность;
• logm(X) возвращает логарифм матрицы (табл. 3.21). Результат получается комплексным, если X имеет отрицательные собственные значения; если матрица X – действительная симметрическая или комплексная эрмитова, то теми же свойствами обладает и logm(X). Операция [Y, esterr] = logm(X) не выдает какого-либо предупреждающего сообщения, но возвращает оценку погрешности в виде относительной невязки norm(expm(Y) – X) / norm(X);
Таблица 3.21
| Матрица X | Операция | Матрица X | Операция |
| »X = [1 2;4 5] X = 1 2 4 5 | »Y = logm(X) Y = –0.2110+2.4777i 0.7603–0.9069i 1.5207–1.8138i 1.3097+0.6639i | »X = [1 2;4 5] X = 1 2 4 5 | »Y = sqrtm (X) Y = 0.5373+0.5373i 0.7339–0.1967i 1.4679–0.3933i 2.0052+0.1440i |
• sqrtm(X) возвращает квадратный корень из X, соответствующий неотрицательным действительным частям собственных значений X. Результат получается комплексным, если X имеет отрицательные собственные значения. Если X вырожденная, то выдает предупреждение об ошибке (табл. 3.21). Операция [Y, resnonii] = sqrtm(X) возвращает оценку погрешности в виде относительной невязки по нормам Фробениуса; [Y, alpha, condest] = sqrtm(X) – функция с тремя выходными аргументами, возвращающая помимо квадратного корня фактор стабильности и оценку числа обусловленности результирующей матрицы Y.