Вариационные принципы и проблема критериев
Подход к решению обратных задач геофизики, основанный на принципах квазирешений на аппроксимационно содержательных классах единственности сталкивается не только с проблемами скрытой эквивалентности, обсуждавшимися в предшествующих разделах. Другой весьма существенной проблемой служит проблема параметризациивыбранной аппроксимационной модели, модели наблюдаемой и соответствующего физического поля. Суть вопроса состоит в том, что система параметров наблюдаемой, и система параметров аппроксимационной модели, независимы между собой. В силу удачного стечения обстоятельств или применением специальных приемов обработки они могут оказаться согласованными. Однако изначально - это не связанные между собой параметризации. Параметризация модели наблюдаемой предопределена условиями наблюдения, а параметризация содержательной аппроксимационной модели (конструкции) определена особенностями субъективно выбранной конструкции. На этапе конструирования квазирешения соответствующее уравнение умножается на сопряженный оператор (см. п.3.2), чем достигается согласованием размерности входных и искомых параметров. Однако это технический прием не отражает естественное требование того, чтобы в задаче изначально были согласованы искомые и заданные величины. Сказанное означает, что процесс введения априорной информации об изучаемой модели в виде содержательных аппроксимаций обладает недостатками, является однобоким, не учитывающим весьма важных свойств задачи реконструкции модели среды по физически полям. Эта однобокость проявляется в том, что при таком подходе, возможны ситуации, при которых в сформулированной задаче как теряется информация (не все существенные параметры наблюдаемой активно используются) так и наоборот, делается попытка восстановить параметры при отсутствии соответствующей информации в наблюдаемой. Но самое неприятное состоит в том, что весьма затруднительно до проведения вычислительных процедур по реконструкции параметров модели определить, какая из этих трех ситуаций реализуется: информация теряется; информация согласована; информации недостаточно. Альтернативный использованию аппроксимационно содержательных моделей среды является путь доопределения задачи требованием оптиальности элементов модели среды в своем классе эквивалентности. Приведем пример такого доопределения и, одновременно, проследим основные узловые моменты такого подхода.
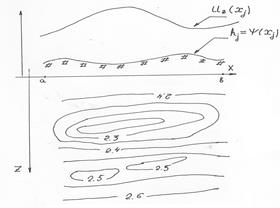
Пусть требуется реконструировать структурную плотностную модель среды по заданному гравитационному полю. Для простоты рассмотрим двухмерную задачу – рис.1. Система из N 
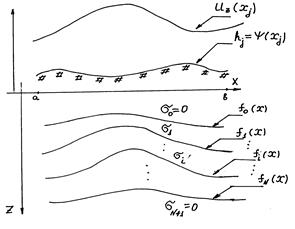пластов с заданными значениями плотности 
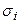ограничена N+1 границей, каждая из которых описывается однозначной функций 
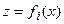. Особенность модели задачи состоит в том, что гравитационное поле 
задано в дискретном множестве точек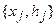 
на рельефе, описываемом функцией 
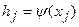. Вне интервала 
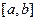границы продолжаются горизонтальными прямыми линиями. Гравитационный эффект зон вне профиля 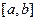в точках 
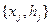рассчитан и равен 
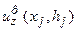. Связь между введенной моделью среды и значениями вертикальной производной гравитационного потенциала в «точках наблюдения» определена условием (см. п.2.1.4):
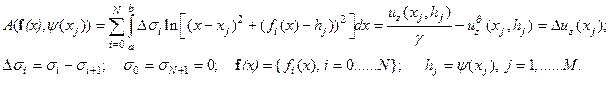 | (5.1) |
Ясно, что такой случай задания поля менее информативен, чем если бы поле было задано всюду на дневной поверхности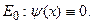 
Оператор (1) в этом, последнем случае записываем 
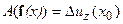. Реконструировать 
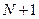функцию 
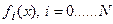по «известной» одной 
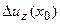- задача явно недоопределенная. Рассмотрим какого сорта информация об изучаемой модели среды, помимо уже введенной – задано число границ и значения плотности между ними, может быть в распоряжении интерпретатора. Прежде всего, обратимся к источнику этой информации. Им, как правило, служат данные бурения, данные других геофизических методов и некоторые общие соображения о генезисе и эволюции изучаемого участка. Бурением вскрыты горизонты и имеется достоверная информация о глубинах залегания границ в этих точках. Проведенная сейсморазведка в других участках характеризовалась различным качеством материала и с разной степенью достоверности на различных участках позволила определить глубина залегания границ. В зонах с хорошим качеством материала (здесь влияет много факторов) достоверность построения выше, с плохим – ниже. В промежуточных между бурением и другими геофизическими результатами, которые лишь корреляционно, косвенно связаны с изучаемыми плотностными границами (которые сами являются определенной идеализацией) использована интерполяция, на основе знания о характерных углах залегания границ, а эта информация почерпнута из геолого-тектонического анализа. Как можно объединить эту разнородную, разноплановую информацию об изучаемой модели среды. Таким объединяющим началом может служить ранжированость. Возможно, считать, что комплекс внешней, априорной информации о глубине залегания границы с номером 
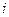в точке 
в принципе позволяет ранжировать возможные глубины залегания границ - указать систему предпочтений – на каких глубинах более вероятно, а на каких менее нахождение этой границы. Подчеркнем, что речь идет о выделенной точке профиля и глубинах залегания конкретной границы в этой точке (рис. 2). Таким образом можно предположить, что для каждой точки профиля возможные глубины залегания границ образуют вполне упорядоченное множество: для каждых двух произвольно взятых глубин можно указать какая из них более предпочтительна или они имеют одинаковый ранг – в том числе ранг недопустимой глубины (например, на дневной поверхности или выше нее). Такой ранжировке может быть поставлено в соответствие распределение вероятности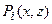 
, которое для выделенной точки определяет вероятность того (плотность вероятности), что граница с номером 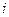в этой точке залегает на глубине 
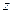. Пока не следует утруждать себя выработкой техники ранжирования и конструированием вероятностных законов. Это будет достаточно унифицировано в дальнейшем. В настоящем разделе речь идет об иллюстрации принципиальных позиций. Важно то, что такая вероятность может быть сконструирована как исчерпывающее выражение всего комплекса данных о возможной отнесенных к информации о глубине залегания границы в данной точке. Для того чтобы перейти от вероятности в точке профиля к вероятности границы целиком, следует проинтегрировать вероятностный закон 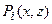по . Таким образом, для произвольного «претендента» на функцию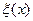 
, описывающую положение границы с номером 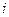можно вычислить интегрированную вероятность – достоверность, ранг этого претендента: 
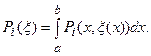Однако реально имеются
|
границах. Это значить, что он должен быть многомерным. Конкретно - мерным. Следовательно, существует функция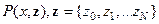 
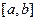, которая для каждой точки профиля и 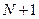значений 
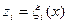оценивает вероятность того, что все граница залегают на глубинах 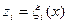. Граница с номером 0 залегает на глубине 
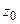, граница с номером 1 на глубине 
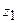, граница с номером 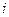на глубине 
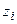. Для того, чтобы перейти от вероятности в точке профиля к вероятности системы границ целиком, следует проинтегрировать вероятностный закон 
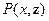по . То, что в результате получиться, называется функцией правдоподобия. Таким образом, для произвольного «претендента» на систему из 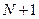функцию 
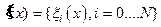, описывающую положение всех границ можно вычислить интегрированную вероятность – достоверность, ранг этого претендента – его правдоподобие:  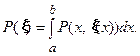| (5.2) |
Задачу реконструкции структурной плотностной модели (1) можно доопределить требованием:
 |
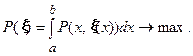Это означает, что среди всех эквивалентных по гравитационному эффекту с учетом условий задания поля систем границ следует выбрать ту единственную систему, которая наиболее вероятна, с точки зрения имеющейся априорной информации, выраженной в виде принятого вероятностного закона. Вероятностный закон (2) служит своего рода вместилищем априорной разнородной информации. Таким образом, мы приходим к задаче:
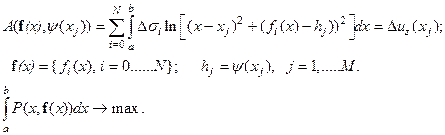 | (5.3) |
Функционал (2) называется критерием оптимальностии постановка (3) соответствует нахождению того единственного элемента из класса эквивалентных по гравитационному полю, который оптимален относительно введенного критерия оптимальности.
Постановку (3) можно пояснить и несколько по иному. Система уравнений в (3) не может быть однозначно решена относительно искомых границ. Поэтому вместо попыток решить эту задачу переходим к другой – задаче минимизации заданного критерия. Что же касается уравнений, то они рассматриваются как дополнительные условия к этой задаче минимизации.
Для дальнейшей иллюстрации примем для простоты, что глубины залегания границ независимы между собой. В этом случае имеются (могут быть сконструированы) 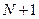функци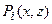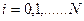и 
и 
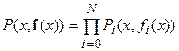. Еще одно упрощение состоит в том, что вероятностные законы примем нормальными так, что 
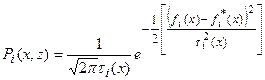. Здесь 
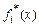- оценка среднего значения, оценка стандарта – среднеквадратичного уклонения. Тогда:
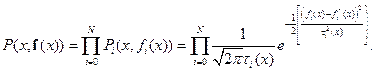 | (5.4) |
Величины 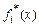имеют смысл оценок среднего для возможных глубин залегания границы или нулевого приближенияк глубине залегания. 
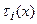априорная оценка среднеквадратичной погрешности построения нулевого приближения. Нетрудно понять, что максимизация выражения:
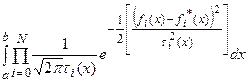эквивалентна минимизации:
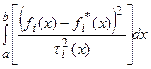, и задача (3) приобретает более частный вид:
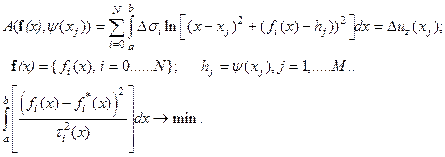 | (5.5) (5.6) |
Это задача на условный минимум, в которой условиями служат 
уравнений, обеспечивающие требование того, чтобы все сравниваемые по критерию оптимальности (6) границы принадлежали одному классу эквивалентности с учетом параметризации наблюдаемых компонент гравитационного поля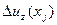 
. Для ее решения воспользуемся принципом Лагранжа (см. прил.2.6), в соответствии с которым должны найтись числа 
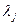, такие, что экстремаль задачи (5-6) на условный минимум совпадает с экстремалью задачи на безусловный минимум:
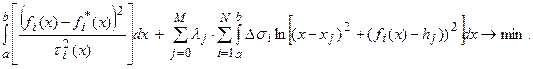 | (5.7) |
Применимость принципа Лагранжа требует, чтобы оператор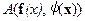 
, определенный в (5), был непрерывно дифференцируем, а его производная (Фреше) регулярна в окрестности точки экстремума – решения 
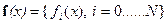задачи (7). Производная этого оператора имеет вид:
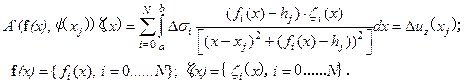 | (5.8) |
Она представляет собой линейный непрерывный оператор из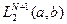 
в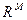 
и отображает функцию 
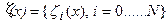в набор значений имеющий параметризацию наблюдаемой. Его непрерывная дифференцируемость очевидна, а что касается регулярности, то это более тонкое свойство, которое будет обсуждаться ниже. Пока мы будем предполагать регулярность этого оператора. Варьируя (7) в предположении его экстремума получим уравнение Эйлера как необходимое условие минимума:
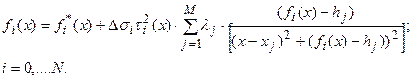 | (5.9) |
Это система ровно из такого числа уравнений, сколько искомых границ. Эти уравнения доопределяют систему (1). Уравнения (9) служат не чем иным как параметризацией искомых границ, параметры которой согласованы с параметризацией наблюдаемой. Их столько же и они определены в тех же точках, в которых задана наблюдаемая. Система из M уравнений (1) служит для того, чтобы определить эти параметры, которых ровно столько же, сколько и чисел 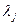, после чего все 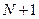границы находятся из (9). Таким образом, введение критерия оптимальности доопределяет исходно неопределенную задачу, обеспечивает описание класса единственности за счет формирования параметризации, согласованной с наблюдаемой, причем делает это автоматически и параметризация выражает оптимальный принцип отбора из класса эквивалентности, основанный на выражении априорной информации о среде. Меняя нулевые приближения и оценки среднеквадратичной погрешности в представлении (9) можно «настроить» класс единственности (9) на заданный элемент. Эти параметры - 
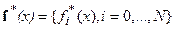и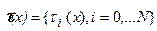 
служат «рулями», позволяющими осуществлять «навигацию по классам эквивалентности» до получения наилучшего решения. Теперь, после того, как формирование класса единственности завершено следует найти решение уравнения (1) на множестве, имеющем представление (9). Делать это необходимо с учетом приближенности исходных данных и последняя задача – традиционна для уже рассмотренных методов решения некорректных задач. В частности можно воспользоваться приемами итерационной регуляризации, сконструировав следующий итерационный процесс для решения (1) на множестве (9):
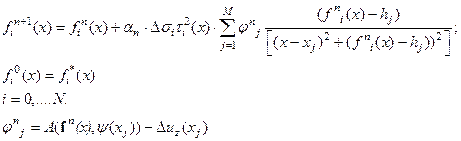 | (5.10) |
Далее будет показано, что если оператор (8) регулярен, то существует такая последовательность чисел 
, называемых параметром релаксации, что процесс (10) монотонно сходится к решению задачи (1,9). Подведем некоторые итоги. Введение вариационного принципа позволило сформировать критерий оптимальности, выражающий унифицированным образом разнородную и разноточную информацию об изучаемом объекте, построить экстремальный класс(9) параметризующий класс единственности, оптимальный для сформированного критерия и согласованный с параметризаций наблюдаемой. Полученый результат конструктивен, поскольку указан способ выделения единственного элемента, отвечающего конкретной наблюдаемой на построенном экстремальном классе. Априорная информация концентрирована в виде критерия оптимальности (6) и включает в себя нулевое приближение и оценки среднеквадратичной погрешности его построения -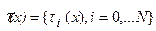 
. Ее можно легко менять, управляя свойствами получаемого результата, не меняя технологической схемы построения решения и, тем самым оперативно уточнять и подстраивать параметры критерия оптимальности.
Приведенная схема анализа и решения недоопределенных обратных задач геофизики несомненно является преимущественной в сравнении с методами построения квазирешений на аппроксимационно содержательных классах. Однако есть одно обстоятельство, которое требует особых исследований в описанном подходе. Оно образно может быть выражено следующим тезисом: «рули должны работать правильно». В приведенных рассуждениях этими рулями служит критерий оптимальности и входящие в его конструкцию нулевые приближения 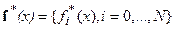и оценки погрешности их построения 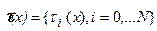. Из соотношения (9) нетрудно видеть, что величины 
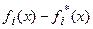в правой части (9) при 
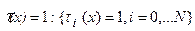, резко убывают по мере возрастания 
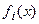. Точнее говоря, если оператор 
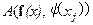регулярен как в окрестности 
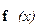, что предполагается, так и в окрестности 
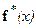, что также, как правило, выполнено, то для любой последовательности чисел 
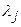в (9) найдется такая последовательность чисел 
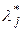, что:
.
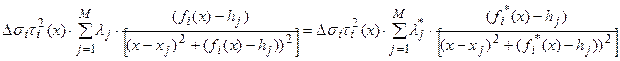Тогда (9) перепишется:
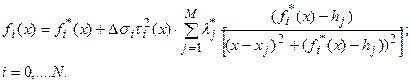
Таким образом, по мере перехода к более глубоко залегающим границам – увеличению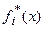 
при равной достоверности построения всех компонент нулевого приближения 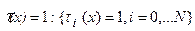отличие в получаемых границах от нулевого приближения будет резко убывать. Таким образом, разноглубинные компоненты модели ведут себя по-разному, а это не было заложено в критерии оптимальности. Это обстоятельство хорошо становиться понятным, если заметить, что величины:
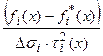
есть краевые значения на искомых границах одной и той же гармонической функции:
,
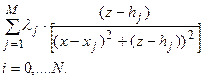резко убывающей с возрастанием . Это проявление внутренних свойств рассматриваемой задачи. Интуитивно ожидается, что равнодостоверные компоненты модели по мере согласования с полем должны и равноварьироваться. Следовательно, результат решения в (10) ведет себя по своим свойствам, не так как это ожидается от критерия, что объясняется вышеописанными внутренними свойствами задачи. Это также своего рода проявление скрытой эквивалентности, как и в методах использующих аппроксимационно содержательные модельные классы за тем лишь существенным исключением, что здесь эти эффекты прослеживаемы и управляемы. Следует изучить эти эффекты и, тем самым, выработать адекватные правила формирования критерия оптимальности, свойства получаемых решений.
Для того чтобы выявить суть проблемы еще более рельефно, рассмотрим другую частную задачу - реконструкции плотностного распределенияв заданной области, используя принципы отбора оптимального решения аналогичные выше использованным. Для простоты также ограничимся плоской задачей.
В области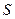 
нижнего полупространства распределены массы с плотностью 
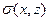(рис.3). Как и в предшествующем случае, поле заданно в точках 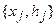на рельефе, описываемом функцией 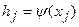. Связь распределения плотности и вертикальной производной гравитационного потенциала будет иметь вид (см.п.2.2)
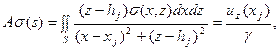 | (5.11) |
Считая, что в каждой точке 
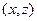области 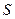задано нулевое приближение 
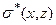и отклонение значений в этой точке нулевого приближения от искомого распределения есть нормально распределенная величина с нулевым средним и оценкой среднеквадратичной погрешности равной в этой точке величине 
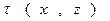приходим к критерию оптимальности, эквивалентному максимуму правдоподобия:
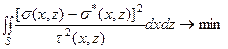 . | (5.12) |
Также как и в (5-7) задача (11-12) суть вариационная задача на условный минимум, в которой условиями служат уравнений. Они обеспечивают требование того, чтобы все сравниваемые по критерию оптимальности (12) плотностные распределения принадлежали одному классу эквивалентности. Как раз тому, который соответствует наблюдаемым компонентам гравитационного поля 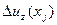. Для ее решения, как и выше, воспользуемся принципом Лагранжа. В соответствии с ним должны найтись числа 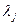, такие, что экстремаль задачи (5-6) на условный минимум совпадает с экстремалью задачи на безусловный минимум:
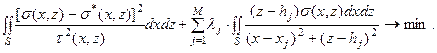 | (5.13) |
Необходимым и достаточным условием тому, чтобы распределение плотности 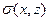было решением этой задачи служит (см. прил.2.6) .
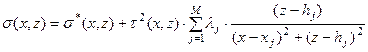 . | (5.14) |
(14) это просто уравнение Эйлера для (13), также как (9) это уравнение Эйлера для (7). Но в отличие от рассмотренной выше задачи (13) это необходимые и достаточные условия. Это связано с линейностью и ограниченностью оператора (11). В него входят параметры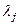 
, которых ровно столько, сколько уравнений в (11). Подстановка (14) в (11) позволяет однозначно найти эти параметры, после чего из (14) однозначно вычисляется искомое распределение плотности. Таким образом, (14) это согласованная с характером задания –наблюдаемой параметризация модели среды, следующая из введенного критерия оптимальности. Как и выше введение критерия оптимальности доопределяет исходно неопределенную задачу, обеспечивает описание класса единственности за счет формирования параметризации, согласованной с наблюдаемой, причем делает это автоматически и параметризация выражает оптимальный принцип отбора из класса эквивалентности, основанный на выражении априорной информации о среде.
Легко заметить особые аналитические свойства, присущие решению вида (14). Если предположить, что нулевое приближение 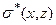к искомой плотностной модели построено равно достоверно во всех точках области 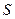, то это означает что 
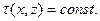Тогда величина уклонения искомого решения от нулевого приближения оказывается гармонической функцией:
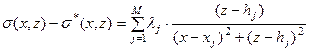 | (15) |
.
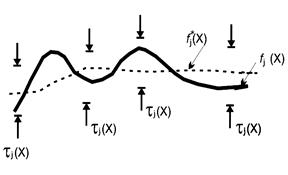
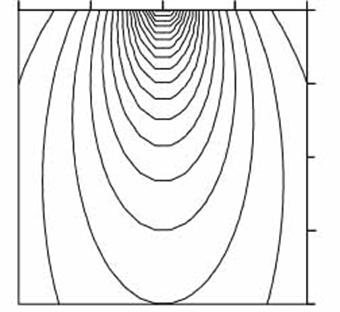Такое специальное свойство получаемого решения ведет к заключению о том, что это формально эквивалентная модель. Это расходится с ожиданиями того, что в условиях «равноточности» исходных построений для разных глубин следует ожидать «равноуклонения» от нулевого приближения на тех же глубинах. Этого не происходит. Типичный график гармонической функции приведен на рис.4 и наглядно демонстрирует это обстоятельство. В предположении равенства нулю нулевого приближения именно такого сорта распределения следует ожидать в качестве решений наименее уклоняющихся от нуля.
Свойства гармонических функций таковы, что получение некоторых внутренних локализаций невозможно. Таким образом, критерии максимальной близости в смысле наименьших квадратов не соответствуют по свойствам получаемых решений ожиданиям в получении некоторых небольших содержательных поправок к известному нулевому приближению. Причин этому много. Их можно найти, например, в том, что значения и глубин залегания границ, и значения плотностей в разных точках не являются независимыми, и потому интегральный критерий максимума правдоподобия должен быть видоизменен.
Сказанное позволяет сделать выводы.
1. Введение критериев оптимальности позволяет доопределить исходно недоопределенные задачи и выработать классы оптимальных моделей, которые называются экстремальными классами, параметризованные согласовано с параметризацией моделей.
2. Экстремальные классыявляются максимально широкими классами единственности для конкретной параметризации наблюдаемой в том смысле, что используют все значения наблюдаемой.
3. Параметры – нулевое приближениеи оценка достоверности его построения входящие в квадратичный критерий оптимальности (6) и (12) позволяют «настроить» экстремальный класс на требуемые свойства решений.
4. Необходимо исследование свойств экстремальных классов для правильной методики формирования параметров критериев оптимальности. Здесь следует понимать, что значение имеют не кажущаяся убедительность аргументов в пользу выбора того либо иного критерия оптимальности – его управляющих параметров, а соответствие результатов параметрам, заложенным в критериях. Только так можно перейти к получению содержательных а не эффективных – формально эквивалентных моделей. Управляющие параметры - рули должны работать предсказуемо.