Математика и загадка тяготения

Причину же этих свойств силы тяжести я до сих пор не мог вывести из явлений, гипотез же я не измышляю… Довольно того, что тяготение на самом деле существует и действует согласно изложенным нами законам и вполне достаточно для объяснения всех движений небесных тел и моря.{5}

Ньютон

В 1642 г., в год смерти Галилея, на ферме близ небольшой английской деревушки, у одной незадолго до того овдовевшей женщины родился недоношенный ребенок. Несмотря на столь неблагоприятные обстоятельства рождения и здоровье, столь слабое, что мать всерьез опасалась за жизнь ребенка, Исаак Ньютон (1642‑1727) дожил до восьмидесяти пяти лет и снискал славу одного из величайших представителей рода человеческого. Как мы увидим в дальнейшем, Ньютон в своей работе по существу следовал методологии Галилея, продолжая и развивая ее. Как заметил однажды Алфред Норт Уайтхед, «Галилей знаменует первый приступ, Ньютон – окончательную победу».

Если не считать ярко выраженного интереса к механическим устройствам, Ньютон не подавал особых надежд в юности. Поскольку он не проявлял никакого интереса к сельскому хозяйству, мать отправила его в Кембридж, и в 1661 г. он поступил в Тринити‑колледж (колледж св. Троицы). Хотя пребывание в стенах прославленного колледжа давало его воспитанникам определенные преимущества, например возможность изучать труды Декарта, Коперника, Кеплера, Галилея или слушать лекции знаменитого математика Исаака Барроу, Ньютон, насколько можно судить, извлек немного пользы из учебы. Он был слаб в геометрии и даже подумывал заняться изучением права вместо натурфилософии. Четыре года обучения завершились столь же незаметно, как и начались.

В год, когда Ньютон окончил колледж в Лондоне, в его округе разразилась эпидемия чумы. Кембриджский университет был закрыт. Ньютону не оставалось ничего другого, как уединиться в тиши родительского дома в Вулсторпе, где он провел безвыездно 1665‑1666 гг. В этот период он начал свои работы по механике, математике и оптике, завершившиеся триумфальным успехом. Ньютон осознал, что открытый им закон всемирного тяготения дает ключ ко всей механике; он разработал также общий метод решения задач математического анализа и, проведя серию экспериментов, совершил эпохальное открытие, установив, что белый солнечный свет включает в себя все цвета радуги от красного до фиолетового. Сам Ньютон‑впоследствии так охарактеризовал этот период: «Я был в то время в расцвете моих изобретательских сил и думал о математике и философии больше, чем когда‑либо после» ([20], с. 31‑32).

В 1667 г. Ньютон возвратился в Кембридж, где был избран членом совета Тринити‑колледжа. В 1669 г. Исаак Барроу оставил свой пост главы кафедры математики, целиком посвятив себя теологии, и Ньютон занял его место. Судя по всему, Ньютон не был хорошим преподавателем. Очень немногие студенты посещали его лекцйи, и никто не отмечал особой оригинальности в его преподавании.

В 1684 г. по настоянию своего друга Эдмонда Галлея (1656‑1742), астронома, в честь которого названа комета (комета Галлея), Ньютон занялся подготовкой к публикации своей работы по тяготению. Галлей взял на себя редактирование первого издания и значительную часть издержек. В 1687 г. классическое произведение Ньютона «Математические начала натуральной философии» (часто называемое для краткости просто «Начала») вышло из печати.

После этой публикации имя Ньютона обрело широкую известность. При его жизни «Начала» выдержали три издания. Появились и популярные изложения этого труда. Популяризация и в самом деле была необходима, так как «Начала» весьма трудны для чтения и далеко не все в этом сочинении понятно непосвященному, хотя издатели неоднократно утверждали обратное. Почти сто лет понадобилось величайшим математикам, чтобы довести до полной ясности ньютоновские «Начала».

Ньютон воздавал должное своим предшественникам и не придавал полученным результатам особенно большого значения. На склоне лет он сказал своему племяннику:

Не знаю, кем я кажусь миру, но самого себя я вижу всего лишь мальчиком, играющим на берегу океана, который забавляется, подбирая то обкатанный камешек, то красивую раковину, в то время как необъятный океан истины простирается передо мною, уходя в неведомые дали.

Из великих свершений, достигнутых Ньютоном в молодые годы, для нас наибольший интерес представляют его философия науки и работа над законом всемирного тяготения. Философия Ньютона содержала в еще более явном виде ту программу физических исследований, начало которой было положено еще Галилеем: законы природы, описывающие наблюдаемые явления на точном языке математики, надлежит формулировать, согласуясь с воспроизводимыми и допускающими экспериментальную проверку явлениями. Из этих законов путем математических рассуждений следует выводить новые законы. Подобно Галилею, Ньютон хотел знать, по какому плану Создатель сотворил мир, но опасался, что за многочисленными явлениями не сможет различить четкий механизм.

В предисловии к первому изданию «Начал» Ньютон говорит следующее:

Так как древние, по словам Паппуса, придавали большое значение механике при изучении природы, то новейшие авторы, отбросив субстанции и скрытые свойства, стараются подчинить явления природы законам математики.

В этом сочинении имеется в виду тщательное развитие приложений математики к физике… поэтому и сочинение это нами предлагается как математические основания физики. Вся трудность физики, как будет видно, состоит в том, чтобы по явлениям движения распознать силы природы, а затем по этим силам объяснить остальные явления. Для этой цели предназначены общие предложения, изложенные в книгах первой и второй.

([19], с. 1‑3.)

Математические начала были для Ньютона, как и для Галилея, началами количественными. Расположить все в ясном и четком порядке по «мере, числу и весу» – такую задачу ставил перед собой Ньютон в своем сочинении.

Если говорить об описании природы, то величайшей заслугой Ньютона с полным основанием можно считать открытие единых законов, – управляющих движениями тел на небе и на Земле. Галилей наблюдал небесные тела, как никто ранее, но его успехи в математическом описании природы ограничивались описанием движений, происходящих либо по поверхности Земли, либо вблизи нее. Еще при жизни Галилея его современник Кеплер вывел три знаменитых закона движения планет, упростив тем самым гелиоцентрическую теорию. Но две области физики – земная и небесная – казались совершенно независимыми. Найти какую‑нибудь связь между земными и небесными явлениями – такая задача будоражила умы великих ученых. И величайший из них справился с этой задачей.

Были все основания считать, что какой‑то принцип, общий для земных и небесных явлений, все же существует. Согласно первому закону движения Галилея, о котором Ньютон мог узнать из сочинений Декарта или самого Галилея, чьи труды Ньютон оценивал высоко, тела должны двигаться равномерно и прямолинейно до тех пор, пока их движение не нарушали приложенные извне силы. Следовательно, планеты, однажды приведенные каким‑то образом в движение, должны далее двигаться равномерно и прямолинейно, между тем как, согласно законам Кеплера, они обращаются вокруг Солнца по эллипсам. Значит, должна существовать какая‑то сила, вынуждающая планеты постоянно отклоняться от прямолинейной траектории, подобно тому как груз, раскачивающийся на конце нити, не улетает по прямой, поскольку рука, держащая другой конец нити, притягивает его. Естественно допустить, что на планеты действует сила притяжения со стороны Солнца. Во времена Ньютона физикам было известно также, что Земля притягивает находящиеся на ней тела. А так как и Земля, и Солнце притягивают тела, была выдвинута и широко обсуждалась еще во времена Декарта идея объединить оба вида притяжения в рамках одной теории.

Ньютон превратил общие соображения в четко поставленную математическую задачу и, не вдаваясь в выяснение физической природы силы притяжения, решил эту задачу с помощью им же разработанного блестящего математического метода. Бытует легенда, что мысль о тождестве земного и солнечного притяжения осенила Ньютона, когда он обратил внимание на падение яблока с ветки дерева. Математик Карл Фридрих Гаусс заметил как‑то, что эту историю Ньютон, должно быть, придумал сам, желая отделаться от глупцов, надоевших ему расспросами о том, как он открыл закон всемирного тяготения; однако, согласно другим источникам, легенда имеет под собой основания. Как бы то ни было, яблоко, упавшее на глазах у Ньютона (в отличие от другого яблока, сыгравшего заметную роль в истории!), способствовало подъему человеческого знания еще на одну ступень.

Ньютон начал свое исследование с рассмотрения задачи о теле, брошенном в горизонтальном направлении с вершины горы. Эту задачу решил еще Галилей, который показал, что такое тело при движении описывает параболу. Чем выше начальная скорость, тем более «широкой» и пологой становится парабола и тем дальше улетает тело. Но Галилей рассматривал тела, бросаемые не слишком далеко, что позволяло ему пренебречь кривизной Земли. Ньютону первому пришла в голову мысль рассмотреть полет тела, брошенного в горизонтальном направлении со скоростью, при которой становилась существенной кривизна Земли (тело описывает траекторию VD; рис. 26).

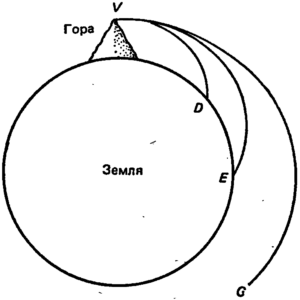
Рис. 26.

Не улетит ли такое тело в космическое пространство и не покинет ли Землю навсегда? Нет, ибо Земля продолжает его притягивать. В каком направлении действует на тело земное тяготение? Галилей всегда считал, что сила тяжести действует на тела вниз по вертикали, но для тела, движущегося по околоземной орбите, «вертикально вниз» означает «к центру Земли». Итак, если тело бросить с вершины горы, то оно будет притягиваться к Земле. Если увеличить начальную скорость, то тело улетит несколько дальше, описав траекторию VE, а при достаточно большой начальной скорости может даже стать искусственным спутником Земли и обращаться вокруг нее (если бы не было сопротивления воздуха) неограниченно долго. Вот что пишет об этом Ньютон в своих «Началах»:

Подобно тому как брошенное тело может быть отклонено силою тяжести так, чтобы описывать орбиту вокруг Земли, так и Луна или силою тяжести, или же иною силою, которая влечет ее к Земле, может быть отклоняема от прямолинейного пути и вынуждена обращаться по своей орбите; без такой силы Луна не могла бы удерживаться на своей орбите.

([19], с. 27.)

Но коль скоро Земля силой своего тяготения может заставить Луну обращаться вокруг нее, то и Солнце силой своего тяготения могло бы заставить планеты обращаться вокруг него. Поэтому у Ньютона были некоторые основания надеяться на успех дерзкого замысла: доказать, что та же самая сила, которая притягивает тела к Земле, заставляет Луну обращаться вокруг Земли и планеты вокруг Солнца.

Все рассуждения Ньютона, о которых мы упоминали до сих пор, были чисто качественными и умозрительными. И чтобы сделать решительный шаг вперед, необходимо было придать им количественный характер. Продолжая рассуждать о действующей на Луну силе земного притяжения, Ньютон пишет дальше:

Если бы эта сила была меньше соответствующей этой орбите, то отклоняла бы Луну от прямолинейного пути недостаточно, а если больше, то она отклоняла бы ее больше, чем следует, и приблизила бы ее от орбиты к Земле. Следовательно, надо, чтобы эта сила была в точности надлежащей величины. Дело математиков найти такую силу, которая в точности удерживала бы заданное тело в движении по заданной орбите с данной скоростью, и наоборот, найти тот криволинейный путь, на который заданною силою будет отклонено тело, вышедшее из заданного места с заданной скоростью.

([19], с. 27.)

Рассуждение Ньютона, с помощью которого он показывает, что одна и та же формула применима и к земным, и к небесным телам, ныне считается классическим. Мы приведем здесь его в несколько упрощенном виде, который тем не менее правильно передает самую суть. Орбиту Луны приближенно можно считать окружностью. Так как Луна (рис. 27) движется не по прямой MP , ее, очевидно, притягивает к Земле какая‑то сила. Если MP – расстояние, которое Луна проходит за 1 с в отсутствие силы тяготения, то РМ' – расстояние, на которое Луна смещается к Земле за ту же секунду под действием силы тяготения. Ньютон принял расстояние РМ' за меру силы, с которой Земля притягивает Луну. Соответствующая величина для тела, находящегося вблизи поверхности Земли, составляет примерно 9,8 м; если тело выпустить из рук, то под действием земного тяготения оно за первую секунду пройдет расстояние, равное 9,8 м. Ньютон вознамерился показать, что одна и та же сила заставляет Луну проходить за 1 с расстояние РМ' а тело вблизи поверхности Земли пролетать в свободном падении 9,8 м.

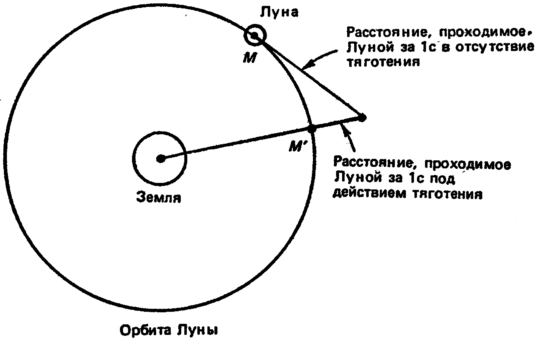
Рис. 27.

Приближенные оценки привели его к мысли, что сила притяжения между телами зависит от квадрата расстояния между центрами тел и что с увеличением расстояния эта сила убывает. Расстояние между центром Луны и центром Земли примерно в 60 раз больше радиуса Земли. Следовательно, на Луну Земля действует в 60² раз слабее, чем на тело, находящееся вблизи земной поверхности, т.е. сила действия Земли на Луну составляет 1/(60)² от той силы, с которой она притягивает земные тела. Но это означает, что под действием земного притяжения Луна должна приближаться к Земле за 1 с на расстояние, равное 9,8/(60)²= 0,0027 м. Произведя некоторые численные тригонометрические расчеты, Ньютон обнаружил, что Луна действительно притягивается Землей силой «в точности надлежащей величины». Тем самым он получил весьма убедительное подтверждение своей гипотезы: все тела в мире притягиваются друг к другу по одному и тому же закону.

Более тщательные исследования Ньютона показали, что сила тяготения, действующая между любыми двумя телами, определяется формулой

F = kMm /r ², (1)

где F – сила тяготения, M и m – массы тел, r – расстояние между ними, коэффициент k одинаков для всех тел. Например, M может означать массу Земли, m – массу какого‑либо тела, находящегося вблизи поверхности Земли. В этом случае r – расстояние от центра Земли до тела. Формула (1) выражает закон тяготения.

Чтобы подвести прочную основу под все свое грандиозное исследование земных и небесных движений, Ньютон сформулировал в своих «Началах» три закона движения, известные ныне как законы Ньютона (хотя первые два закона были сформулированы еще Декартом и Галилеем). Первый закон Ньютона:

Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменять это состояние.

([19], с. 39.)

Второй закон Ньютона:

Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

([19], с. 40.)

Результирующую всех действующих на тело сил можно представить в виде произведения массы тела на ускорение, создаваемое этой силой:

F = ma.

Ускорение характеризует увеличение или уменьшение скорости тела либо изменение ее направления. (Математически F и a – векторы.)

Третий закон Ньютона:

Действию всегда есть равное и противоположное противодействие, иначе – взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны.

([19], с. 41.)

К этим трем законам Ньютон добавил закон всемирного тяготения (1). Применительно к движениям планет этот закон был открыт Робертом Гуком, но Ньютон обобщил его и возвел в ранг универсального закона, применимого ко всем телам во Вселенной.

Получив некоторые подтверждения справедливости закона всемирного тяготения, Ньютон показал далее, что этот закон применим к движениям на поверхности Земли или вблизи нее. И здесь ему помогли труды Галилея. Перейдем на язык формул. Пусть M – масса Земли, m – масса тела, находящегося вблизи земной поверхности. Записав формулу (1) в виде F = kMm/r² и разделив обе части на m , получим

F /m = kM /r ². (2)

Независимо от того, какое тело вблизи поверхности Земли мы рассматриваем, величины, входящие в правую часть формулы (2), остаются неизменными, так как r – радиус Земли (~6400 км), M – масса Земли, а постоянная k одинакова для всех тел.

Но второй закон Ньютона утверждает, что любая сила, действующая на тело массой m , сообщает этому телу ускорение. В частности, сила притяжения Земли, действующая на тело, также сообщает ему ускорение. Из второго закона Ньютона следует, что любая сила F связана с вызванным ею ускорением соотношением F = ma , или

F/m = a . (3)

Следовательно, если сила F в формуле (2) есть сила земного тяготения, то правые части формул (2) и (3) можно приравнять, так как левые части равны. В результате получаем

а = kM /r ².

Это соотношение означает, что ускорение, сообщаемое телу силой земного тяготения, всегда равно kM/r² . Поскольку k – постоянная, M – масса Земли, r – расстояние от тела до центра Земли, величина kM/r² одинакова для всех тел, находящихся вблизи поверхности Земли. Следовательно, все тела вблизи поверхности Земли падают с одинаковым ускорением. Именно к такому выводу пришел на основании своих опытов Галилей. Более того, опираясь на этот результат, Галилей математически доказал, что все тела, падающие с одинаковой высоты, достигают поверхности Земли за одно и то же время. Ускорение свободного падения, которое принято обозначать буквой g , легко измерить: оно равно 9,8 м/с².

Несколько уклоняясь от нашей главной темы, заметим, что, согласно третьему закону Ньютона, для каждой силы (действия) всегда существует равная по величине и противоположно, направленная сила (противодействие). Следовательно, если Солнце действует на Землю с силой, удерживающей нашу планету на ее околосолнечной орбите, то Земля в свою очередь должна действовать на Солнце с равной по величине и противоположной по направлению силой. Значит, Солнце под действием этой силы должно двигаться, между тем оно покоится! Разгадку этого «парадоксу» дают несложные вычисления, подобные проделанным Ньютоном. Если m – масса Земли, M – масса Солнца, то сила взаимного притяжения между ними равна

F = kMm /r ².

Земля притягивает Солнце с силой

F = Ma .

Сравнивая эти две формулы, получаем

F/M = km /r ² и F/M = a .

Следовательно, ускорение, сообщаемое Землей любому телу, равно

a = km /r ²,

где m – масса Земли, r – расстояние от центра Земли до тела. Так как масса Земли, гораздо меньше массы Солнца, ускорение, сообщаемое Землей Солнцу, во много раз меньше ускорения, сообщаемого Солнцем Земле. Под воздействием притяжения со стороны Земли и других планет Солнце приходит в движение, но последнее столь слабо, что им можно пренебречь. Из приведенных расчетов следует еще один вывод. Согласно третьему закону Ньютона, Земля притягивает нас с такой же силой, с какой мы притягиваем ее. Но мы падаем на Землю, тогда как «падение» Земли на нас пренебрежимо мало.

Таким образом, вклад Ньютона в теорию тяготения по существу сводится к следующему. Исследуя движение Луны, он пришел к правильной формулировке закона всемирного тяготения. Затем Ньютон показал, что этот закон вкупе с двумя первыми законами движения достаточен для описания движения тел на поверхности Земли. Тем самым Ньютону удалось достичь одной из главных целей программы Галилея, ибо он показал, что законы движения и закон всемирного тяготения принадлежат к числу фундаментальных принципов. Подобно аксиомам Евклида, эти законы служат логической основой для получения других физически значимых законов. Можно представить, каким триумфом явился вывод законов движения небесных тел.

Этот триумф также связан с именем Ньютона. Построив цепочку безукоризненных дедуктивных умозаключений, он показал, что все три закона движения планет, полученные Кеплером, следуют из двух первых законов движения и закона всемирного тяготения.

Из этих законов вытекает важное следствие, которое о многом должно говорить читателю, пытающемуся найти рациональное объяснение эффективности математического метода в познании. Основная ценность законов Ньютона заключается в том, что они, как мы только что видели, применимы к множеству самых разнообразных как небесных, так и земных явлений. Одни и те же количественные соотношения воплощают в себе общие, универсальные характеристики. Следовательно, знание этих формул действительно можно рассматривать как знание описываемых ими явлений.

Работы Галилея и Ньютона ознаменовали начало научной программы физических исследований. Сам Ньютон в предисловии к первому изданию «Математических начал натуральной философии», классическому научному труду, охватившему все, что было сделано Ньютоном в его молодые годы, сформулировал эту программу следующим образом:

Поэтому и сочинение это предлагается нами как математические основания физики. Вся трудность физики, как будет видно, состоит в том, чтобы по явлениям движения распознать силы природы, а затем по этим силам объяснить остальные явления. Для этой цели предназначены общие предложения, изложенные в книгах первой и второй. В третьей же книге мы даем пример вышеупомянутого приложения, объясняя систему мира, ибо здесь из небесных явлений при помощи предложений, доказанных в предыдущих книгах, математически выводятся силы тяготения тел к Солнцу и отдельным планетам. Затем по этим силам также при помощи математических предложений выводятся движения планет, комет, Луны и моря. Было бы желательно вывести из начал механики и остальные явления природы, рассуждая подобным же образом, ибо многое заставляет меня предполагать, что все эти явления обусловливаются некоторыми силами, с которыми частицы тел вследствие причин покуда неизвестных или стремятся друг к другу и сцепляются в правильные фигуры, или же взаимно отталкиваются и удаляются друг от друга.

([19], с. 3.)

С неуклонностью камня, скатывающегося с крутого склона, Ньютон подводил все новые обоснования под математические начала физики и выводил из них следствия. Рассуждая примерно так же, как было описано нами выше, он вычислил массу Солнца и мог вычислять массу любой планеты с ее спутниками. Применив понятие центробежной силы к суточному вращению Земли вокруг собственной оси, Ньютон оценил величину экваториального «выпучивания» Земли и обусловленное им изменение веса тела при перемещении из одной точки земной поверхности в другую. По известным из наблюдений отклонениям формы некоторых планет от сферической Ньютон определил периоды их вращения вокруг собственных осей. Он показал, что морские приливы связаны с гравитационным притяжением Земли Солнцем и Луной.

Однако ряд отклонений в движениях планет ему объяснить так и не удалось. Например, хотя Луна постоянно обращена к Земле одной и той же стороной, периодически становятся видимыми то большие, то меньшие области ее обратной стороны, примыкающие к краю видимого диска. Благодаря возросшей точности наблюдений удалось обнаружить, что продолжительность среднего лунного месяца увеличивается примерно на одну тридцатую секунды за столетие. (Точности такого порядка стремились достигнуть и в наблюдениях, и в теории.) Были замечены и небольшие изменения в эксцентриситетах планетных орбит.

Ньютон хорошо знал о многих из этих отклонений и в своих исследованиях не обошел вниманием теорию движения Луны. Во времена Ньютона положение Луны, наблюдаемое с борта находящегося в открытом море судна, служило для определения долготы. (Морской хронометр, позволяющий точно отсчитывать время при сильном волнении моря, тогда еще не был изобретен.) В своих занятиях лунной астрономией Ньютон не упускал из виду и ее практическое приложение. Луна движется по эллиптической орбите так, что в чем‑то напоминает нетрезвого человека, тщетно пытающегося идти прямо: она то ускоряет, то замедляет свой ход и раскачивается из стороны в сторону. Ньютон был убежден, что некоторые из особенностей поведения нашего естественного спутника обусловлены действием на Луну сил притяжения со стороны Солнца и Земли, которые и вызывают ее отклонение от движения по идеальной эллиптической орбите. В своих «Началах» Ньютон показал, что некоторые из неравномерностей в движениях Луны действительно объяснимы в рамках законов его механики и закона всемирного тяготения.

Ньютон также считал, что и кометы должны двигаться по эллиптическим орбитам, и побудил Эдмонда Галлея заняться теорией комет. Галлей собрал данные о кометах, которые наблюдались в прошлом. Он высказал предположение, что кометы, зарегистрированные в 1531, 1607 и 1682 гг., на самом деле одна и та же комета. Применив теорию Ньютона, Галлей предсказал, что следующее прохождение той же кометы произойдет в конце 1758 г. или в начале 1759 г. Комета (позднее названная именем Галлея) действительно появилась под Рождество 1758 г., а ближайшую к Солнцу точку своей орбиты прошла 13 марта 1759 г. Ее наблюдали также в 1910 г.{6} Период кометы Галлея варьируется из‑за возмущений, вносимых в ее движение притяжением планет.

Однако Ньютон не располагал доказательством того, что все наблюдаемые нерегулярности в движениях Луны и планет обусловлены действием сил тяготения, как не смог он объяснить и устойчивость Солнечной системы (казалось бы, совместное действие подобных факторов должно со временем разрушить ее). Преемники Ньютона уже в XVIII в. продолжили исследование нерегулярностей в движениях планет Солнечной системы.

Орбита, по которой планета обращается вокруг Солнца, как знал еще Ньютон, была бы эллипсом лишь в том случае, если бы не существовало других планет. Но в Солнечной системе их девять, и многие из них имеют свои естественные спутники, и все они не только обращаются вокруг Солнца, но и притягиваются друг к другу в соответствии с законом всемирного тяготения Ньютона. Следовательно, их орбиты не могут быть идеально эллиптическими. Чтобы определить точные орбиты планет, пришлось бы решить общую задачу многих тел, т.е. оценить движение любого числа тел, каждое из которых, согласно закону всемирного тяготения, притягивает все остальные. Однако задача многих тел и поныне не поддается решению. Тем не менее двум выдающимся математикам XVIII в. удалось существенно продвинуться по пути, указанному Ньютоном.

Родившийся в Италии француз Жозеф Луи Лагранж (1736‑1813) со свойственным молодости бесстрашием взялся за решение математической задачи о движении Луны под действием притяжения Солнца и Земли и добился успеха, когда ему было двадцать восемь лет. Лагранж установил, что изменения видимой части Луны обусловлены экваториальными выпучиваниями Земли и Луны. Кроме того, ему удалось показать, что силы притяжения, действующие на Землю со стороны Солнца и Луны, вызывают довольно значительные колебания в положении земной оси. Таким образом, выяснилось, что периодические изменения в направлении оси вращения Земли – замеченные наблюдателями еще в античные времена – являются следствием закона всемирного тяготения, установленным теперь математическим путем.

Еще один важный шаг Лагранж сделал в математическом анализе движения спутников Юпитера. Проведенные им вычисления показали, что наблюдаемые возмущения также обусловлены действием гравитации. Результаты своих исследований Лагранж изложил в «Аналитической механике» (1788) – труде, в котором были обобщены и формализованы достижения Ньютона в механике. Лагранж как‑то пошутил, что Ньютон счастливейший из смертных, ибо существует лишь одна Вселенная и Ньютон открыл ее математические законы. Однако самому Лагранжу выпала честь продемонстрировать миру совершенство теории Ньютона.

Следствия, выведенные Лагранжем из законов Ньютона, были в дальнейшем приумножены его современником и соотечественником Пьером Симоном Лапласом (1749‑1827), не уступавшим Лагранжу по силе математического дарования. Лаплас не оставлял без внимания ни одну математическую идею, которая могла бы способствовать познанию природы. Лаплас всю свою жизнь посвятил астрономии, и какой бы областью математики он ни занимался, свою конечную цель всегда видел в том, чтобы применить математические методы в астрономии. Известно, что в своих работах Лаплас нередко опускал трудные математические детали, ограничиваясь замечанием: «Нетрудно видеть, что…» Истинная подоплека этого состоит в том, что ему было просто некогда останавливаться на деталях математических доказательств – так он спешил перейти к приложениям. Лаплас внес фундаментальный вклад в развитие математики, но многие его достижения были не более чем «побочным продуктом» его титанической деятельности на поприще естествознания, и впоследствии их подхватили и развили другие, исследователи.

Одним из впечатляющих достижений Лапласа стало доказательство периодичности возмущений в эксцентриситетах эллиптических планетных орбит. Иначе говоря, Лаплас доказал, что величины этих возмущений колеблются в определенных пределах, а не возрастают неограниченно, нарушая регулярность небесных движений. Смысл результата, полученного Лапласом, приближенно можно истолковать как утверждение об устойчивости Вселенной. Лаплас доказал это в своем эпохальном пятитомном труде «Небесная механика», публикация которого продолжалась в течение двадцати шести лет (1799‑1825). В этом сочинении, увенчавшем труд всей его жизни, Лаплас подвел итог исследованиям, проведенным им и Лагранжем:

В первой части нашего сочинения мы изложили общие принципы равновесия и движения тел. Применение этих принципов к движениям небесных тел привело нас с помощью одних лишь математических рассуждений и без какой бы то ни было гипотезы к закону всемирного тяготения – действие силы тяжести и движение брошенных тел являются частными случаями этого закона. Мы рассмотрели систему тел, подверженных действию этого великого закона природы, и с помощью несколько необычного анализа получили общие выражения для их движений, фигур и колебаний покрывающей их жидкости. Из этих выражений мы вывели все известные явления: такие, как прилив и отлив, вариации степени и интенсивности силы тяжести по поверхности Земли, предварение равноденствий, либрация Луны, фигура и вращение колец Сатурна. Мы также указали причину, по которой эти кольца постоянно остаются в плоскости экватора Сатурна. Кроме того, из той же теории гравитации мы вывели основные уравнения движений планет, в том числе Юпитера и Сатурна, у которых нерегулярности [движения] имеют период свыше 900 лет.

Лаплас пришел к выводу, что природа создала небесную машину, «дабы, та действовала вечно, на тех же принципах, которые столь великолепно проявляются на Земле во имя сохранения отдельных особей и непрекращающегося существования видов».

Но ньютоновскую теорию гравитации ожидали еще более впечатляющие результаты. Однако замечательное следствие из общей астрономической теории Лагранжа и Лапласа заслуживает того, чтобы упомянуть о нем особо. Мы имеем в виду чисто теоретическое предсказание существования и местоположения тогда еще неизвестной планеты Нептун. Галилей наблюдал ее в 1613 г., но думал, что видит звезду. Была выдвинута гипотеза, что необъяснимые возмущения в движении планеты Уран, замеченные примерно в 1820 г., обусловлены гравитационным притяжением со стороны какой‑то неведомой планеты. Два астронома – двадцатишестилетний математик из Кембриджа Джон Кауч Адамс (1819‑1892) и директор Парижской обсерватории Урбен Жан Жозеф Леверье (1811‑1877) – независимо друг от друга вычислили орбиту гипотетической планеты, пользуясь данными наблюдений и основываясь на общей астрономической теории. В 1841 г. Адамс вычислил массу, орбиту и положение планеты, получившей впоследствии название Нептун. Он посетил директора Гринвичской королевской обсерватории Джорджа Эйри, чтобы сообщить о результатах своих вычислений. Застав Эйри за обедом, Адамс оставил ему рукопись, попросив ознакомиться с ней. После некоторых проволочек Эйри прочитал работу Адамса, но особого впечатления она на него не произвела. Между тем Леверье отправил свои результаты с указанием предполагаемого местоположения новой планеты немецкому астроному Иоганну Галле. Получив письмо от Леверье, Галле в тот же вечер (23 сентября 1846 г.) наблюдал Нептун. В телескопы того времени Нептун был едва различим, и вряд ли его удалось бы заметить, если бы астрономы не искали планету специально, руководствуясь теоретическим предсказанием.

Задача, решенная Адамсом и Леверье, была необычайно трудна. Им пришлось действовать как бы в обратном направлении: вместо того чтобы вычислять, какие возмущения вносит в движение других планет известная планета (с известной массой и орбитой), они оценили массу и определили орбиту неизвестной планеты по возмущениям, вносимым ею в движение Урана. Успех Адамса и Леверье был воспринят повсюду как триумф теории и окончательное доказательство универсального характера закона всемирного тяготения Ньютона.

Но все попытки понять физическую природу гравитации неизменно заканчивались неудачей. Этим вопросом задавался еще Галилей. В его «Диалоге о двух главнейших системах мира» два действующих лица – Сальвиати и Симпличио – ведут между собой такой разговор:

Сальвиати… И если он [автор] определит мне природу движителя одного из этих движущихся тел, то я обязуюсь доказать ему, что заставляет двигаться Землю. И более того, я сделаю то же самое, если он сумеет объяснить мне, что именно движет частицы Земли вниз.

Симпличио. Причина этого явления общеизвестна, и всякий знает, что эта тяжесть.

Сальвиати. Вы ошибаетесь, синьор Симпличио, вы должны были бы сказать – всякий знает, что это называется тяжестью, но я вас спрашиваю не о названии, а о сущности вещи; об этой сущности вы знаете ничуть не больше, чем о сущности того, что движет звезды по кругу, за исключением названия, которое было к нему приложено и стало привычным и ходячим благодаря опыту, повторяющемуся на наших глазах тысячу раз в день. Но это не значит, что мы в большей степени понимали и знали принцип или ту силу, которая движет книзу камень, сравнительно с теми, которые, как мы знаем, дают камню при отбрасывании движение вверх или движут Луну по кругу. Мы не знаем ничего, за исключением, как я сказал, названия, которое для данного специального случая известно как «тяжесть», тогда как для другого имеется более общий термин – «приложенная сила», или же «образующее разумение», и для бесконечного множества других движений выставляется причиной «природа».

([12], т. 1, с. 120.)

Ньютон также столкнулся с проблемой объяснения природы тяготения и вынужден был признать:

До сих пор я изъяснял небесные явления и приливы наших морей на основании силы тяготения, но я не указывал причины самого тяготения… Причину же этих свойств силы тяготения я до сих пор не мог вывести из явлений, гипотез же я не измышляю. Все же, что не выводится из явлений, должно называться гипотезою , гипотезам же метафизическим, физическим, механическим, скрытым свойствам не место в экспериментальной философии.