Анализ временной диаграммы
Анализ проведем на уже рассмотренном примере.
Сначала нужно дождаться установившегося режима. Откидываем первые четыре заявки как нехарактерные, протекающие во время процесса установления работы системы. Измеряем время наблюдения, допустим, что в нашем примере оно составит Tн = 5 часов. Подсчитываем из диаграммы количество обслуженных заявок Nобс., времена простоя и другие величины. В результате можем вычислить показатели, характеризующие качество работы СМО.
- Вероятность обслуживания: Pобс. = Nобс./N = 5/7 = 0.714. Для расчета вероятности обслуживания заявки в системе достаточно разделить число заявок, которым удалось обслужиться за время Tн (см. линейку «Обслуженные») Nобс., на число заявок N, которые хотели обслужиться за это же время. Как и раньше вероятность экспериментально определяем отношением свершившихся событий к общему числу событий, которые могли совершиться!
- Пропускная способность системы: A = Nобс./Tн = 7/5 = 1.4 [шт/час]. Для расчета пропускной способности системы достаточно разделить число обслуженных заявок Nобс. на время Tн, за которое произошло это обслуживание (см. линейку «Обслуженные»).
- Вероятность отказа: Pотк. = Nотк./N = 3/7 = 0.43. Для расчета вероятности отказа заявке в обслуживании достаточно разделить число заявок Nотк., которым отказали за время Tн (см. линейку «Отказанные»), на число заявок N, которые хотели обслужиться за это же время, то есть поступили в систему. Обратите внимание. Pотк. + Pобс. в теории должно быть равно 1. На самом деле экспериментально получилось, что Pотк. + Pобс. = 0.714 + 0.43 = 1.144. Эта неточность объясняется тем, что время наблюдения Tн мало и статистика накоплена недостаточная для получения точного ответа. Погрешность это показателя сейчас составляет 14%!
- Вероятность занятости одного канала: P1 = Tзан./Tн = 0.05/5 = 0.01, где Tзан. — время занятости только одного канала (первого или второго). Измерениям подлежат временные отрезки, на которых происходят определенные события. Например, на диаграмме ищутся такие отрезки, во время которых заняты или первый или второй канал. В данном примере есть один такой отрезок в конце диаграммы длиной 0.05 часа. Доля этого отрезка в общем времени рассмотрения (Tн = 5 часов) определяется делением и составляет искомую вероятность занятости.
- Вероятность занятости двух каналов: P2 = Tзан./Tн = 4.95/5 = 0.99. На диаграмме ищутся такие отрезки, во время которых одновременно заняты и первый, и второй канал. В данном примере таких отрезков четыре, их сумма равна 4.95 часа. Доля продолжительности этих события в общем времени рассмотрения (Tн = 5 часов) определяется делением и составляет искомую вероятность занятости.
- Среднее количество занятых каналов: Nск = 0 · P0 + 1 · P1 + 2 · P2 = 0.01 + 2 · 0.99 = 1.99. Чтобы подсчитать, сколько каналов занято в системе в среднем, достаточно знать долю (вероятность занятости одного канала) и умножить на вес этой доли (один канал), знать долю (вероятность занятости двух каналов) и умножить на вес этой доли (два канала) и так далее. Полученная цифра 1.99 говорит о том, что из возможных двух каналов в среднем загружено 1.99 канала. Это высокий показатель загрузки, 99.5%, система хорошо использует ресурс.
- Вероятность простоя хотя бы одного канала: P*1 = Tпростоя1/Tн = 0.05/5 = 0.01.
- Вероятность простоя двух каналов одновременно: P*2 = Tпростоя2/Tн = 0.
- Вероятность простоя всей системы: P*c = Tпростоя сист./Tн = 0.
- Среднее количество заявок в очереди: Nсз = 0 · P0з + 1 · P1з + 2 · P2з = 0.34 + 2 · 0.64 = 1.62 [шт]. Чтобы определить среднее количество заявок в очереди, надо определить отдельно вероятность того, что в очереди будет одна заявка P1з, вероятность того, в очереди будет стоять две заявки P2з и т. д. и снова с соответствующими весами их сложить.
- Вероятность того, что в очереди будет одна заявка: P1з = T1з/Tн = 1.7/5 = 0.34 (всего на диаграмме четырех таких отрезка, в сумме дающих 1.7 часа).
- Вероятность того, в очереди будет стоять одновременно две заявки: P2з = T2з/Tн = 3.2/5 = 0.64 (всего на диаграмме три таких отрезка, в сумме дающих 3.25 часа).
- Среднее время ожидания заявки в очереди:
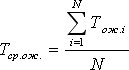
(Сложить все временные интервалы, в течение которых какая-либо заявка находилась в очереди, и разделить на количество заявок). На временной диаграмме таких заявок 4.
- Среднее время обслуживания заявки:
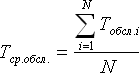
(Сложить все временные интервалы, в течение которых какая-либо заявка находилась на обслуживании в каком-либо канале, и разделить на количество заявок).
- Среднее время нахождения заявки в системе: Tср. сист. = Tср. ож. + Tср. обсл..
- Среднее количество заявок в системе:
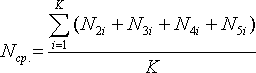
Разобьем интервал наблюдения, например, на десятиминутки. Получится на пяти часах K подынтервалов (в нашем случае K = 30). В каждом подынтервале определим по временной диаграмме, сколько заявок в этот момент находится в системе. Смотреть надо на 2, 3, 4 и 5-ю линейки — какие из них заняты в данный момент. Затем сумму K слагаемых усреднить.
Далее следует оценить точность каждого из полученных результатов. То есть ответить на вопрос: насколько мы можем доверять этим значениям?
Если точность не является удовлетворительной, то следует увеличить время эксперимента и тем самым улучшить статистику. Можно сделать и по-другому. Снова несколько раз запустить эксперимент на время Tн. А в последствии усреднить значения этих экспериментов. И снова проверить результаты на критерий точности. Эту процедуру следует повторять до тех пор, пока не будет достигнута требуемая точность.
Далее следует составить таблицу результатов и оценить значения каждого из них с точки зрения клиента и владельца СМО (см. табл. 30.3).. В конце, учитывая сказанное в каждом пункте, следует сделать общий вывод. Таблица должна иметь примерно такой вид, какой показан в табл. 10.3.
| Таблица 10.3. Показатели СМО | |||||||||||||||||||||||
|
Синтез СМО
Мы проделали анализ существующей системы. Это дало возможность увидеть ее недостатки и определить направления улучшения ее качества. Но остаются непонятными ответы на конкретные вопросы, что именно надо сделать — увеличивать количество каналов или увеличивать их пропускную способность, или увеличивать количество мест в очереди, и, если увеличивать, то насколько? Есть и такие вопросы, что лучше — создать 3 канала с производительностью 5 шт/час или один с производительностью 15 шт/час?
Чтобы оценить чувствительность каждого показателя к изменению значения определенного параметра, поступают следующим образом. Фиксируют все параметры кроме одного, выбранного. Затем снимают значение всех показателей при нескольких значениях этого выбранного параметра. Конечно, приходится повторять снова и снова процедуру имитации и усреднять показатели при каждом значении параметра, оценивать точность. Но в результате получаются надежные статистические зависимости характеристик (показателей) от параметра.
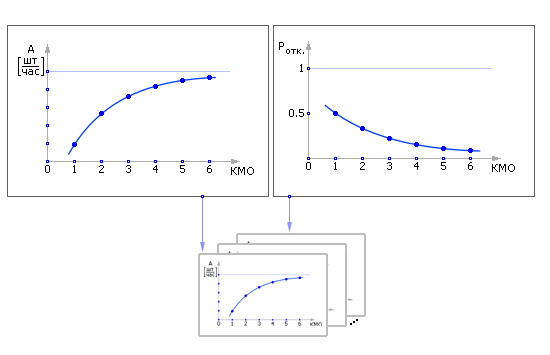
Например, для 12 показателей нашего примера можно получить 12 зависимостей от одного параметра: зависимость вероятности отказов Pотк. от количества мест в очереди (КМО), зависимость пропускной способности A от количества мест в очереди, и так далее (см. рис. 10.8).
| |
| Рис. 10.8. Примерный вид зависимостей показателей от параметров СМО |
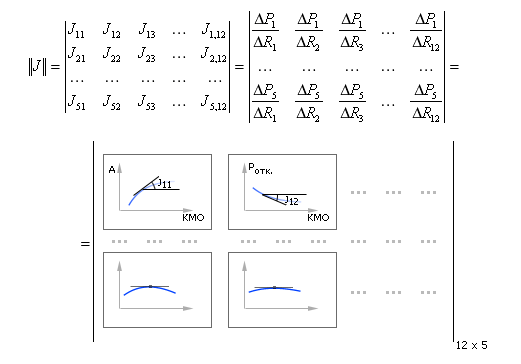
Затем так же можно снять еще 12 зависимостей показателей P от другого параметра R, зафиксировав остальные параметры. И так далее. Образуется своеобразная матрица зависимостей показателей P от параметров R, по которой можно провести дополнительный анализ о перспективах движения (улучшения показателей) в ту или иную сторону. Наклон кривых хорошо показывает чувствительность, эффект от движения по определенному показателю. В математике эту матрицу называют якобианом J, в которой роль наклона кривых играют значения производных ΔPi/ΔRj, см. рис. 10.9. (Напомним, что производная связана геометрически с углом наклона касательной к зависимости.)
| |
| Рис. 10.9. Якобиан — матрица чувствительностей показателей в зависимости от изменения параметров СМО |
Если показателей 12, а параметров, например, 5, то матрица имеет размерность 12 x 5. Каждый элемент матрицы — кривая, зависимость i-го показателя от j-го параметра. Каждая точка кривой — среднее значение показателя на достаточно представительном отрезке Tн или усреднено по нескольким экспериментам.
Следует понимать, что кривые снимались в предположении того, что все параметры кроме одного в процессе их снятия были неизменны. (Если бы все параметры меняли значения, то кривые были бы другими. Но так не делают, так как получится полная неразбериха и зависимостей не будет видно.)
Поэтому, если на основании рассмотрения снятых кривых принимается решение о том, что некоторый параметр будет в СМО изменен, то все кривые для новой точки, в которой опять будет исследоваться вопрос о том, какой параметр следует изменить, чтобы улучшить показатели, следует снимать заново.
Так шаг за шагом можно попытаться улучшить качество системы. Но пока эта методика не может ответить на ряд вопросов. Дело в том, что, во-первых, если кривые монотонно растут, то возникает вопрос, где же все-таки следует остановиться. Во-вторых, могут возникать противоречия, один показатель может улучшаться при изменении выбранного параметра, в то время как другой будет одновременно ухудшаться. В-третьих, ряд параметров сложно выразить численно, например, изменение дисциплины обслуживания, изменение направлений потоков, изменение топологии СМО. Поиск решения в двух последних случаях проводится с применением методов экспертизы и методами искусственного интеллекта.
Поэтому сейчас обсудим только первый вопрос. Как принять решение, каким должно быть все-таки значение параметра, если с его ростом показатель все время монотонно улучшается? Вряд ли значение бесконечности устроит инженера.
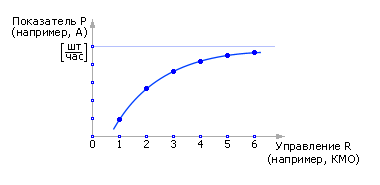
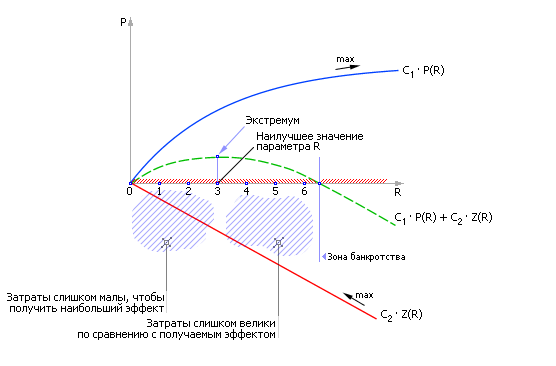
Параметр R — управление, это то, что находится в распоряжении владельца СМО (например, возможность заасфальтировать площадку и тем самым увеличить количество мест в очереди, поставить дополнительные каналы, увеличить поток заявок за счет увеличения затрат на рекламу и так далее). Меняя управление, можно влиять на значение показателя P, цель, критерий (вероятность отказов, пропускную способность, среднее время обслуживания и так далее). Из рис. 10.10 видно, что если увеличивать управление R, то можно добиться всегда улучшение показателя P. Но очевидно, что любое управление связано с затратами Z. И чем больше прилагают усилия для управления, чем больше значение управляющего параметра, тем больше затраты. Обычно затраты на управление растут линейно: Z = C1 · R. Хотя встречаются случаи, когда, например, в иерархических системах, они растут экспоненциально, иногда — обратно экспоненциально (скидки за опт) и так далее.
| |
| Рис. 10.10. Зависимость показателя Р от управляемого параметра R (пример) |
В любом случае ясно, что когда-то вложение все новых затрат просто перестанет себя окупать. Например, эффект от заасфальтированной площадки размером в 1 км2 вряд ли окупит затраты владельца бензоколонки в Урюпинске, там просто не будет столько желающих заправиться бензином. Иными словами показатель P в сложных системах не может расти бесконечно. Рано или поздно его рост замедляется. А затраты Z растут (см. рис. 10.11).
| |
| Рис. 10.11. Зависимости эффекта от применения показателя Р и затрат Z на его получение как функции управляемого параметра R |
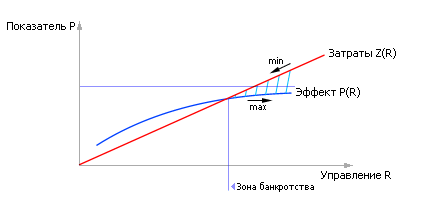
Из рис. 10.11 видно, что при назначении цены C1 за единицу затрат R и цены C2 за единицу показателя P, эти кривые можно сложить. Кривые складывают, если их требуется одновременно минимизировать или максимизировать. Если одна кривая подлежит максимизации, а другая минимизации, то следует найти их разность, например по точкам. Тогда результирующая кривая (см. рис. 10.12), учитывающая и эффект от управления и затраты на это, будет иметь экстремум. Значение параметра R, доставляющего экстремум функции, и есть решение задачи синтеза.
| |
| Рис. 10.12. Суммарная зависимость эффекта от применения показателя Р и затрат Z на его получение как функции управляемого параметра R |
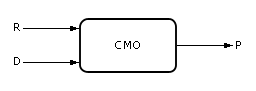
Кроме управления R и показателя P в системах действует возмущение. Возмущения обозначим как D = {d1, d2, …}, см. рис. 10.13. Возмущение — это входное воздействие, которое, в отличие от управляющего параметра, не зависит от воли владельца системы. Например, низкие температуры на улице, конкуренция снижают, к сожалению, поток клиентов, поломки оборудования досадно снижают производительность системы. И управлять этими величинами непосредственно владелец системы не может. Обычно возмущение действует «назло» владельцу, снижая эффект P от управляющих усилий R. Это происходит потому, что, в общем случае, система создается для достижения целей, недостижимых самих по себе в природе. Человек, организуя систему, всегда надеется посредством ее достичь некоторой цели P. На это он затрачивает усилия R, идя наперекор природе. Система — организация доступных человеку, изученных им природных компонент для достижения некоторой новой цели, недостижимой ранее другими способами.
| |
| Рис. 10.13. Условное обозначение изучаемой системы, на которую воздействуют управляющие воздействия R и возмущения D |
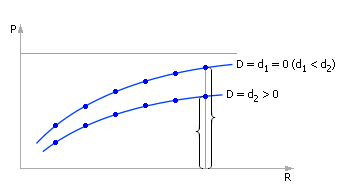
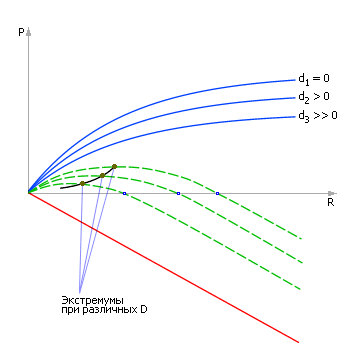
Итак, если мы снимем зависимость показателя P от управления R еще раз (как показано на рис. 10.10), но в условиях появившегося возмущения D, то, возможно, характер кривой изменится. Скорее всего, показатель будет при одинаковых значениях управлений находиться ниже, так как возмущение носит «противный» характер, снижая показатели системы (см. рис. 10.14). Система, предоставленная сама себе, без усилий управляющего характера, перестает обеспечивать цель, для достижения которой она была создана. Если, как и ранее, построить зависимость затрат, соотнести ее с зависимостью показателя от параметра управления, то найденная точка экстремума сместится (см. рис. 10.15) по сравнению со случаем «возмущение = 0» (см. рис. 10.12).
| |
| Рис. 10.14. Зависимость показателя P от управляющего параметра R при различных значениях действующих на систему возмущений D |
Если снова увеличить возмущение, то кривые изменятся (см. рис. 10.14) и, как следствие, снова изменится положение точки экстремума (см. рис. 10.15).
| |
| Рис. 10.15. Нахождение точки экстремума на суммарной зависимости при различных значениях действующего возмущающего фактора D |
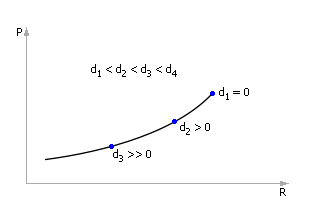
В конечном итоге, все найденные положения точек экстремума переносятся на новый график, где образуют зависимость Показателя P от Управляющего параметра R при изменении Возмущений D (см. рис. 10.16).
| |
| Рис. 10.16. Зависимость показателя P от управляющего параметра R при изменении значений возмущений D (кривая состоит только из точек экстремумов) |
Обратите внимание, что на самом деле на этом графике могут быть и другие рабочие точки (график пронизан как бы семействами кривых), но нанесенные нами точки задают такие координаты управляющего параметра, при которых при заданных возмущениях (!) достигается наибольшее из возможных значение показателя P.
Этот график (см. рис. 10.16) связывает Показатель P, Управление (ресурс) R и Возмущение D в сложных системах, указывая, как действовать наилучшим образом ЛПР (лицу, принимающему решение) в условиях возникших возмущений. Теперь пользователь может, зная реальную обстановку на объекте (значение возмущения), быстро по графику определить, какое управляющее воздействие на объект необходимо, чтобы обеспечить наилучшее значение интересующего его показателя.
Заметьте, если управляющее воздействие будет меньше оптимального, то суммарный эффект снизится, возникнет ситуация недополученной прибыли. Если управляющее воздействие будет больше оптимального, то эффект также снизится, так как заплатить за очередное увеличение управляющих усилий надо будет по величине больше, чем та, которую вы получите в результате ее использования (ситуация банкротства).
Примечание. В тексте лекции мы использовали слова «управление» и «ресурс», то есть считали, что R = U. Следует пояснить, что управление действительно играет роль некоторой ограниченной ценности для владельца системы. То есть всегда является ценным для него ресурсом, за который всегда приходится платить, и которого всегда не хватает. Действительно, если бы эта величина не была ограничена, то мы бы могли достигать за счет бесконечной величины управлений бесконечно больших значений целей, а вот бесконечно больших результатов в природе явно не наблюдается.
Иногда различают собственно управление U и ресурс R, называя ресурсом некоторый запас, то есть границу возможного значения управляющего воздействия. В этом случае понятия ресурс и управление не совпадают: U < R. Иногда различают предельное значение управления U ≤ R и интегральный ресурс ∫Udt ≤ R.