Функция распределения случайной величины и ее свойства. Функция распределения дискретной случайной величины
Одним из наиболее удобных и универсальных способов задания закона распределения случайной величины X является функция распределения.
Функцией распределения (или интегральной функцией распределения) случайной величины X называется функция 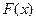 , которая для любого числа
, которая для любого числа 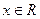 равна вероятности события, состоящего в том, что случайная величина
равна вероятности события, состоящего в том, что случайная величина 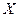 примет значение, меньшее, чем
примет значение, меньшее, чем 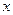 , т. е.
, т. е. 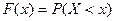 .
.
Геометрически функция распределения интерпретируется как вероятность того, что случайная точкаX попадет левее данной точки x (рис. 2).

Рис. 2
Функция F(x) существует как для дискретных, так и непрерывных случайных величин.
Функция распределения обладает следующими свойствами:
1. 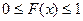 ;
;
2. 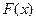 - неубывающая функция, т. е.
- неубывающая функция, т. е. 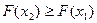 , если
, если 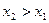 ;
;
3. 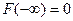 ,
, 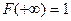 ;
;
4. 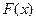 - непрерывна слева в любой точке x, т. е.
- непрерывна слева в любой точке x, т. е. 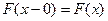 ,
, 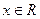 ;
;
5. 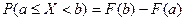 .
.
Функция распределения дискретной случайной величины имеет вид:
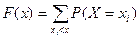 ,
,
где суммирование ведется по всем индексам 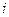 , для которых
, для которых 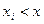 . Для дискретной случайной величиныфункция распределения естьразрывная ступенчатая функция, непрерывная слева.
. Для дискретной случайной величиныфункция распределения естьразрывная ступенчатая функция, непрерывная слева.
Функция распределения и плотность вероятности непрерывной случайной величины
С помощью функции распределения можно дать более строгое определение непрерывной случайной величины.
Случайная величина X называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.
В отличие от дискретных случайных величин вероятность отдельного значения для непрерывной случайной величины равна нулю: 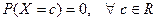 . Поэтому для непрерывной случайной величины X имеем
. Поэтому для непрерывной случайной величины X имеем
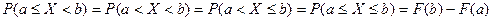 . (*)
. (*)
Для непрерывных случайных величин кроме функции распределения существует еще один удобный способ задания закона распределения – плотность вероятности.
Пусть функция распределения 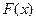 данной непрерывной случайной величины X непрерывна и дифференцируема всюду, кроме, может быть, отдельных точек.
данной непрерывной случайной величины X непрерывна и дифференцируема всюду, кроме, может быть, отдельных точек.
Плотностью распределения непрерывной случайной величины X (или плотностью вероятности, или просто плотностью) называется функция 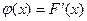 .
.
Функцию 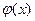 называют также дифференциальной функцией распределения.
называют также дифференциальной функцией распределения.
Плотность распределения любой непрерывной случайной величины неотрицательна, т. е. 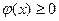 ; обладает свойством нормированности:
; обладает свойством нормированности:
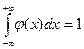 ;
; 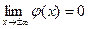 .
.
График функции 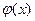 называется кривой распределения.
называется кривой распределения.
Функция распределения F(x) выражается через плотность распределения формулой
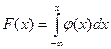 (1)
(1)
Вероятность попадания непрерывной случайной величины 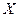 в промежуток
в промежуток 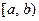 определяется равенством:
определяется равенством:
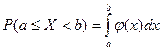 . (2)
. (2)
Числовые характеристики случайных величин
