Доказательство (принадлежит Маркову)

II

II

II

Рассмотрим кодирование слова минимальной длины, которое допускает, по крайней мере, две различных расшифровки, т.е. для которого найдется, по крайней мере, два различных исходных слова, кодирующим для которых является данное слово. Рассмотрим две различных его расшифровки. Кодовые слова первой расшифровки обведены сверху, а кодовые слова второй расшифровки – снизу. Разрежем кодирующее слово по границам кодовых слов. В результате получим слова-отрезки. Эти слова разобьем на две группы:
1-ая 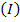– слова, которые являются кодовыми;
2-ая 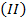– слова, которые не являются кодовыми, т.е. все остальные.

Слова 2-ой группы являются либо началом кодовых слов второй расшифровки и концом кодовых слов первой расшифровки, либо началом кодовых слов первой расшифровки и концом кодовых слов второй расшифровки.

Слова 2-ой группы попарно различны. Если бы это было не так, т.е. существовали два одинаковых слова 2-ой группы, то вырежем участок между двумя одинаковыми словами 2-ой группы вместе с одним из этих слов и соединим полученные два слова. Тогда не трудно видеть, что полученное слово также допускает две дешифровки, что противоречит минимальности некорректного данного слова.

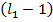Посчитаем, какое максимальное число слов во 2-ой группе может быть. Во 2-ой группе есть непустые начала кодовых слов, которые отличны от самих кодовых слов. Первое слово имеет длину и поэтому число рассмотренных начал для него есть , для второго кодового слова число начал равно 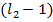, и так для каждого, а для последнего – . Суммируя данные величины, получаем, что число слов во 2-ой группе не более чем .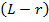

Слова второй группы разбивают исходное слово на не более чем 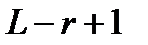кусков.

Теперь разобьем слова 2-ой группы на пары соседних и рассмотрим последовательность слова 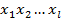. Таких пар слов не больше, чем 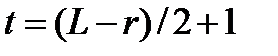(в случае нечетного числа слов, последнее непарное слово – дополнительное). Число кодовых слов в каждом из полученных 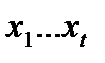не более 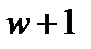по обеим кодировкам. Согласно одному разбиению в одной половине уложатся не более одного кодового слова, а в другой – не более 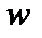(согласно второму разбиению ситуация симметрична).

Поэтому общее число кодовых слов, которое содержится в начальном слове не более чем 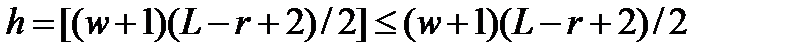. Что и требовалось показать.

Критерий префиксного кодирования Мак-Миллана.

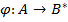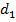Определение. Кодирование называют типа , если существует штук кодовых слов единичной длины, кодовых слов из двух букв, 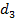слов из трех букв, …, 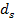слов длины .

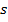Критерий. Префиксное корректное кодирование типа существует тогда и только тогда, когда

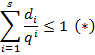
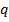– мощность кодирующего алфавита.

Доказательство.

Необходимость. Пусть 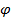– корректное кодирование типа . Покажем справедливость формулы .

Перепишем формулу в виде:

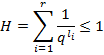
– длины кодовых слов. Возведем сумму в степень :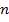
,
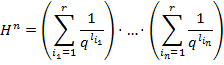т.е. возьмем 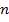произведений таких сумм

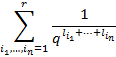
здесь параметры 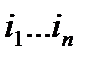независимо друг от друга пробегают множество от 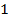до :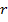
,
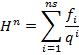где 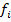– число представлений числа 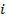в виде суммы 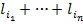с помощью группировки слагаемых. Т.к. кодирование корректно, то .

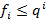Действительно, – это общее число слов в кодирующем алфавите длины , а каждое решение уравнения 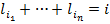будет соответствовать некоторому кодирующему слову, которых, в силу корректности, не может быть больше чем общее число слов длины :

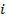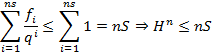
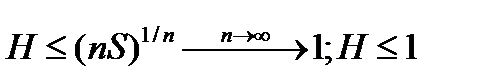
Достаточность. Пусть числа удовлетворяют соотношению 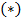. Построим префиксное кодирование типа .

Перепишем сумму 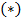по слагаемым:

Наша задача – построение кодовых слов таких, что никакое кодовое слово не начинается на другое кодовое слово. Построим в начале кодовые слова единичной длины, а потом длины 2 и т.д.

Из неравенства 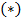следует, что 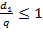, т.е. 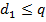. В кодирующем алфавите есть 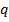букв и мы должны выбрать 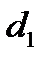различных кодовых слов единичной длины, а из неравенства 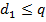следует, что это действительно можно сделать.

Далее построим кодовые слова длины 2. Тогда выполняется неравенство 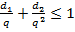, из которого следует, что 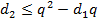, где – общее число слов длины 2 в кодовом алфавите, а 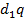– число слов длины 2, которые начинаются на кодовые слова единичной длины. Таким образом, число допустимых слов длины 2 равно 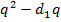. Из полученного неравенства следует, что мы действительно можем выбрать кодовые слова длины 2, чтобы выполнялись условия префиксности.

Допустим, что уже выбраны кодовые слова длины меньшей 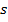, причем соблюдая условия префиксности. Покажем, что можно выбрать кодовые слова длины .

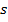Из неравенства следует, что
,
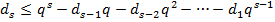где 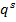– общее число слов длины 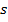в кодирующем алфавите, – число слов длины 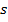, которые начинаются на кодовые слова длины 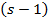и т. д., 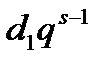число слов длины 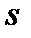, которые начинаются на кодовые слова длины 1. Таким образом, мы построили префиксное кодирование типа .

Теория кодирования имеет применение в задачах устойчивой пердачи информации.

Практические задачи

Контрольная работа 1: