Исследование затухающих и вынужденных

КОЛЕБАНИЙ

Цель работы:изучение затухающих колебаний физического маятника и вынужденных колебаний математического маятника.

Упражнение 1

Определение периода колебаний, коэффициента затухания, логарифмического декремента затухания и приведенной длины

физического маятника

I. Описание установки.

Прибор представляет собой комбинацию маятников: физического маятника «M» и связанного с ним маятника «m», который можно считать «математическим».

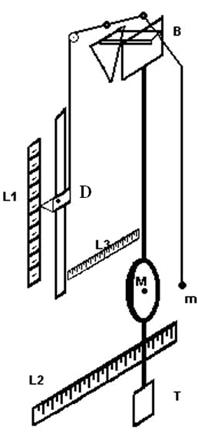
Рис. 4.1. Схема установки с физическим и математическим маятниками

Длина математического маятника считается от вилки «B» (рис. 4.1) до середины шарика «m». Она изменяется путем перемещения нити и фиксируется на масштабной линейке L₁ ползунком «D».

Амплитуды колебаний физического и математического маятников определяются соответственно по шкалам L₂ и L₃ (амплитуды измеряются в угловых единицах).

II. Методика работы

Физическим маятником называют тело, которое может свободно вращаться вокруг оси О, не проходящей через центр тяжести тела С (рис.4.2).

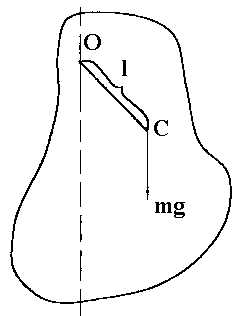
Рис.4.2

В положении равновесия центр тяжести расположен по вертикали под осью. Если мы теперь отклоним маятник на угол α, то возникает вращающий момент силы тяжести

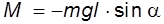(4.1)

где m – масса маятника , кг

g = 9,81 м/с² – ускорение силы тяжести;

l – расстояние от центра тяжести С до О, м.

Маятник начнет двигаться под действием этого момента.

Если затухания нет (b = 0), то выражение для периода незатухающих колебаний

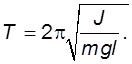(4.2)

Частным случаем физического маятника является математический маятник – материальная точка, подвешенная на нерастяжимой невесомой нити. В этом случае момент инерции 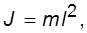и период определяется по формуле

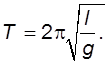(4.3)

Для описания колебаний физического маятника часто пользуются понятием приведенной длины 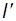маятника. Приведенной длиной физического маятника называется длина математического маятника, имеющего такой же период колебаний. Из формул (4.2) и (4.3) следует

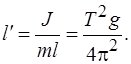(4.4)

При движении на маятник будет действовать тормозящий момент сил сопротивления воздуха и трения в опорах. Опыт показывает, что тормозящий момент сил можно приближенно считать пропорциональным угловой скорости w маятника

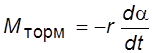, (4.5)

где r – коэффициент сопротивления.

Основное уравнение динамики для маятника имеет вид

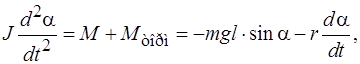(4.6)

где J – момент инерции.

При малых колебаниях (a <<1), sin α @ α и уравнение (4.6) принимает вид:

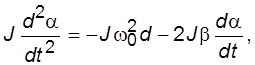(4.7)

где

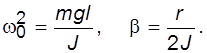(4.8)

Зависимость угла α от времени будет такой же, как в уравнении (II.6), то есть маятник будет совершать затухающие колебания, период которых определяется формулой (II.9).

Если прологарифмировать отношение измеренных начальной и конечной амплитуд, то с учетом (II.7) получим:

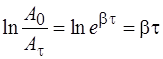, (4.9)

тогда

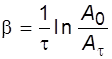, (4.10)

где τ – время измерения, за которое амплитуда уменьшилась до А_t .