Модификации алгоритма с возвратом для решения задач на максимум

ЗАДАЧА О РЮКЗАКЕ

УСЛОВИЕ. Заданы конечное множество A, положительные целые веса w(a), стоимости s(a) для каждого a Є A и общее ограничение на вес K.

ВОПРОС. Найти из всевозможных выборок A' A такую, чтобы суммарный вес входящих в него элементов не превосходил K, а суммарная стоимость была максимальна.

Задача о рюкзаке – задача об определении оптимальной выборки из N объектов, подчиненной некоторому ограничению. Поскольку из N объектов возможно сделать 2^N различных выборок, для решения подобной задачи с помощью алгоритма с возвратом необходимо очень сильное ограничение.

Вопрос 1. Изменим стоимости предметов на противоположные. Выборка максимальной стоимости превратилась в выборку минимальной стоимости. Почему нельзя эту задачу решить алгоритмом для решения задач на минимум, изложенным в предыдущем разделе?

Однако есть способ значительно сократить количество переборов – в процессе получения возможных решений помнить лучшее из полученных на данный момент решений и не пытаться генерировать те решения, которые будут заведомо хуже известного на данный момент оптимального решения.

ПРИНЦИП ВКЛЮЧЕНИЯ–НЕВКЛЮ­ЧЕНИЯ.

Каждый i-й объект проверяется на допустимость (согласно нашему ограничению). Затем внутри одной процедуры допустимый объект вначале включается в выборку, и с этим включенным объектом рекурсивно генерируются всевозможные решения и лучшее из них запоминается как оптимальное.

После этого происходит возврат и i-й объект удаляется из выборки.

Классический алгоритм с возвратом стал бы рекурсивно генерировать всевозможные решения без i-го объекта – принцип включения–невключения действует иначе.

Прежде, чем пытаться получать решения без i-го объекта, проверим, можно ли, не включив этот объект, получить решение лучшее, чем найденное оптимальное с i-м объектом. Если нет – то не стоит и пытаться.

Как проверить возможность получения без i-го объекта более ценной выборки, чем текущая оптимальная, если мы не собираемся сразу строить эти выборки?

Нужно посчитать стоимость, которую мы, может быть, наберем без i-го объекта. Для этого просуммируем стоимости всех предметов, уже вошедших в выборку, и стоимости всех еще неисследованных предметов(разумеется, без i-го объекта).

Если эта стоимость, которую, может быть, удастся набрать (а, может, и не удастся – ведь неисследованные объекты могут не пройти ограничение по весу!) будет больше оптимальной – есть смысл генерировать решения без i-го объекта.

Опишем рекурсивную процедуру TRY с включением-невклю­чением.

1 procedure try(i);

{i – номер объекта}

2 begin

3 IF ВКЛЮЧЕНИЕ ПРИЕМЛИМО THEN

4 begin

5 включить i-тый объект;

6 if i=N then проверить оптимальность

7 else try(i+1); {продолжить выборку}

8 удалить i-тый объект; {возврат}

9 end;

{оптимум с i-тым объектом запомнен, а сам объект
удален}

10 IF НЕВКЛЮЧЕНИЕ ПРИЕМЛИМО THEN

{подсчет возможной стоимости без i-того объекта и сравнение ее с оптимальной}

11 if i=N then проверить оптимальность

12 else try(i+1);

{строим выборки без i-того объекта}

13 end;

Пусть имеется 3 предмета и ограничение по весу 16:

НОМЕР
ВЕС
СТОИМОСТЬ

Первый раз из основной программы вызывается try(1). Рассмотрим трассировку алгоритма:

try(i)	№ 1	№ 2	№ 3	Сумма-рный вес	Суммарная стоимость	Возможная стоимость	Оптимальная стоимость	Примечания
try(1)	+	?	?					Вкл. 1
try(2)	+	+	?					Вкл. 2
try(3)	+	+	–					Оптимум
try(2)	+	–	?					25>18 Невкл. 2
try(3)	+	–	+					Оптимум
try(1)	–	?	?					23<25 Невкл. 1 неприем.

Последний оптимум, равный 25 достигается на выборке [1,3] и далее уже не меняется.

Прежде, чем записать алгоритм решения задачи о рюкзаке, сделаем полное описание глобальных переменных.

CONST N = 3;

VES = 16;

TYPE index = 1..N;

obj = record

v,st: integer {вес и стоимость}

end;

VAR A: array[index]of obj; {массив объектов}

X,OptX: array[index]of boolean;

{выборка, оптимальная выборка}

SumCost: integer;{общая стоимость всех объектов}

OptCost: integer; {оптимальная стоимость}

АЛГОРИТМ {Рюкзак}

Данные: Массив A записей obj, ограничение по весу VES.

Результаты: Выборка max ценности с ограничением по весу.

{Считаем, что массив записей A уже сформирован}

1 procedure My_try(i:index; sum_v,pos_st: integer);

{i – текущий объект, sum_v – вес текущей выборки,

pos_st – возможная стоимость}

2 begin

{включение}

3 if sum_v + A[i].v <= VES then

4 begin {проверка допустимости}

5 X[i]:= ложь;{включаем i-й}

6 if (i=N) and (pos_st > OptCost) then

7 begin {новый оптимум}

8 OptX:= X; OptCost:= pos_st

9 end

10 else

11 My_try(i+1, sum_v+A[i].v, pos_st);

{строим решения с i-тым объектом, pos_st не изменилась, т.к. i-тый объект из неисследованных перешел во включенные}

12 X[i]:= истина;{возврат}

13 end; {проверка допустимости}

{невключение}

14 st1:= pos_st–A[i].st; {возможная ценность
без i-того объекта}

15 if st1 > OptCost then

16 if i=N then

17 begin {новый оптимум}

18 OptX:= X; OptCost:= st1

19 end

20 else

{строим решения без i-того объекта}

21 My_try(i+1, sum_v, st1);

22 end;

1 begin {основная часть}

2 SumCost:= 0;

3 for i:=1 to N do

4 begin

5 SumCost:= SumCost+A[i].st;

6 X[i]:= истина; OptX[i]:= истина;

7 end;

8 OptCost:=0;

9 My_try(1, 0, SumCost);

10 печать OptX, OptCost;

11 end.

Вопрос 2. Почему первый вызов My_Try происходит с возможной стоимостью, равной SumCost?

Вопрос 3. Почему мы передаем суммарный вес рюкзака и возможную стоимость в виде параметров, а не вычисляем их внутри процедуры My_Try в цикле за O(N) шагов?

Ответ 1. При удлинении решения будет добавляться отрицательная стоимость, в результате чего будет происходить уменьшение целевой функции cost, в то время как она не должна убывать.

Ответ 2. Все предметы неисследованы.

Ответ 3. В наихудщем случае обращение к My_Try будет происходить 2^N раз и, соответственно, этот цикл будет выполняться 2^N раз.

Кратчайшие пути

В этом разделе будут рассмотрены алгоритмы поиска маршрутов, позволяющие не только «дойти до выбранного места», но и сделать это «самым коротким путем».

Дадим основные определения и обозначения для объектов, из которых будет построена наша математическая модель.

Будем рассматривать ориентированные графы, дугам которых приписаны веса (рис. 10.1).

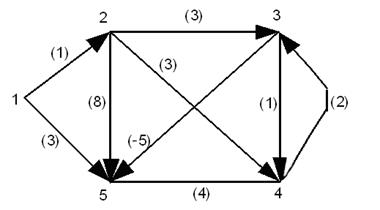
Рис. 10.1. Модельный граф

Это означает, что каждой дуге (u→v) поставлено в соответствие вещественное число A[u,v]. Матрицу весов дуг данного графа будем обозначать A, несуществующим дугам будем приписывать веса, равные +¥, т.е. A[u,v] = +¥, если дуга (u→v) не существует.

Матрица весов A для модельного графа (рис. 10.1):

+¥		+¥	+¥
+¥	+¥
+¥	+¥	+¥		-5
+¥	+¥		+¥	+¥
+¥	+¥	+¥		+¥

В программе граф будет задаваться матрицей весов и (если потребуется) списками инцидентности PRED и SLED. В списках PRED для каждой вершины v хранится список ее предшественниц u, т.е. вершин, из которых дуга идет в эту вершину.

В списках SLED для каждой вершины v хранится список ее потомков, т.е. вершин, в которые из v идет дуга.

Длина пути будет подсчитываться как сумма весов, входящих в него дуг.

Зафиксируем в графе пару вершин s (источник) и t (сток).

Длину кратчайшего пути от s до t будем обозначать D[s, t], где D – матрица расстояний между всеми парами вершин. Если такого пути не существует, то будем считать, что D[s, t] = +¥.

Если источник s зафиксирован, то расстояния от s до остальных вершин графа будут храниться в векторе (одномерном массиве) D, где D[v] – расстояние от s до v.

Как видно из определения, дугам могут быть приписаны отрицательные веса. Если в графе существует контур (замкнутый путь) отрицательной длины, то понятие кратчайшего пути теряет смысл: обходя этот контур сколь угодно большое число раз, можно сделать длину пути как угодно малой.

Если потребовать, чтобы в качестве кратчайшего пути искать только элементарные пути, т.е. пути, не содержащие контуров, то задача станет вполне корректной, но, увы, NP – полной. Поскольку мы собираемся решать нашу задачу не алгоритмом с возвратом, а разработать для нее эффективные полиномиальные алгоритмы, придется умерить свои требования и поставить задачу так, чтобы мы могли ее решить.

Окончательная постановка: БУДЕМ ИСКАТЬ КРАТЧАЙШИЕ ПУТИ НА ГРАФАХ БЕЗ КОНТУРОВ ОТРИЦАТЕЛЬНОЙ ДЛИНЫ.

На таких графах кратчайшие пути автоматически будут элементарными, так как добавление контура может привести только к увеличению стоимости пути. В этом разделе мы рассмотрим четыре алгоритма, которые будут вычислять матрицу D расстояний между источником и всеми остальными вершинами:

- первый подходит графам самого общего вида, т.е. без контуров отрицательной длины;

- второй применяется для графов с неотрицательными весами;

- третий – для бесконтурных графов;

- четвертый на графе общего вида находит расстояния между всеми парами вершин.

Сразу возникает вопрос: зачем нужны четыре различных алгоритма, когда для решения всех этих задач было бы достаточно одного, самого первого?

Дело в том, что идет борьба за эффективность, т.е. вычислительную сложность алгоритма. Чем более специального вида граф, тем более быстрым специализированным алгоритмом решается задача о кратчайшем пути.

Прежде, чем рассматривать эти алгоритмы, обратим внимание на следующее: алгоритм выдает в качестве результата не сами пути, а матрицы расстояний. Решим следующую задачу:

зная расстояния от источника s до всех остальных вершин, найдем путь от источника до какой-то выбранной вершины t.

Если нам удастся по последней вершине t восстановить предпоследнюю (назовем ее v), то задача решена. Восстановим предпоследнюю, по ней предпредпоследнюю и так до тех пор, пока не дойдем до источника.

Предпоследняя вершина v кратчайшего пути обладает следующим свойством: D[s,t] = D[s,v] + A[v,t].

АЛГОРИТМ {Восстановление кратчайшего пути от s до t.}

Данные: Расстояния D[v] от источника s до всех остальных vÎV, фиксированная вершина t, матрица весов A[u,v], u,vÎV.

Результаты: СТЕК, содержащий путь от s до t.

1 begin

2 СТЕК:= 0; СТЕК Ü t; v:= t;

3 while v<>s do

4 begin

5 u:= первая из списка PRED[v];

6 while D[v]<>D[u]+A[u,v] do

7 u:= следующая из списка PRED[v];

8 СТЕК Ü u; v:= u;

9 end

10 end.

Так как для поиска всех вершин u происходит просмотр не более m дуг (в списках PRED), то вычислительная сложность этого алгоритма О(m). Заметим, что при наличии в графе контура нулевого веса эта процедура зацикливается, и ее следует модифицировать таким образом, чтобы исключать повторяющиеся вершины.

Вопрос. Как переделать процедуру восстановления пути так, чтобы в случае существования нескольких путей одной длины на печать выдавались все?

Ответ. Цикл (6–7) находит одну предыдущую вершину, но для печати всех путей нужно находить все такие вершины.