Задачи с линейной системой ограничений, но нелинейной целевой функцией
Множество допустимых решений таких задач всегда выпукло, так как линей- ные ограничения образуют выпуклый многоугольник в n-мерном пространстве. Однако в отличие от линейного программирования при нелинейной целевой функ- ции оптимальное решение не обязательно находится в вершине этого многогран- ника.
 Задача 2.2.1. Определить наибольшее значение функции z =
Задача 2.2.1. Определить наибольшее значение функции z =
x 2 + y 2
при усло-
вии
ì3x+ 4 y - 24£ 0
|
|
î y ³ 0.
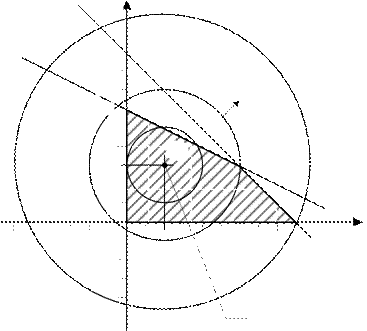
Решение. Множество допустимых решений заштриховано на рисунке 12. Если
целевой функции придавать фиксированные значения с, то будем получать окруж-
ности с центром в начале ко-
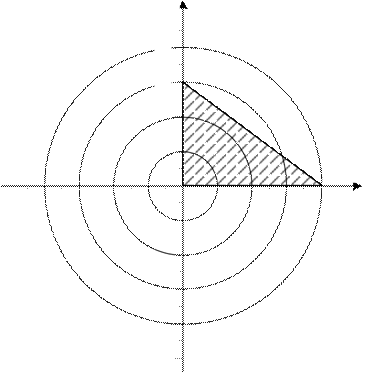 y ординат и радиусом
y ординат и радиусом
с 2 . Пусть
7 B(0;6)
 2
2
с = 1,2, … Начертим ряд окружностей (линии уровня целевой функции). Из рисунка
12 видно, что функция z =
1 A(8;0)
x 2 + y 2
достигает наиболь-
-9 -8
-7 -6 -5 -4
-3 -2
-2
1 2 3 4 5 6 7 8 x
шего значения, равного 8,в
 -3 точке A(8;0):
-3 точке A(8;0):
 -4
-4
 -5
-5
 -6
-6
 -7
-7
-8
-9
zmax= 8.
рис. 12.
Задача 2.2.2. Найти глобальные экстремумы функции
ìx + 2 y £ 12
ï
z = (x - 2)2+ ( y - 3)2 на
множестве решений системы
ïx + y £ 9
í
ïx ³ 0
ïî y ³ 0.
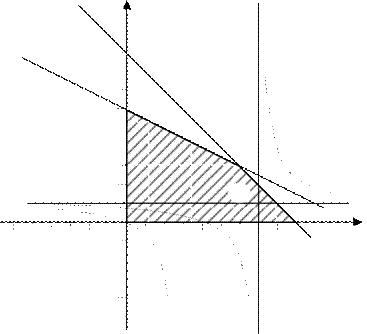
Решение. Построим многоугольник допустимых планов и несколько линий
уровня (рис. 13). Линии уровня
z = c
представляют собой окружности с центром в
 точке A(2;3) и радиусом r =
точке A(2;3) и радиусом r =
c . Из рисунка 13 видно, что
zmin= 0
достигается в
точке A(2;3), а
zmax- в точке B(9;0). Таким образом, получаем, что
zmin= 0,
zmax
= (9 - 2)2+ (0 - 3)2 = 58.
 y
y
 8
8
 7
7
6 E
4 A D
-5 -4
-3 -2
-2
-3
1 2 3 4 5 6 7 8
x
B(9;0)
-4 z
min=0
рис 13
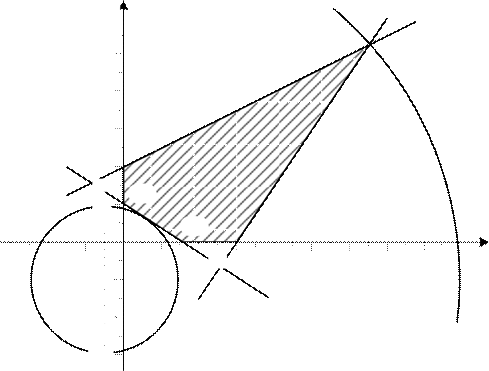
Задача 2.2.3. Найти глобальные экстремумы функции
ìx + 2 y £ 12
ï
z = (x - 7)( y -1) на мно-
жестве решений системы
ïx + y £ 9
í
ïx ³ 0
ïî y ³ 0.
Решение. Многоугольник допустимых планов мы уже строили при решении задачи 14, а линиями уровня являются равносторонние гиперболы, асимптотами
которых служат прямые x=7, y=1 (рис.14). С ростом значений z гиперболы удаля- ются от точки пересечения асимптот. Наибольшее значение z соответствует гипер- боле (нижней ветви), проходящей через точку O(0;0), а наименьшее – гиперболе,
вырождающейся в точку K(7;1). Таким образом, получаем
zmin = 0 - в точке K(7;1).
zmax= 7
в точке O(0;0),
 y
y
E
D
K
0 x
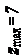
 B
B
рис 14
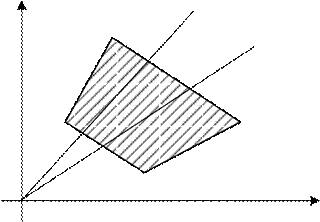
Задача 2.2.4. Графическим методом найти максимум и минимум целевой функции, если математическая модель задачи имеет вид:
z = (x1
+1)2+ (x
+ 2)2
(max, min)
| |
ï
|
î- x1+ 2x2£ 8
x1³ 0 ;
x2 ³ 0
Решение. Найдем и изобразим на плоскости x1Оx2множество решений систе- мы ограничений (рис. 15). Область допустимых решений состоит из внутренних точек многоугольника ABCDE. Линии уровня представляют собой окружности с центром в точке О1(-1; -2). Глобальным максимум находится в точке B, как самой
удаленной от точки О1. Глобальный минимум находится в точке F, в которой
окружность касается прямо проходящей через ED. Точка B является точкой пере- сечения прямых (II) и (III), для определения координат этой точки решим систему уравнений:
ì3x1- 2x2= 18
í
î- x1 + 2x2= 8.
-5 -4
x2
 10
10
-3 -2
-2
-3
-4
-5
-6
A E
D
1 2 3 4
С
5 6 7 8
9 10
B
11 12 13 14 15 16 x1
рис.15
Получим значения
x1= 13 ;
x2= 10,5. При этом
zmax
= 142 +12,52 = 352,25.
Для определения координат точки F в начале получим уравнение прямой, про- ходящей через точки E(0; 2) и D(3; 0)

 x1- 0 = x2 - 2 .
x1- 0 = x2 - 2 .
3 - 0
0 - 2
Отсюда, получим уравнение прямой ED: x
= - 2 x
+ 2.
 2 3 1
2 3 1
Угловой коэффициент этой прямой
k = - 2 .
 1 3
1 3
Найдем теперь уравнение прямой, проходящей через точку О1(-1; 2) перпен- дикулярно к прямой ED. Угловой коэффициент этой прямой k2 определим их усло-
вия перпендикулярности прямых:
k1× k2= -1. Значит,
k2=
. Уравнение прямой O1F
 2
2
запишем в виде: x
+ 2 = 3 (x
+ 1).
 2 2 1
2 2 1
Отсюда, получим уравнение прямой O1F: x
= 3 x
- 1 .

 2 2 1 2
2 2 1 2
Для определения координат точки F решим систему:
ì 2
 ïx2= - 3 x1+ 2
ïx2= - 3 x1+ 2
í
ïx = 3 x
- 1 .
Получим,
 x = 15;
x = 15;
1 13
 x = 16.
x = 16.
2 13
îï 2


2 1 2
Тогда,
zmin
æ15 ö
| |
è 13 ø
æ16 ö
| |
| |
è 13 ø
= 2548
К рассматриваемому типу нелинейных задач относятся и задачи с дробно- линейной целевой функцией. Дробно-линейной функцией называется функция вида
 z = a0+ a1x1+ a2x2+ ... + anxn .
z = a0+ a1x1+ a2x2+ ... + anxn .
b0+ b1x1+ b2x2+ ... + bnxn
Задача 2.2.5. Предприятие выпускает однородный продукт и располагает при этом четырьмя технологическими способами. При работе по этим способам в
единицу времени получается соответственно продукция
q1,
q2,
q3 ,
q4, при этом
производственные расходы в единицу времени составляют
p1,
p2 ,
p3,
p4 некото-
рых единиц. Составить математическую модель данной задачи. Найти такой план выпуска продукции, при котором себестоимость будет наименьшей и по
каждому из способов предприятие должно работать не более соответственно.
t1 ,
t2,
t3 ,
t4 часов
Решение. Пусть
x1 единиц времени предприятие работает по первой техноло-
гии,
x2- по второй,
x3-по третьей,
x4- по четвертой. Тогда общий выпуск продук-
ции составит
q1x1+ q2x2+ q3 x3+ q4x4, а общий расход будет равен
p1x1+ p2x2+ p3 x3+ p4x4.
Отношение общего расхода к общему объему выпускаемой продукции назы- вается себестоимостью продукции:
 z = p1x1+ p2x2+ p3 x3 + p4x4.
z = p1x1+ p2x2+ p3 x3 + p4x4.
q1x1+ q2x2+ q3 x3 + q4x4
Итак, на множестве решений системы ограничений
0 £ x1£ t1 ,
0 £ x2£ t2,
0 £ x3£ t3,
0 £ x4£ t4
Надо найти наименьшее значение целевой функции
 z = p1x1+ p2x2+ p3 x3 + p4x4.
z = p1x1+ p2x2+ p3 x3 + p4x4.
q1x1+ q2x2+ q3 x3 + q4x4
Задачу с дробно-линейной целевой функцией путем замены переменных мож- но свести к задаче линейного программирования, а затем решить симплексным ме- тодом. Как это делается, мы узнаем дальше, а сначала познакомимся с геометрическим смыслом и графическим способом решения задач дробно- линейного программирования.
Рассмотрим на плоскости
x1Ox2
целевую функцию:
 Выразим
Выразим
x2:
z = p1x1+ p2x2q1x1+ q2x2
zq1x1+ zq2 x2= p1x1+ p2x2
(zq2- p2)x2= ( p1- zq1)x1,
 x = ( p1 - zq1) × x
x = ( p1 - zq1) × x
|
или
x2= kx1,
где k =
p1- zq1.
 zq2- p2
zq2- p2
Уравнение
x2 = kx1
задает прямую, проходящую через начало координат. При
некотором фиксированном значении z угловой коэффициент k прямой тоже фик-
сирован, и прямая займет определенное положение. При изменении значений z
прямая
x2= k × x1
будет поворачиваться вокруг начала координат (рис. 16).
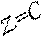
 x2
x2
0 x1
рис.16
Установим, как будет вести себя угловой коэффициент k при монотонном воз- растании z. Для этого возьмем производную от k до z:

| |
= - zq1q2 + p2q1- p1q2 + zq1q2
= p2q1- p1q2.

 dz (zq2
dz (zq2
- p2 )
(zq2
- p2)
(zq2
- p2)
| |
| |
1 .Многоугольник допустимых планов ограничен, глобальный максимум и глобальный минимум есть (рис. 17).
 x2
x2
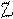
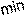 0 x1
0 x1
рис.17
2 .Множество допустимых планов ограничений не ограничено, но глобаль- ные экстремумы функцией достигаются (рис. 18).
 x2
x2
 0 x1
0 x1
рис.18
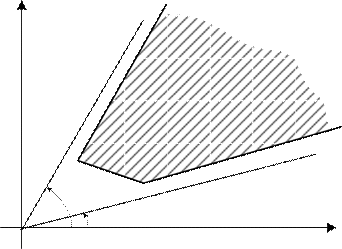
3 .Множество допустимых планов не ограничено и один из глобальных экс- тремумов не достигается (рис. 19).
При удалении точки А пересечения прямых в бесконечность, т.е. когда луч z станет параллелен получается так называемый асимптотический максимум, кото- рый может быть как конечный, так и бесконечно большим.
 B
B
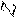
 x2
x2
A
 0 x1
0 x1
рис.19
4 .Множество не ограничено, оба экстремума асимптотические (рис.20).
 x2
x2
 0 x1
0 x1
рис.20
Задача 2.2.6.Найти глобальный максимум и минимум целевой функции
 z = 3x1- x2
z = 3x1- x2
x1+ x2
при
|
ï- x1+ 3x2£ 7
ограничениях
ï
í3x1
- x2
£ 11
ïx ³ 0
ï 1
ïîx2 ³ 0.
Решение. Строим на чертеже множество допустимых планов (рис. 21). Так как оптимум находится вращением разрешающей прямой вокруг начала координат, то сразу можно сказать, что экстремальными точками будут вершины А и В.
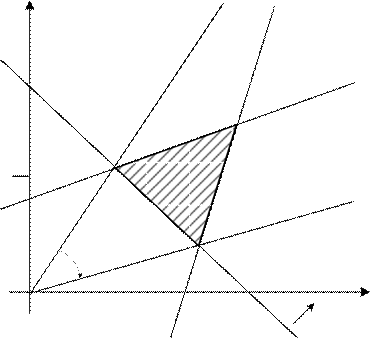
 x2
x2

 5
5
 A C
A C
 7
7
B
0 5 x1
рис.21
Воспользуемся приведенными выше рассуждениями. Выразим из выражения
для целевой функции x : x
= 3 - z × x .
 2 2 z + 1 1
2 2 z + 1 1
Теперь найдем угловой коэффициент разрешающей прямой:
k = 3 - z ;
 z + 1
z + 1
ищем
производную:
dk =

 dz
dz
- 4 . (z + 1)2
Так как производная при любом z отрицательна, то функция
Это соответствует вращению прямой по часовой стрелке.
k = 3 - z
 z + 1
z + 1
убывает.
Задача 2.2.7. Найти глобальные экстремумы (максимум и минимум), если ма- тематическая модель задачи имеет вид:
 z = 2x1- x2(max, min),
z = 2x1- x2(max, min),
x1+ x2
ì2x1- 3x2³ -13,
ï
|
î4x1 - x2£ 19,
x1 ³ 0, x2 ³ 0.
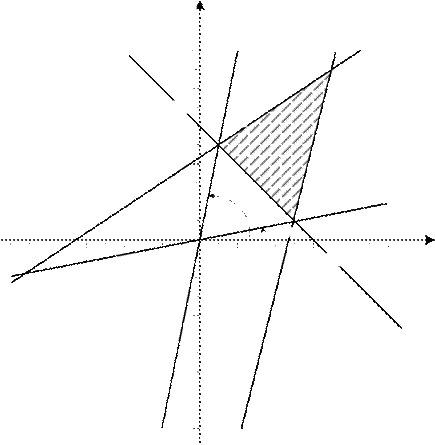
Решение. Найдем область определения допустимых значений для переменных
x1; x2
22).
определим на плоскости
x10x2множество решений системы ограничений (рис.
Областью допустимых значений (множеством решения системы неравенств)
является множество точек, расположенных внутри треугольника АВС. Выразим x2
из выражения для целевой функции
 z = 2x1- x2,
z = 2x1- x2,
x1+ x2
z × (x1+ x2) = 2x1- x2,
zx1+ zx2= 2x1- x2,
x2× (z + 1) = (2 - z) × x1,
x = 2 - z × x
2 z + 1 1
Данному соотношению удовлетворяют точки, принадлежащие прямой
2 - z
x2= k × x1
с угловым коэффициентом
k = .
 z + 1
z + 1
Значит, линиями уровня функции цели являются прямые, проходящие через
начало координат с угловым коэффициентом
k = 2 - z .
 z + 1
z + 1
Определим предельные значения угловых коэффициентов для семейства пря- мых, являющихся линиями уровня и имеющими общие точки с множеством допу-
стимых значений. Пусть угол a1
равен углу между осью
ОX1
и радиус-вектором
ОА, а угол a 2
равен углу между осью
OX 2
и радиус-вектором ОВ, тогда должно
выполняться условия
tga1£ k £ tga2.
 x2
x2
| |
|
I 2 ?2 A
?1
-10 -9
-8 -7
-6 -5
-4 -3
-2
-2
-3
-4
-5
-6
-7
-8
-9
-10
1 2 3 4 5 6 7 8 9 10 x1
II
III
Рис.22
Найдем координаты точки А, для этого решим систему уравнений
ìx1+ x2= 6,
í
î4x1- x2= 19.
Получим
x1= 5;
x2= 1. значит, tga1= .
 5
5
Найдем координаты точки В, для этого решим систему уравнений
ì2x1- 3x2= -13
í
îx1 + x2= 6.
Получим,
x1= 1;
x2= 5. Значит, tga2= 5 .


 Таким образом, имеем неравенства
Таким образом, имеем неравенства
1 £ k £ 5 ,
1 £ 2 - z £ 5
Решим систему неравенств
5 5 z + 1
ì1 £ 2 - z
ì6z - 9 £ 0
ï5 z + 1
í
ï z + 1
í
ï 2 - z £ 5;ï6 z + 3 £ 0.
ïî z + 1
îï z + 1
Каждое из этих неравенств решаем методом интервалов. Общее решение си-
стемы неравенств:
- 0,5 £ z £ 1.5
Таким образом,
zmin
= -0.5 ; это значение достигается в точке А(5; 1).
zmax = 1.5 ; это значение достигается в точке В(1; 5).
