Переходный процесс при подключении катушки индуктивности в цепи с источником постоянной ЭДС

Проанализируем переход­ный процесс в цепи при замыкании ключа К момент времени t = 0 (рис. 4, а), выполнив последовательно все этапы расчета классиче­ским методом. В дальнейшем для сокращения решений математические операции отдельных этапов будем совмещать.

1. При выбранных положительных направлениях тока i и напряже­ний u_r и u_L составим систему уравнений, описывающих состояние це­пи на основе второго закона Кирхгофа, закона Ома и Закона электро­магнитной индукции:

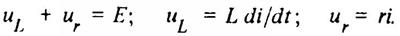(12)

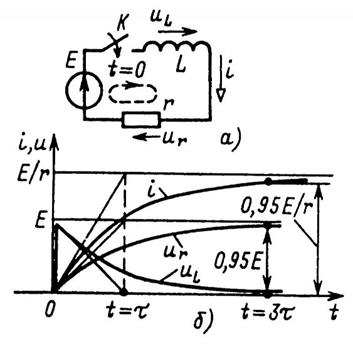
Рис. 4

Исключая из системы уравнений (12) переменные u_r и u_L, получаем неоднородное дифференциальное урав­нение переходного процесса первого порядка

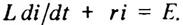(13)

2. Найдем общее решение неоднородного дифференциального урав­нения (13) как сумму его частного решения и общего решения соот­ветствующего однородного дифференциального уравнения:

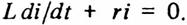(14)

Частным решением неоднородного дифференциального уравнения первого порядка (14) является постоянный ток (нет изменения тока и di/dt = 0) после окончания переходного процесса (который теорети­чески продолжается бесконечно), т. е.

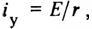(15)

называемый установившимся током.

Непосредственной подстановкой легко убедиться, что это частное решение удовлетворяет неоднородному дифференциальному уравне­нию (13).

Общее решение однородного дифференциального уравнения (14) называется свободным током

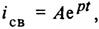(16)

где р = -r/L - корень характеристического уравнения

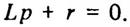
Таким образом, с учетом (15) и (16) общее решение неоднородного дифференциального уравнения (13) имеет вид

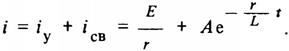(17)

2. Определим постоянную интегрирования А в общем решении (17). Для этого обратимся к закону коммутации для индуктивного эле­мента в момент времени замыкания ключа t = 0. Так как ток в индуктивном элементе не может измениться скачком, а до коммута­ции, т. е. в момент t =0_ , он был равен нулю, то

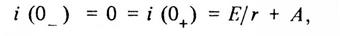
откуда

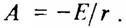
Подставив это значение постоянной А в (17), получим закон нара­стания тока в цепи (рис. 4, б):

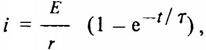(18)

где τ= L/r имеет размерность времени (Гн/Ом или с) и называется постоянной времени цепи. Постоянная времени определяет скорость нарастания тока и равна времени, за которое ток i достиг бы уста­новившегося значения i_у = Е/r , если бы скорость его изменения оста­валась неизменной и равной начальному значению скорости di/dt|_t=0+ = E/L.

Переходный процесс часто можно считать практически закончив­шимся через интервал времени 3τ с момента коммутации, когда ток достигнет значения i(3τ) =0,95Е/r.

Так как зависимость тока от времени найдена (18), то нетрудно определить и зависимости от времени напряжений на резистивном и индуктивном элементах (рис. 4,б):

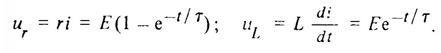
При 0 ≤ t < τ скорость изменения тока в цепи можно считать приближенно постоянной и равной 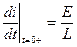. Следовательно, в этом интервале времени приближенно напряжение на резистивном элементе равно

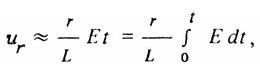
т. е. пропорционально интегралу напряжения источника ЭДС Е. Такую цепь принято называть интегрирующей цепью.

При действии на входе цепи источника изменяющейся ЭДС е может оказаться, что в некоторые интервалы времени переходного процесса u_r>>u_L. Для этих интервалов времени ток в цепи i=е/r , а напряжение на индуктивном элементе

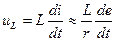
приближенно пропорционально скорости изменения напряжения источника ЭДС е. Имея это в виду, эту же цепь называют дифференцирующей цепью.