Открытая транспортная задача
Постановка задачи
Изменим условие задачи 4 следующим образом: допустим, что потребность первого завода в кирпиче возросла вдвое и составила 140 ед. кирпича в день. Остальные данные остались неизменными.
Таблица 12
| Стоимость перевозки 1 усл. ед. кирпича с завода к строящемуся объекту | Возможности заводов | ||||
 Объекты Заводы Объекты Заводы | |||||
| I | |||||
| II | |||||
| III | |||||
| Потребность объектов в кирпиче |
Данная задаче уже является открытой, т.к. 140+80+60+9>100+150+50, т.е. потребности превышают запасы на 160 ед.
Введем нового поставщика - IV завод с возможностью 160 ед.
Так как груз от фиктивного поставщика к фиктивному потребителю не перевозится, то стоимость перевозок полагается равной нулю.
Таблица 12 примет вид:
Таблица 13
| Стоимость перевозки 1 усл. ед. кирпича с завода к строящемуся объекту | Возможности заводов | ||||
 Объекты Заводы Объекты Заводы | |||||
| I | |||||
| II | |||||
| III | |||||
| IV | |||||
| Потребность объектов |
Данная задача уже является закрытой и решается аналогично задаче
Применение транспортных моделей к решению экономических задач
Алгоритм и методы решений транспортной задачи могут быть применены для решения некоторых классов экономических задач. К таким задачам относятся:
· Задача о назначениях. Она позволяет определить какой механизм и на какую работу надо назначить, чтобы добиться максимальной производительности или минимизировать затраты времени.
· Задача о закреплении самолетов за воздушными линиями.
· Оптимальное закрепление за станками операций по обработке деталей и др.
Задача о назначениях
Постановка задачи
Мастер должен расставить трех рабочих для выполнения трех операций. Причем, каждый рабочий должен выполнять только одну операцию и каждая операция должна выполняться только одним рабочим. Известно сколько минут в среднем тратит каждый из рабочих на выполнение каждой операции. Данные представлены в таблице:
| Работники | Работы | ||
| 10 | 12 | 14 | |
| 11 | 13 | 14 | |
| 10 | 9 | 12 |
Как распределить рабочих по операциям, чтобы минимизировать суммарные затраты рабочего времени?
Решение
I этап: Составление математической модели
Элементы модели
Переменные (неизвестные) задачи
Так как в задании требуется распределить рабочих по операциям, то введем переменные 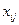 , которые будут принимать только два значении:
, которые будут принимать только два значении:
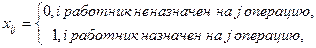
i=1,2,3, j = 1,2,3,.
В итоге мы имеем 9 неизвестных.
Целевая функция V
Цель задачи – минимизировать суммарные затраты рабочего времени. Т.к. время выполнения каждым рабочим каждой операции известно, то можно составить целевую функцию.
V будет иметь вид:
V=10*x11+12*x12+14*x13+
+11*x21+13*x22+14*x23+
+10*x31+9*x32+12*x33 (мин.)
Ограничения
Так каждый рабочий должен выполнять только одну операцию и каждая операция должна выполняться только одним рабочим, то на неизвестные 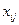 накладывается ряд ограничений:
накладывается ряд ограничений:
Каждый рабочий выполняет только одну операцию
x11+x12+x13=1, (22)
x21+x22+x23=1, (23)
x31+x32+x33=1, (24)
Каждая операция выполняется только одни рабочим
x11+x21+x31=1, (25)
x12+x22+x32=1, (26)
x13+x23+x33=1, (27)
xi –двоичные (28)
Примечание:
Ограничение 7 представляют собой следующие условие:
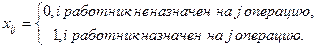
| Неизвестные | |
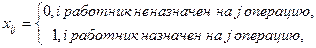 i=1,2,3, j = 1,2,3,. i=1,2,3, j = 1,2,3,. | |
| Целевая функция | Ограничения |
| V=10*x11+12*x12+14*x13+ +11*x21+13*x22+14*x23+ +10*x31+9*x32+12*x33 (мин.) | x11+x12+x13=1, x21+x22+x23=1, x31+x32+x33=1, x11+x21+x31=1, x12+x22+x32=1, x13+x23+x33=1, xi –двоичные |
Численное решение задачи в Excel аналогично решению транспортной задачи.
