Общая постановка задачи линейного программирования
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ
по дисциплине «Экономико-математические методы и модели»
для студентов экономических специальностей
Часть I
Одобрено
Учебно-методическим
Советом университета
Составитель: Сосина Н.А.
Тольятти 2008
Утверждено на заседании кафедры
«Высшая математика»
Протокол № __ от ___________2008 г.
Зав. Кафедрой: Т.В. Никитенко
Утверждено Научно-методическим Советом
По специальности _____________
Протокол №__от____________2008 г.
Председатель НМС: __________
Рецензент: ст. препод. Т.Ю. Матвеева
СОДЕРЖАНИЕ
Введение__________4
§1. Примеры математического моделирования__________5
§2. Графический метод решения задачи
линейного программирования_____________________15
§3. Симплексный метод _____________________________26
Понятие о двойственных задачах
Линейного программирования_____________________36
Транспортная задача _____________________________41
§6. Элементы теории игр _____________________________55
§7. Решение оптимизационных задач
в рамках MS Excel _______________________________71
Ответы _________76
Варианты типовых расчетов _______________________78
Литература ______85
Введение
Согласно экономической теории, в экономике действуют устойчивые количественные связи, поэтому возможно их строгое формализованное изложение путем создания математических моделей.
Модель – это объект, который замещает оригинал и отражает наиболее важные для данного исследования черты и свойства оригинала. Модель, представляющая собой совокупность математических соотношений, называется математической.
Построение экономико-математической модели происходит поэтапно:
1) формулируются предмет и цели исследования;
2) выявляются основные элементы модели;
3) словесно описывается взаимосвязь между элементами модели;
4) модель формализуется с помощью математических символов;
5) проводятся расчеты по построенной математической модели с привлечением математических методов;
6) анализируются полученные результаты.
Экономико-математические модели позволяют выявлять особенности функционирования экономического объекта и на основе этого прогнозировать будущее изменение объекта при изменении каких-либо параметров.
Примеры математического моделирования
В параграфе §1 рассмотрим четвертый этап построения моделей: формализацию с помощью математических символов.
Остановимся на построении модели задачи линейного программирования.
Общая постановка задачи линейного программирования
На практике постоянно встречаются такие ситуации, когда достичь какого-то результата можно не одним, а многими различными способами. Естественно, что при большом числе решений, выбирается наилучшее.
Математически это обычно сводится к нахождению наибольшего или наименьшего значения некоторой функции, т.е. к задаче найти max (min)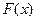 
при условии, что переменная пробегает некоторое заданное множество 
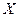. Задача может быть сформулирована следующим образом:
,
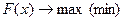
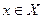где 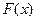– целевая функция (показатель эффективности),
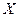- допустимое множество значений 
.
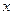Чаще всего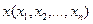 
это n – мерный вектор, а 
.
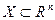Точку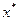 
, в которой 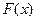достигает 
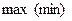, и при этом 
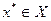называют оптимальным решением, таких точек может быть множество.
Если целевая функция и ограничения заданы при помощи линейных функций, то задача называется задачей линейного программирования (ЛП).
В общем виде задача линейного программирования формулируется следующим образом: дана линейная функция
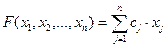(1.1)
и система m линейных уравнений и неравенств с n переменными:
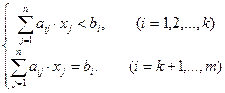(1.2)
Необходимо найти такое решение системы ограничений (1.2), при котором линейная функция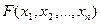 
принимает оптимальное (т.е. максимальное или минимальное) значение.
Задача линейного программирования, в которой система ограничений (1.2) состоит только из неравенств, называется стандартной задачейЛП. Если же задача ЛП содержит ограничения (1.2) только в виде равенств, то ее называют канонической задачей.