Математическое обеспечение САПР (часть 1)
К математическому обеспечению относят математические модели, численные методы, алгоритмы выполнения проектных процедур.
Различают 4 уровня математического обеспечения:
1.Микроуровень;
2.Макроуровень;
3.Функционально-логический уровень;
4.Системный уровень.
На микроуровне создаются математические модели элементов (ММЭ) электронных и электрических схем: логических элементов, усилителей, трансформаторов, реле, двигателей и т.д. К микроуровню относят уравнения математической физики, представляющие собой математическое описание полей физических величин, что требуется при анализе прочности строительных сооружений (оболочек, колонн, фундаментов), машиностроительных деталей, моделировании электромагнитных полей, потоков частиц, процессов в жидких средах и т.д. Математические модели математической физики обычно представляют собой дифференциальные уравнения в частных производных вместе с краевыми условиями.
Макроуровень обычно представлен системами алгебраических и обыкновенных дифференциальных уравнений, отражающих связи отдельных компонентов системы.
Когда сложность математической модели превышает некоторый предел, переходят на функционально-логический уровень.
На функционально-логическом уровне в непрерывных системах используют аппарат передаточных функций, а в дискретных системах – аппарат логических функций.
Для более сложных объектов: производственных предприятий, вычислительных сетей, социальных систем используют аппарат системного уровня: теория массового обслуживания, теория сетей Петри, теория принятия решений и т.д.
Требования, предъявляемые к математическим моделям:
1.Адекватность;
2.Точность;
3.Экономичность.
Под адекватностью понимают способность модели отражать заданные свойства объекта с приемлемой точностью. Под точностью понимают степень соответствия оценок свойств модели и объекта.
Экономичность (вычислительная эффективность) определяется затратами ресурсов, требуемых для реализации модели. Ресурсами являются затраты машинного времени и памяти.
Адекватность оценивается перечнем отражаемых свойств и областью адекватности. Область адекватности это область в пространстве параметров, в пределах которой погрешности модели остаются в допустимых пределах. Например, область адекватности модели электронного элемента обычно выражает допустимые для применения модели диапазоны изменения моделируемых температур, напряжений, частот. Аналогичны требования по точности и экономичности используются при выборе численных методов решения уравнений модели.
Процедуры формирования моделей.
Формирование модели происходит в два этапа:
1.Разработка моделей отдельных компонентов;
2.Формирование модели объекта из моделей компонентов.
Созданные модели компонентов включаются в библиотеки программ анализа систем.
Как правило, модели компонентов разрабатываются специалистами в прикладных областях техники. Обычно в помощь разработчику моделей систем предлагаются методики и вспомогательные средства. Например, модели измерительных приборов с интерфейсом, приближенным к реальному виду приборов (осциллограф, источники сигналов и т.д.).
На втором этапе выполняется формирование модели системы с использованием
библиотечных моделей компонентов. Как правило, эта процедура выполняется автоматически по алгоритмам, включённым в заранее разработанные программы анализа. Например, программы анализа работы схемы во временной и частотной областях
Исходные уравнения моделей.
Для формирования математических моделей объектов исходными являются компонентные и топологические уравнения. Компонентными уравнениями называют
уравнения математических моделей элементов (ММЭ). Топологические уравнения
описывают взаимосвязи в составе моделируемой системы. В совокупности компонентные и топологические уравнения конкретной физической системы образуют собой исходную математическую модель системы (ММС) .
Примеры компонентных и топологических уравнений.
Электрические системы.
Переменными являются напряжения и токи. Компонентами могут быть простые двухполюсники и более сложные многополюсные компоненты.
К простым двухполюсникам относятся сопротивление, ёмкость и индуктивность,
Характеризуемы параметрами R, C, L простых двухполюсников:
Для R: u = iR,
Для C: I = du/dt,
Для L: u = L(di/dt).
Эти модели лежат в основе моделей более сложных компонентов.
Топологические уравнения выражают законы Кирхгофа для напряжений и токов,
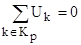 ,
, 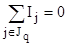 ,
,
где Kp – множество номеров элементов p-го контура, Jq – множество номеров токов, входящих в q-ю узловую точку.
Примеры компонентных уравнений механики: уравнения 2 закона Ньютона, уравнения закона Гука.
Численные методы решения обыкновенных дифференциальных уравнений.
Каждое дифференциальное уравнение имеет бесконечное множество решений,
которые отличаются друг от друга константами. Для однозначного определения решения требуется задать начальные или граничные условия. Количество таких условий должно совпадать с порядком дифференциального уравнения или системы.
В зависимости от вида дополнительных условий различают:
Задачу Коши – все дополнительные условия заданы в одной (чаще всего в начальной) точке интервала;
Краевую задачу – дополнительные условия указаны на границах интервала.
Различают точные (аналитические) и приближённые (численные) методы решения дифференциальных уравнений. Большое количество уравнений может быть решено
точно. Но есть уравнения, и особенно их системы, для решения которых точное решение записать нельзя. Поэтому широкое распространение получили численные методы решения обыкновенных дифференциальных уравнений, которые в Matlab
реализованы с помощью специальных функций.
Рассмотрим численные методы решения обыкновенного дифференциального уравнения первого порядка для следующей задачи Коши. Найти решение дифференциального уравнения:
x' = f(x, t) ,
удовлетворяющее начальному условию:
x(t0) = x0.
Иными словами, требуется найти интегральную кривую, проходящую через заданную точку. Для дифференциального уравнения n-го порядка:
x(n) = f(t, x, x’, x’’, …, x(n-1))
задача Коши состоит в нахождении решения x = x(t), удовлетворяющего уравнению и начальным условиям:
x(t0) = x0, x’(t0) = x’0, …, x(n-1)(t0) = x (n-1) 0.
Рассмотрим основные численные методы решения задачи Коши.
Метод Эйлера
На интервале [t0, tn], выбрав достаточно малый шаг h, построим систему равноотстоящих точек:
h = (tn - t0)/n, ti = t0 + ih, i = 0, 1, 2,…, n,
тогда:
xi+1 = xi + h*f(xi, ti), i = 0, 1, 2,…, n.
Такой процесс нахождения значений функции xi в узловых точках ti называется методом Эйлера. В связи с недостаточной точностью этого метода разработаны его модификации.
Модифицированный метод Эйлера
Согласно этому методу вначале вычисляют промежуточные значения
tp = ti + (h/2), xp = xi+ (h/2)f(ti , xi)
после чего находят значение xi+1 по формуле:
xi+1 = xi + hf(xp, tp), i = 0, 1, 2,…,n
Метод Рунге-Кутта
Рассмотренные методы Эйлера являются частными случаями явного метода
Рунге- Кутта k- го порядка. В общем случае формула вычисления очередного приближения методом Рунге- Кутта имеет вид:
xi+1 = xi + h  ( ti , xi, h), i = 0, 1, 2,…, n.
( ti , xi, h), i = 0, 1, 2,…, n.
Функция  ( t, x, h) приближает отрезок ряда Тейлора до k- го порядка и не содержит
( t, x, h) приближает отрезок ряда Тейлора до k- го порядка и не содержит
частных производных f(t, x). Метод Эйлера является методом Рунге- Кутта первого порядка (k = 1) при 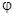 ( t, x, h) = f(t, x).
( t, x, h) = f(t, x).
Метод Рунге-Кутта второго порядка
Семейство методов Рунге-Кутта второго порядка имеет вид:
xi+1 = xi + h{(1-а) f(ti , xi) +af(ti + 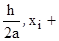
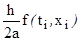
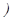 }, i = 0, 1, 2,…, n.
}, i = 0, 1, 2,…, n.
При а = 1 получаем модифицированный метод Эйлера.
Рассмотренные методы Рунге-Кутта относятся к классу одношаговых методов, в которых для вычисления значения очередной точке xk+1 нужно знать значение в предыдущей точке xk. Ещё один класс решения задачи Коши - многошаговые методы, в которых используются точки xk-3, xk-2, xk-1, xk для вычисления xk+1. В многошаговых
методах первые четыре начальные точки (t0 , x0), (ti , xi), (t2 , x2) (t3 , x3) должны быть получены заранее любым из одношаговых методов. Наиболее известным многошаговым методом является метод прогноза-коррекции Адамса.
Для решения дифференциальных уравнений и систем в Matlab предусмотрены следующие фунукции:
ode45(f, interval, x0);
ode23(f, interval, x0);
ode113(f, interval, x0);
ode15s(f, interval, x0);
ode23s(f, interval, x0);
ode23t(f, interval, x0);
ode23tb(f, interval, x0).
Входными параметрами этих функций являются:
f - вектор-функция для вычисления правой части уравнения или системы уравнений;
interval – массив из двух чисел, определяющий интервал интегрирования уравнения или системы уравнений;
x0 – вектор начальных условий.
В функции ode45 реализован метод Рунге-Кутта 4-5 порядка точности, в функции ode23 также реализован метод Рунге-Кутта, но 2-3 порядка, а функция ode113 реализует метод Адамса.
Пример:
Решить задачу Коши:
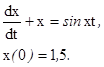
Чтобы дифференциальное уравнение вида 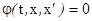 можно было решить посредством функций Matlab, его необходимо преобразовать к виду y =F(t, x) и записать в виде М-файла
можно было решить посредством функций Matlab, его необходимо преобразовать к виду y =F(t, x) и записать в виде М-файла

В рабочем окне программы Matlab записывается команда, атрибуты которой содержат имя функции, интервал интегрирования, начальные условия
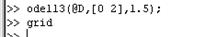
. Результаты решения представлены на рис. 1.
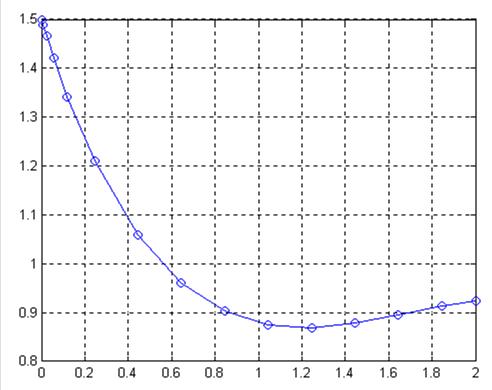
Рис. 1.
