Поиск в глубину в графе
Существует много различных алгоритмов, в основе которых лежит систематический перебор вершин графа, при котором каждая вершина просматривается ровно один раз. Будем рассматривать такие методы обхода или поиска в графе, что:
а) алгоритм решения легко «погружается» в этот метод;
б) каждое ребро графа анализируется число раз, ограниченное константой.
Опишем классический метод поиска в неориентированном графе – метод поиска в глубину(depth first search) (рис. 8.8).
Общая идея следующая. Начинаем поиск с некоторой фиксированной вершины k (корня). Затем выбираем одну из смежных (соединенных ребрами) с ней вершин. Назовем эту вершину u. Далее процесс поиска повторяется от u.
Пусть на каком-то этапе мы находимся в вершине v. Если среди ее соседей есть хотя бы одна новая (еще непросмотренная) вершина w, то просматриваем ее. После этого w перестает быть новой, и дальнейший поиск продолжаем с w.
Если же у вершины v нет ни одной новой «соседки», то говорим, что v использована, и возвращаемся на шаг назад– в вершину, из которой попали в v. Просмотренные, но еще не использованные вершины накапливаются в стеке. Использованные вершины удаляются из стека. Когда стек опустеет, то у связного графа будут просмотрены все вершины, у несвязного – компонента связности, содержащая вершину k.
| |
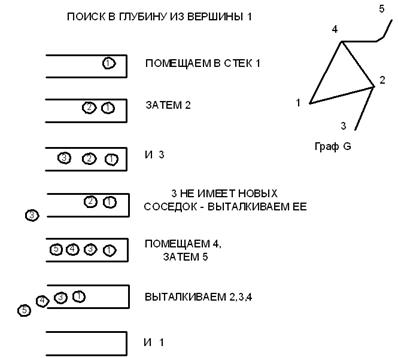
Рис. 8.8. Поиск в глубину из вершины 1
Вопрос. Когда следует прервать работу алгоритма, если мы ищем путь от 1 до 5? Где находится путь?
Поиск в глубину можно записать с помощью рекурсивной процедуры GL.
Логический массив НОВЫЙ – глобальная переменная.
1 procedure GL(v) {поиск в глубину из вершины v}
2 begin
3 НОВЫЙ[v]:= ложь;
3 for u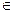 
ЗАПИСЬ[v] do {перебор всех соседей v}
4 if НОВЫЙ[u] then GL[u]
5 end; {v использована}
Поиск в глубину в произвольном (необязательно связном) графе проводится согласно следующему алгоритму:
1 begin
2 for v 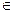V do НОВЫЙ[v]:= истина ; {инициализация}
3 for v 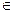V do {перебор всех вершин графа}
4 if НОВЫЙ[v] then GL(v)
5 end. {поиск окончен, все вершины просмотрены}
Покажем теперь, что этот алгоритм просматривает каждую вершину в точности один раз и сложность его порядка O(n+m).
Первый вызов GL(v) для некоторой вершины v влечет за собой просмотр всех вершин компоненты связности графа, содержащей v. Это обеспечивает цикл 3 процедуры GL: после просмотра v будет вызвана GL для всех ее новых соседей.
Каждая вершина просматривается ровно один раз – просматриваются только новые вершины, сразу после просмотра НОВЫЙ[v]:= ложь.
Гарантия того, что будут просмотрены все вершины – цикл 3 основного алгоритма.
Оценим теперь вычислительную сложность алгоритма.
Циклы 2 и 3 основного алгоритма содержат n шагов, не считая вызовы процедуры GL. Строка 2 процедуры GL для всех вызовов повлечет O(n) шагов. Полное число шагов цикла 3 процедуры GL для всех рекурсивных вызовов будет порядка m – числа всех ребер, так как от вершины к ее соседям мы двигаемся по ребрам.
Суммарная сложность алгоритма О(n+m).
В связи с важностью поиска в глубину для проектирования алгоритмов на графах представим также нерекурсивную версию процедуры GL.
Рекурсия устраняется стандартным способом: каждая просмотренная вершина помещается в СТЕК и удаляется из стека после использования.
1 procedure GL_1(v); {поиск в глубину,начиная с v}
2 begin
3 СТЕК:= NIL; СТЕК <= v; {v помещается в СТЕК}
4 НОВЫЙ[v]:= ложь;
5 while СТЕК do
6 begin
7 verh:= top(СТЕК); {читаем верхний элемент}
{будем искать первую новую «соседку» элемента verh}
8 if НАЧАЛО[verh]=nil then b:= ложь
9 else b:= NOT(НОВЫЙ[НАЧАЛО[verh]^.uzl]);
{НАЧАЛО[verh]^.uzl-номер первой вершины в списке
ЗАПИСЬ[verh]}
10 while b do
11 begin
12 НАЧАЛО[verh]:= НАЧАЛО[verh]^.next;
{переводим указатель НАЧАЛО на следующую запись в
списке ЗАПИСЬ[verh]}
13 if НАЧАЛО[verh]=nil then b:= ложь
14 else b:= NOT(НОВЫЙ[НАЧАЛО[verh]^.uzl])
{проверяем, будет ли вершина следующей записи
новой}
15 end;
16 if НАЧАЛО[verh]=nil then {найдена новая
вершина!}
17 begin
18 verh:= НАЧАЛО[verh]^.uzl;
19 СТЕК <= verh; {новая вершина помещена в СТЕК}
20 НОВЫЙ[verh]:= ложь
21 end
22 else {вершина verh использована}
23 verh <= СТЕК {удалить verh из СТЕКа}
24 end {while СТЕК <> NIL}
25 end; {procedure GL1}
Корректность процедуры GL_1 доказывается аналогично GL.
Ответ.Когда 5 попадет в стек. В стеке.