Краткие теоретические сведения. Оптимизация – это целенаправленная деятельность, заключающаяся в получении

Оптимизация – это целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.

Обычно оптимизируемая величина связана с экономичностью работы рассматриваемого объекта. В общем случае объектом может считаться любой производственный комплекс: аппарат, агрегат, цех, завод, комбинат, отрасль промышленности. Оптимальный, или наилучший, вариант работы объекта должен измеряться количественной мерой – критерием оптимальности.

Критерий оптимальности – количественная оценка оптимизируемого качества. Это главный признак, по которому судят о том, насколько хорошо функционирует данная система, работает данный процесс.

На основании выбранного критерия оптимальности составляется так называемая целевая функция F(x), представляющая собою зависимость критерия оптимальности от параметров, влияющих на его значение. Вид критерия оптимальности (или целевой функции) определяется конкретным содержанием решаемой задачи оптимизации.

Формулировка задачи оптимизации в общей постановкезаключается в определении значений управляющих параметров, оптимизирующих принятый показатель качества – критерий оптимальности, который имеет максимально или минимально возможную величину, при условии, что выполняются ограничения на переменные, накладываемые технологическими, эксплуатационными, конструктивными требованиями.

Для решения задач оптимизации необходимо:

1. Составить математическую модель объекта оптимизации;

2. Выбрать критерий оптимальности и сформировать функцию цели (целевая функция может быть как без ограничений, так и с ограничениями на значения отдельных параметров);

3. Определить управляющие параметры и их возможные ограничения;

4. Выбрать и реализовать метод оптимизации, который позволит найти экстремальные значения искомых величин.

Процедура решения задачи оптимизации процессов включает установление (или выбор) управляющих параметров (факторов) и их количества, путем изменения которых возможно управлять процессом и оптимизировать его (это может быть температура, давление, время, состав исходной смеси и др.).

Остальные параметры при этом не регулируются, хотя их значения, учитывают при определении оптимальных условий.

Ограничения на управляющие параметры– технологические величины, которые в процессе работы агрегата (аппарата) не должны выходить из предписываемых технологией допусков.

Выделяют ограничения типа равенств и типа неравенств. Ограничения типа равенств устанавливают определенное значение того или иного параметра

h_i=a_i

Переменную h_i можно рассматривать как контролируемую и нерегулируемую (состав сырья, размеры аппаратов и т. д.)

Ограничения типа неравенств определяют пределы, в которых допустимо изменение входных переменных X процесса

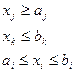
Все методы решения оптимальных задач подразделяются на следующие основные группы.

1. Аналитические методы. Их применяют, когда мы можем продифференцировать целевую функцию и найти ее экстремум.

2. Методы математического программирования (линейного, динамического, нелинейного). Для их применения нужно, чтобы можно было рассчитать значение целевой функции.

3. Методы экспериментальной оптимизации, применяют, если вид целевой функции неизвестен. Тогда проводят планирование и реализацию эксперимента таким образом, чтобы в результате достичь района оптимума.

Известны также комбинированные методы, сочетающие некоторые достоинства отдельных методов из различных групп.

Поиск оптимума численными методами.Суть численных методов: вычисляется ряд значений F при различных значениях аргументов; сопоставление этих значений показывает, в каком направлении нужно двигаться в пространстве факторов, чтобы приближаться к оптимуму.

1. Оптимизация переборомприменяется, если число возможных вариантов конечно. Рассчитывают целевую функцию для всех возможных вариантов и выбирают наибольшее (или наименьшее) значение.

2. Сканирование– метод, близкий к перебору, но применяемый к непрерывным функциям.

Рассмотрим для примера одномерное сканирование – случай, когда ищем максимум целевой функции от одного фактора (поиск минимума осуществляется точно так же).

Зададим пределы изменения фактора х от а до b. Здесь а и b – ограничения, которые можно установить в любой реальной задаче.

Данный интервал [а, b], на котором производится поиск экстремума целевой функции называется интервал неопределенности. Задача поиска экстремума сводится к сужению интервала неопределенности. Методом сканирования она решается следующим образом (рисунок 1):

Выберем целое число q – количество значений целевой функции, которое придется рассчитывать. Рассчитаем интервал Δх

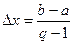
Отложим от точки а до точки b интервалы Δх (рисунок 1). Границы каждого интервала назовем узлами; на рисунке 1 каждый узел – обозначен крестиком.

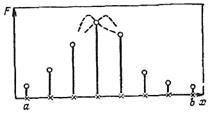
а, b – границы интервала неопределенности.

Рисунок 1 – График исследования функции сканированием:

В каждом узле расссчитаем F(х) (см. точки на рис. 1). Теперь принимают за максимум наибольшее из полученных значений – на рисунке это 4–я точка слева. К концу расчета интервал неопределенности δ составит 2Δх: истинный максимум может лежать либо справа, либо слева от полученной наилучшей точки (пунктиры на рис.1).

Формула определяет эффективность метода

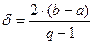
Методы направленного поиска.Методы направленного поиска более эффективны, но не обладают той универсальностью, которой отличается сканирование. Их эффективность связана с тем, что продвижение в факторном пространстве происходит в сторону искомого экстремума. Но направленность поиска имеет следующее основное требование – условие унимодальности функции, т.е. функция, должна иметь в допустимой области только один экстремум нужного знака (один максимум, если ищем максимум, один минимум в противоположном случае).

При выборе метода поиска экстремума различают два основных случая: 1) F зависит только от одного фактора, F=F(x): тогда говорят об одномерном поиске;2) факторов больше одного – многомерный поиск. Рассмотрим метод одномерного поиска (метод дихотомий) и три – многомерного – покоординатный спуск, градиентный метод, метод случайного поиска.

Дихотомия. Как и при описании сканирования, рассмотрим поиск максимума на отрезке [а, b], показанном на рисунке 2.

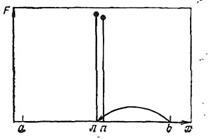Рисунок 2 – График поиска максимума методом дихотомий.

Разделим отрезок пополам – точка л(левая) на рисунке. Рассчитаем значение F=F(л) в этой точке. Выберем малое приращение фактора, равное ε, и поставим на отрезке правую точку n=л+ε. Рассчитаем F(n). Поскольку F(л)>F(n), как изображено на рисунке 2, можно утверждать, что, если F(x) унимодальна, то максимум находится в левой половине отрезка.

Отбросим правую половину отрезка (на ней максимума нет). Для этого правый конец – точку b – перенесем в точку л. Точку л обозначим через b.На рисунке 2 этот перенос обозначен стрелкой. (Разумеется, если бы было F(л)<F(n), то точку л мы перенесли бы точку а).

После того, как правый конец отрезка перенесен, задача вернулась к исходным условиям: задан отрезок от а до b, на котором нужно найти максимум. Поэтому проводится следующий цикл расчета, ничем не отличающийся от предыдущего, кроме значения b. Такой алгоритм (расчет слагается из одинаковых циклов, различающихся лишь начальными условиями) называют итерационным. Останавливают итерации, когда интервал неопределенности окажется меньше ε:

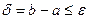
Эффективность алгоритма дихотомии определяется так: каждая пара расчетов (точки л и n) уменьшает отрезок [а, b] вдвое. Обозначим исходный отрезок индексом исх. Если сделать q расчетов (q – четное), то

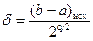
Покоординатный спуск. Выбираются координаты начальной точки поиска х_1н и х_2н, единичные приращения обоих факторов (шаги) H₁ и H₂, а также малые приращения факторов ε₁ и ε₂.

Рассчитывается значение F (х_1н, х_2н) в точке 1 (рисунок 3). Далее, не меняя величины х₂, начинаем двигаться вдоль оси x₁, давая на каждом шаге этому фактору приращение H₁ (или –H₁, в зависимости от того, при движении в какую сторону будет наблюдаться рост F). На каждом шаге – в точках 2, 3, 4 и т.д. – проводится расчет F. Шаги продолжаются до тех пор, пока продолжается рост F. Неудачными будем считать те шаги, на которых получено меньшее значение F, чем на предыдущих; на рисунке они обозначены крестиками. После первого неудачного шага (точка 6) возвращаемся в предыдущую точку (в данном случае – в точку 5), фиксируем величину x₁ и начинаем изменять х₂, давая ему приращения Н₂ или –H₂ (точки 7, 8, 9, 10).

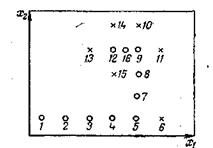
о – удачные шаги; х – неудачные шаги.

Рисунок 3. График движения в пространстве факторов при оптимизации

методом покоординатного спуска

Затем снова движемся вдоль оси x₁ (точки 11, 12, 13), снова меняем направление (точки 14, 15) и т. д. На рисунке 3 изображена ситуация, когда из точки 12 двигаться некуда: во всех окружающих точках (9, 13, 14, 15) значение F меньше, чем в данной. Это значит, что мы уже приблизились к максимуму и прежние крупные шаги из точки 12 переносят нас через него. Поэтому уменьшаем шаги (например, вдвое – см. точку 16) и продолжаем поиск уменьшенными шагами. Уменьшение шага может производиться неоднократно. Но в тот момент, когда уменьшенные шаги оказываются меньше, чем соответственно ε₁ и ε₂, считают, что максимум зафиксирован достаточно точно и можно закончить расчет, приняв лучшую точку за оптимум.

Задача. Задана целевая функция:

1. F(x)=-12∙x+2∙x²

найти значение x при котором F(x) будет минимальна. Поиск оптимума осуществить с использованием метода сканирования. Принять величину интервала неопределенности [а, b] равной [0,10], а значение ε=0,2;

2. F(x)=x₁∙x₂+x₁²+2∙x₂²

найти значения переменных x₁ и x₂ при которых F(x) будет минимальна. Поиск оптимума осуществить с использованием поокоординатного спуска. Начальные координаты поиска x₁₀=2 и x₂₀=2, значение ε₁=0,2, ε₂=0,2.