Г. Нижний Новгород, 19 декабря 2004 года

Класс.

1. В пространстве расположены два единичных куба с общим центром. Доказать, что объем их пересечения больше ½.

Решение: Заметим, что вписанные в эти кубы шары совпадают (поскольку у них общий центр и равные радиусы). Тогда этот шар целиком находится внутри пересечения кубов, которое является некоторым выпуклым многогранником. Следовательно, объем пересечения кубов больше объема шара, равного .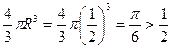

В некотором государстве 99 городов, некоторые пары городов соединены дорогами длиной в 1, 3 или 5 вёрст, причём от каждого города до каждого по этим дорогам можно добраться ровно одним способом. Из каждого города в каждый другой отправились гонцы с важным донесением. Докажите, что суммарное расстояние, пройденное гонцами, делится на 4.

Решение: Заметим, что каждая дорога делит все города на две части из N и (99–N) городов так, что путь из любого города первой части в любой город второй части проходит по ней. Но тогда эта дорога была учтена в нужной сумме 2N(99–N) раз, так как для каждой пары городов по ней прошли два гонца (туда и обратно). Но N и (99–N) – числа разной чётности, значит, 2N(99–N) делится на 4 и каждая дорога была учтена кратное 4 количество раз. Следовательно, и вся сумма делится на 4.

Комментарий: Как видим, в условии задачи нечётность длин дорог (1, 3 и 5) никакой роли не играет. Это просто избыточное условие, а факт верен при любых целочисленных длинах дорог.

3. Прямая, параллельная диагонали BD и проходящая через Y – точку пересечения диагоналей AC и BE правильного пятиугольника ABCDE, пересекает сторону AB в точке X. Найдите ÐBCX. (Ответ привести в градусах)

Y

D

В

Ответ: 18°. Решение (см.рис.5): XYïïBDïïAE , поэтому BX/XA=BY/YE=BC/CE (т.к. CY – биссектриса DВСЕ, что следует из равенства углов ÐBCA=ÐACE, опирающихся на равные дуги ВА и АЕ описанной около правильного пятиугольника окружности) = BC/CA (т.к. CE=CA), поэтому X – основание биссектрисы угла ÐС в DABC, отсюда ÐBCX=ÐВCА/2=ÐBCD/6=108°/6=18°.

4. Назовём натуральное число малым, если оно меньше числа-перевёртыша, получаемого из него перестановкой цифр в обратном порядке. Обозначим через М(n) количество малых n-значных чисел. Сколькими нулями оканчивается число М(n)?

Ответ: М(n) при n³4 оканчивается на [(n–3)/2] нулей, где [x] – целая часть числа x; М(1) и М(3) оканчиваются на 1 нуль; М(2) оканчивается на 0 нулей.

Решение: Рассмотрим сначала случай чётного n=2k. Из множества n-значных чисел, не оканчивающихся на 0 (а их всего 9×10^2k–2×9), уберём те, которые при переворачивании равны себе (их 9×10^k–1). Остальные числа разбиваются на пары n-значных перевёртышей, из которых одно число будет малым, а другое – немалым. Таким образом,

М(n)=(81×10^2k–2–9×10^k–1)/2 =9×10^k–1×(9×10^k–1–1)/2=45× (9×10^k–1–1) ×10^k–2. Но первые два множителя нечётны при k³2, значит, M(n) оканчивается на k–2=(n–4)/2 нуля.

В нечётном случае n=2k+1 при k³2 получим M(n)= 45× (9×10^k–1–1) ×10^k–1, т.е. M(n) оканчивается на k–1=(n–3)/2 нуля. Таким образом, количество нулей равно [(n–3)/2], где [x] – целая часть числа x.

Рассмотрев случаи маленьких n, получим, что M(1)= 0, М(2)=36, М(3)=360.

5. Сумма неотрицательных чисел a, b, c равна 3. Докажите неравенство a³b+b³c+c³a³3(ab+bc+ca-2).

Решение: Перенесём всё в одну сторону и с учётом условия a+b+c=3 получим:

a³b+b³c+c³a–3(ab+bc+ca-2) = a³b+b³c+c³a–3ab–3bc–3ca+2a+2b+2c =

= a(c³–3c+2)+ b(a³–3a+2)+c(b³–3b+2)= a(c–1)²(c+2)+b(a–1)²(a+2)+c(b–1)²(b+2)³0, что и требовалось доказать.

6. В правильном 2n–угольнике проведены стороны и главные диагонали. За ход (если возможно) отмечается вершина так, чтобы никакие две отмеченные вершины не были соединены отрезком. Мог ли процесс окончиться ровно после 2004 ходов?