Исполнительный механизм

Содержание

Цель работы.. 3

Задание на курсовую работу. 3

Математическая модель системы регулирования. 4

1.Вытяжной прибор. 4

2. Датчик. 4

3. Регулятор. 5

4. исполнительный механизм.. 6

Расчет. 6

Результаты.. 8

Программа. 8

Цель работы

Целью курсовой работы является развитие навыков статистического моделирования на ЭВМ систем автоматического регулирования (САР) технологических процессов. Работа предусматривает составление математических моделей САР и возмущающих воздействий, их преобразование в удобную для реализации на ЭВМ форму, разработка программы для ЭВМ и ее непосредственное использование с последующей обработкой и оценкой результатов моделирования.

Вариант29

Дано : 2000 120 0,02

Задание на курсовую работу

Система регулирования линейной плотности чесальной машины.

На рис.1 показана схема автоматизации процесса вытягивания ленты в вытяжном приборе чесальной машины.

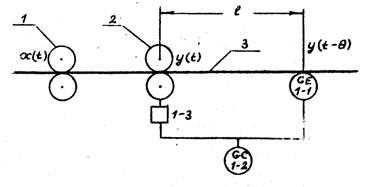
В процессе вытягивания пара выпускных роликов 1 вытяжного прибора вращается с постоянной частотой, обеспечивая постоянную линейную скорость V₁ м/с, ленты 3.Пара выпускных валиков 2 в номинальном режиме обеспечивает линейную скорость ленты V₂₀ м/c, чем создается вытяжка E=V₂₀/V₁.

Система регулирования предназначена для стабилизации линейной плотности y(t), ктекс, в случае отклонений режима работы от номинального. Основной причиной этих отклонений является изменение линейной плотности x(t) ктекс, ленты на выходе.

Система состоит из вытяжного прибора (объекта регулирования), датчика линейной плотности 1-1, регулятора 1-2 и исполнительного механизма 1-3. Датчик преобразует отклонения выходной линейной плотности от номинала в электрический сигнал, который подвергается дальнейшим преобразованиям в регуляторе и после усиления поступает на исполнительный механизм. Исполнительный механизм увеличивает частоту вращения валиков 2 и линейную скорость ленты на выходе при положительных, и уменьшает при отрицательных отклонениях линейной плотности от номинала.

Параметры системы регулирования(вариант 29)

T_p=6.0 c

m_x=5 кТекс

δ_x= 0,4 кТекс

α=0,25 c^-1

V₁=1 м/c

V₂₀=1,5/c

y₀=4 ктекс

K_д=1 В/ ктекс

K_p=400

T_и=0,5с

K_и=0,01м/Вc

Математическая модель системы регулирования

Рассмотрим уравнения элементов системы регулирования

Вытяжной прибор

Исходя из условия баланса массы чесальной ленты на входе и выходе в вытяжной прибор, получим 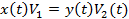(1)

Где 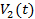- переменная линейная скорость ленты, обеспечиваемая выпускной парой валиков в процессе регулирования м/с.

В левой части уравнения – масса ленты, поступающей в вытяжной прибор, в правой – выходящей из него в единицу времени. Следует отметить, что это уравнение описывает процесс вытягивания лишь в самых общих чертах, игнорируя, в частности, возможные кратковременные «сгущения» и «разрежения» линейной плотности внутри вытяжного прибора, не учитывая волокнистую структуру прибора и т.п.

Преобразуя (1), запишем уравнение объекта (вытяжного прибора) в форме

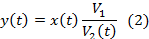
Отметим, что зависимость 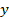от 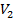– нелинейная.

Подставив значения получим:

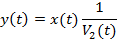
Датчик

Датчик линейной плотности представляет собой преобразователь текущего значения толщины проходящей через него ленты в электрический сигнал. В силу конструктивных особенностей чесальной машины датчик не может быть размещен непосредственно за вытяжным прибором и всегда располагается на некотором расстоянии l м, от него отчитываемом вдоль ленты.

Таким образом, если считать регулируемой величиной y(t), то датчик измеряет значение y(t-θ),

где θ – время прохождения ленты от выпускной пары валиков вытяжного прибора до датчика. Это время в процессе работы может несколько меняться вследствие изменения скорости V₂(t), составляя в среднем значение:

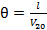(3)

В дальнейшем будем считать запаздывание датчика постоянным, равным 0,6 с

Датчик может быть построен в соответствии с различными принципами (фотоэлектрическим, емкостным и др.), но независимо то этого в системе его можно считать практически безынерционными ( по сравнению с другими элементами) звеном, описываемым линейным уравнением

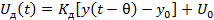(4)

Где 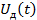- выходной сигнал датчика, В;

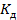- коэффициент усиления датчика, В/ ктекс

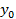- номинальное (заданное) значение линейной плотности на выходе вытяжного прибора, ктекс

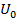– напряжение на выходе датчика при нормальной линейной плотности, В.

Подставим данные:

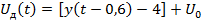
Регулятор

Регулятор построен по схеме, показанной на рис. 2. Он состоит из преобразователя на основе операционного усилителя 1 с резистором R и конденсатором С в цепи обратной связи и усилителя мощности 2.

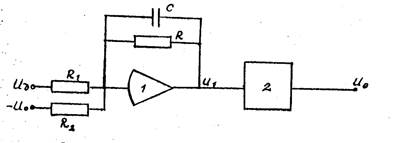
Рис. 2 . Схема регулятора

Преобразователь описывается уравнением:

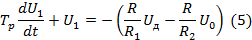
Где 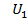- выходное напряжение операционного усилителя, В;

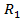и 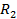- выходные сопротивления, МОм;

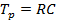– постоянная времени регулятора, с.

Постоянное напряжение 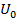вводится с тем, чтобы на входе операционного усилителя действовало напряжение, пропорциональное отклонению линейной плотности от номинального значения ,

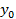При 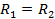получим

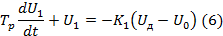
Таким образом, преобразователь является апериодическим звеном первого порядка с постоянной времени 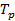и коэффициентом усиления 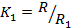, на выходе которого фигурирует сигнал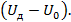

Преобразователь является самым инерционным звеном в системе, а усилитель мощности по сравнению с ним можно считать безынерционным звеном с коэффициентом усиления K₂

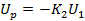(7)

Согласно 6 и 7 уравнение регулятора в целом имеет вид

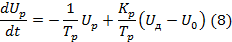
Где 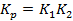– коэффициент усиления регулятора.

Подставив заданные значения получим:

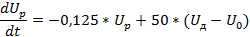
исполнительный механизм

В состав исполнительного механизма входят двигатель постоянного тока, на якорную обмотку которого подается сигнал 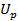, и дифференциал. Двигатель является апериодическим звеном первого порядка и описывается уравнением

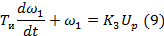
Где 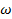₁-частота вращения ротора двигателя, с^-1;

T_и- постоянная времени двигателя ( и исполнительного механизма в целом), с;

K₃ – коэффициент усиления двигателя, 1/Вс.

Дифференциал представляет собой механическое устройство, в котором частота вращения выходного вала является суммой частот вращения двух его входных валов. Выходной вал приводит в движение выпускную пару валиков вытяжного прибора. Один из входных валов вращается с постоянной частотой от главного привода чесальной машины, несет основную нагрузку по перемещению ленты и обеспечивает ее линейную скорость V₂₀ на выходе вытяжного прибора. Второй вал вращается от двигателя с частотой ω₁, чем обеспечивается изменение линейной скорости ленты на выходе на величину K₄ ω_1, в которой коэффициент K_и, м, определяется диаметром ведущего валика выпускной пары и передаточными числами в цепи двигатель - валики.

Таким образом, линейная скорость ленты V₂(t) на выходе вытяжного прибора равна

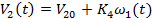(10)

Считая выходной координатой исполнительного механизма V₂, а входной – U_p, получим его уравнение на основе 9 и 10.

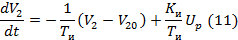
Где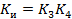

Подставим значения:

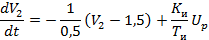
Расчет

Произведем расчет шага ∆t из двух условий:

1) 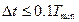, где Т_min – минимальный из временных параметров системы (постоянных времени, запаздывания и др.)

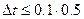
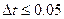
2)

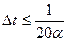
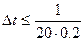
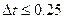
Исходя из двух условий выбрали ∆t=0.05

Выберем интервал регулирования t_м-t_п. При ограниченных возможностях пробного моделирования и для предварительного выбора интервала можно воспользоваться следующей рекомендацией: интервал (t_м-t_п)должен превосходить время корреляции процесса у₀ примерно в 30 раз (или более).

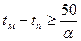
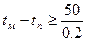
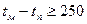
Следовательно время процесса 250с.

Расчетные формулы

Преобразуем уравнения:

1) линейной скорости ленты

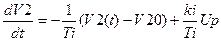
2) уравнение регулятора

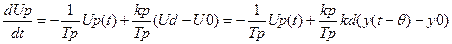
Следуя методу Эйлера, построим систему равноотстоящих на ∆t точек ti=i∆t

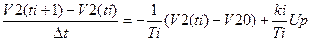
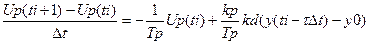
ϴ=τ∆t

Дальнейшие преобразования системы приводят к формулам, которые представляют собой по существу алгоритм вычисления V2, Up.

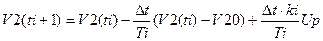
Результат

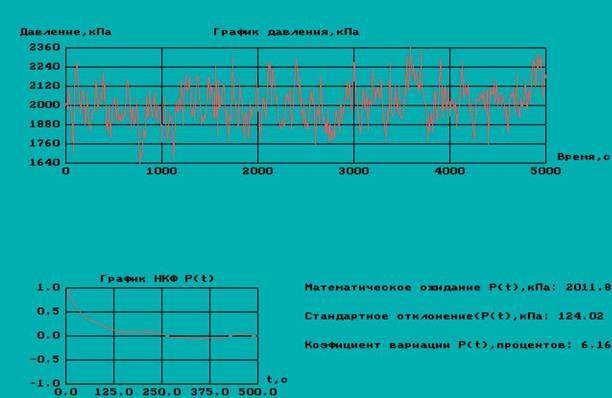
Программа

/*Курсавая работа по дисцеплине моделирование систем на тему:

"Моделирование случайного процессаизменения давления"

студент группы 4-мд-6 Шумакова Алексея.

Вариант 29 */

#include <stdio.h>

#include <math.h>

#include <stdlib.h>

#include <graphics.h>

#include <time.h>

#include <conio.h>

/* Обьявление переменных */

float P[5001];

float ksi,A,B,dt=2.5,alf=0.02,m=2000,sig=120,z;

float m_,D_,sig_,v_,NKF[201],sum;

int i,j,pp,L=200;

char ch[80];

main()

{

/*инициализация графического режима*/

int gdr=DETECT, gmod;

initgraph(&gdr, &gmod, " ");

/**********************************************/

/*Получение масива значения давления*/

randomize();

A=exp(-alf*dt);

B=sig*sqrt(1-A*A);

P[0]=0;

for(i=1; i<5001; i++){

z=0;

for(j=1; j<13; j++)

{

ksi=rand()/32767.0;

z=z+ksi;

}

z=z-6.0;

P[i]=A*P[i-1]+B*z;

}

for(i=0;i<5001;i++)

P[i]=P[i]+m;

/*********************************************************************/

/*График реализации процесса*/

/*Создание фона*/

setfillstyle (1,3);

bar (0,0,640,480);

/* нанесение сетки и надписи */

setcolor (0);

setlinestyle (0,0,1);

for (i=0;i<7;i++)

line (70,50+20*i,570,50+20*i);

for (i=0;i<6;i++)

line (70+100*i,50,70+100*i,170);

settextjustify (2,1);

for (i=0;i<7;i++)

{ sprintf(ch,"%d",2360-120*i);

outtextxy (65,50+20*i,ch);

}

settextjustify (1,2);

for (i=0;i<6;i++)

{ sprintf (ch,"%d",0+1000*i);

outtextxy (70+100*i,175,ch);

}

outtextxy (300,30,"График давления,кПа");

outtextxy (610,160,"Время,с");

outtextxy (70,30,"Давление,кПа");

/*построение графика*/

setcolor(12);

setlinestyle(0,0,1);

moveto (70,110);

for (i=1; i<501; i++)

{ pp=110-(P[i*10]-m)*20/120+0.5;

lineto (70+i,pp);

}

/*обработка результатов моделирования*/

m_=0;

for(i=0;i<5001;i++)

{ m_=P[i]+m_;

}

m_=m_/5001;

D_=0;

for(i=0;i<5001;i++)

{ D_=D_+((P[i]-m_)*(P[i]-m_));

}

D_=D_/5001;

sig_=sqrt(D_);

v_=sig_/m_*100;

/*Оценка нормараванной корреляционнойфункции*/

for(i=0;i<L+1;i++)

{sum=0;

for(j=0;j<5001-i;j++)

sum=sum+(P[j]-m_)*(P[j+i]-m_);

NKF[i]=sum/(5001-i)/D_;

}

/*Вывод числовых оценок*/

setcolor(0);

settextjustify(0,1);

sprintf(ch,"Математическое ожидание P(t),кПа: %.2f",m_);

outtextxy(320,300,ch);

sprintf(ch,"Стандартное отклонение<P(t),кПа: %.2f",sig_);

outtextxy(320,330,ch);

sprintf(ch,"Коэфициент вариации P(t),процентов: %.2f",v_);

outtextxy(320,360,ch);

getch();

} /*end*/