Решение типовой задачи МОБ

3-х отраслевая экономическая система задана матрицей коэффициентов прямых затрат А и вектором конечной продукции Y:

, .

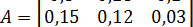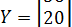Найти:

1) коэффициенты полных затрат: В = (b_ij) = (b₁, b₂, b₃);

2) плановые объемы валовой продукции: Х = (x_i) = (x₁, x₂, x₃);

3) величину межотраслевых потоков средств производства, т.е. значения x_ij, i=1, 2, 3; j = 1, 2, 3;

4) объемы условно-чистой продукции z_j;

5) матрицу косвенных затрат С =(с_ij) = B - A - E.

6) По заданному вектору увеличения выпуска конечной продукции ΔY=(Δy₁,Δy₂,Δy₃)=(20, 10, 5) определить изменение плана производства валовой продукции ΔX.

Результаты вычислений п.п. 1-4 представить в форме МОБ.

Решение

Используем уравнения МОБ

в развернутом виде: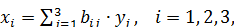

в матричном виде: X = (E - A)^-1 · Y = B Y.

1) Находим матрицу полных затрат В = (E - A)^-1:

E - A = ;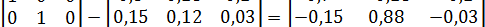

Обращаем матрицу E - A, т.е. найдем В = (E - A)^-1.

Вычисляем определитель Δ=|E - A|= 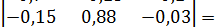0,511.

Так как Δ≠0, то существует матрица В = (E - A)^-1, обратная заданной матрице E-A.

Находим алгебраические дополнения для элементов матрицы K = E - A:

; ;

;

;

;

.

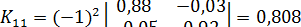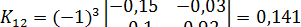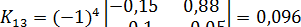
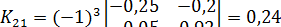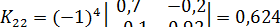
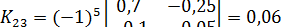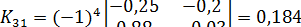
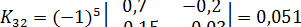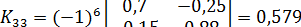Составляем матрицу из алгебраических дополнений:

.

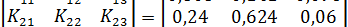Транспонируем эту матрицу (получим приведенную матрицу) и делим ее на определитель Δ=0,511; в результате получаем обратную матрицу В = (E - A)^-1:

В = (E - A)^-1 = .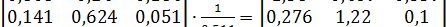

Таким образом, матрица коэффициентов полных затрат

В = (E - A)^-1 = .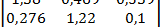

2) Находим объемы производства отраслей (валовая продукция):

X = B Y = .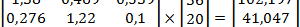

Следовательно, плановые объемы валовой продукции трех отраслей, необходимые для обеспечения заданного уровня конечной продукции, равны:

х₁=102,197; х₂=41,047; х₃=26,383.

3) Рассчитываем значения межотраслевых потоков x_ij=a_ij· x_j:

x₁₁=0,3·102,2=30,7; x₁₂=0,25·41,0=10,2; x₁₃=0,2·26,4=5,3;

x₂₁=0,15·102,2=15,3; x₂₂=0,12·41,0=4,9; x₂₃=0,03·26,4=0,8;

x₃₁=0,1·102,2=10,2; x₃₂=0,05·41,0=2,1; x₃₃=0,08·26,4=2,1.

4) Результаты вычислений представим в форме МОБ. Величина условно-чистой продукции z_j определяется как разница между валовой продукцией отрасли x_j и суммой межотраслевых потоков в каждом столбце:

.

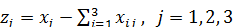Потребляющие отрасли (j)   Производящие отрасли (i)				Конечный продукт yi	Валовой продукт xi
	30,7	10,2	5,3		102,2
	15,3	4,9	0,8		41,0
	10,2	2,1	2,1		26,4
Условно-чистый продукт zj	46,0	23,8	18,2
Валовой продукт xj	102,2	41,0	26,4		169,6

Таким образом, на основе заданных матриц по уровню конечного продукта Y и коэффициентов прямых затрат A получен полностью сбалансированный план общего производства продукции и ее распределения в качестве средств производства между отраслями и в качестве продукции для конечного использования.

5) Найдем матрицу косвенных затрат по формуле: С = (с_ij) = B - A - E = =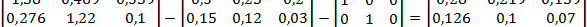

6) Определяем изменение плана ΔX, которое потребуется при увеличении выпуска конечной продукции 1-й отрасли на 20 ед., 2-й – на 10 ед. и 3-й – на 5 ед.

ΔX = B ΔY =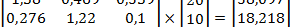

Следовательно, потребуется увеличить выпуск валовой продукции 1-й отрасли на Δx₁=38,1 ед., 2-й отрасли – на Δx₂=18,2 ед., 3-й отрасли – на 10,6 ед.