Транспортная задача по критерию времени

Задача по критерию времени возникает при перевозке срочных грузов. Как и в обычной транспортной задаче, имеется m поставщиков с запасами однородного груза в количестве а_1, а₂, …, а_m и n потребителей, которым этот груз должен быть доставлен в объеме b₁, b₂, …, b_n. Известно t_ij, i=1, 2, …, m, j=1, 2, …, n – время, за которое груз доставляется от каждого i-го поставщика каждому j-му потребителю. Требуется составить такой план перевозок груза, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью и наибольшее время доставки всех грузов является минимальным.

Составим математическую модель этой задачи. Обозначим x_ij – объем перевозимого груза от i-го поставщика j-му потребителю. Система ограничений задачи не отличается от системы ограничений обычной транспортной задачи. Пусть X=(x_ij), i=1, 2, …, m, j=1, 2, …, n – некоторое опорное решение задачи. Запишем целевую функцию задачи. Обозначим через T(X) наибольшее значение элементов матрицы T=(t_ij), i=1, 2, …, m, j=1, 2, …, n, соответствующих клеткам таблицы, занятым опорным решением: T(X)= 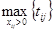. Таким образом, за время T(X) план перевозок будет выполнен полностью. Математическая модель имеет вид:

T(X)= 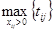→min, (5.4.1.)

, i=1, 2, …, m, (5.4.2)

, j=1, 2, …, n, (5.4. 3.)

x_ij≥0, i=1, 2, …, m, j=1, 2, …, n. (5.4.4.)

Задача решается в следующем порядке. Находится начальное опорное решение X₁. Определяется значение целевой функции T(X₁)= 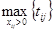= 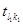. Все свободные клетки, которым соответствуют значения t_ij>T(X₁), исключаются из рассмотрения (перечеркиваются). Занимать эти клетки нецелесообразно, так как повысится значение целевой функции. Чтобы понизить ее значение, необходимо освободить клетку (l₁, k₁), в которой t_ij достигает максимума. Для этого строят так называемые разгрузочные циклы, которые могут включать в свой состав несколько свободных клеток. В каждом разгрузочном цикле, начиная с разгружаемой клетки (l₁, k₁), расставляются поочередно знаки «—» и «+» и осуществляется сдвиг на величину 0=max{x_ij}. Если удается эту клетку разгрузить, то она исключается из рассмотрения (зачеркивается). Получается новое опорное решение X₂, на котором значение целевой функции меньше, чем на X₁. Далее снова пытаются разгрузить клетку, соответствующую T(X₂)= 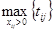= . Процесс продолжается до тех пор, пока возможность разгрузить соответствующую клетку не исчезнет.

Пример. Найти минимальное время на осуществление всех перевозок для задачи, исходные данные которой приведены в табл. 5.4.1.

Таблица 5.4.1

bj ai
		8 - 30		+
		+		- 10

Таблица 5.4.2

bj ai
	10 - 20	+
	+	20 -

Р е ш е н и е. Составим начальное опорное решение X₁ по методу северо-западного угла (см. табл. 5.4.1). Базисные нули не записываем. Максимум целевой функции T(X₁)= =12 достигается в клетке (3, 4). Перечеркнем клетку (4, 1), в которой время доставки груза t₄₁= 15 больше T(X₁)=12.

Для улучшения решения разгрузим клетку (3, 4) с помощью цикла (3, 4), (2, 4), (2, 2), (3, 2). Обозначим цикл, найдем 0=min{10, 30}=10. Осуществив сдвиг по циклу, получим второе опорное решение X₂ (табл. 5.4.2). Максимум целевой функции на этом опорном решении T(X₂)= 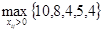=10 достигается в клетке (1, 1). Перечеркнем клетку (3, 4), так как время t₃₄=12 больше, чем T(X₂)=10. Разгрузим клетку (1, 1) с помощью цикла (1, 1), (1, 2), (2, 2), (2, 1). Означим цикл, найдем 0=min{20, 20}=20. Осуществив сдвиг по циклу, получим третье опорное решение X₃ (табл. 5.4.3)

Таблица 5.4.3

bj ai
		20 -	+
		+ 4	- 5

Таблица 5.4.4

bj ai

Максимум целевой функции на этом опорном решении T(X₃)= {6,5,4,4,5,4,}=6 и достигается в клетке (1, 2). Перечеркнем клетки (1, 1), (2, 2), (2, 3) и (4, 3): в них время t₁₁=10, t₂₂=8, t₂₃=7 и t₄₃=9 больше, чем T(X₃)=6. Разгрузим клетку (1, 2) с помощью цикла (1, 2), (1, 3), (3, 3), (3, 2). Означим цикл, найдем 0=min {20,20}=20. Осуществив сдвиг по циклу, получим четвертое опорное решение X₄ (табл. 5.4.4). Максимум целевой функции на этом опорном решении T(X₄)= { 5,4,4,5,4,}=5 и достигается в клетках (2, 1) и (3, 3). Перечеркнем клетки (1, 2) и (4, 2), в которых время перевозок не менее t₂₁=5. С помощью оставшихся невычеркнутых клеток разгрузить клетки (2, 1) и (3, 3) не удается, поэтому X₄ является оптимальным решением.

Ответ: min T(X)=5 при X*= •

СПИСОК ЛИТЕРАТУРЫ.

1. Ермаков В.И. Общий курс высшей математики для экономистов: Учебник для экон. спец. вузов / Под ред. В.И. Ермакова. М.: ИНФРА-М., 1999.656 с.

2. Зайцев М.В. Прикладная математика: Сборник задач. Ч. 1. / М.В. Зайцев, А.А. Беляев. М.: Изд-во МГУК., 1999. 32 с.

3. Зайцев М.В. Прикладная математика: Сборник задач. Ч. 2. / М.В. Зайцев, А.А. Беляев. М.: Изд-во МГУК., 1999. 39 с.

4. Плотникова С.В. Математика в экономике: Метод. разработки и контр. задания / С.В. Плотникова. Тамбов: Изд-во Тамб. гос. техн. Ун-та, 1997. 52 с.

5. Матвеев В.И. Курс линейного программирования: Учеб. пособие / В.И. Матвеев, Р.В. Сачитов, В.Г. Шершнев. М: Изд-во «Менеджер», 1998. 102 с.