МКЭ для задачи Неймана
Приближенным решением задачи (3.6), (3.7) назовем функцию 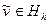 , удовлетворяющую уравнению
, удовлетворяющую уравнению
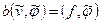 (3.17)
(3.17)
при произвольной функции 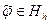 .
.
Система уравнений для определения неизвестных 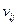 в этом случае имеет вид
в этом случае имеет вид
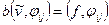 ,
, 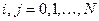 . (3.18)
. (3.18)
Число сеточных уравнений в системе (3.18) равно числу всех узлов сетки в 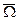 .
.
Заметим, что в силу естественности краевого условия (3.7), на функцию 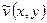 никаких дополнительных ограничений на границе области не накладывается.
никаких дополнительных ограничений на границе области не накладывается.
Не останавливаясь подробно на вычислениях и используя явные представления 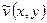 и
и 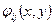 , выпишем результат. Во внутреннем узле сетки уравнения имеют вид
, выпишем результат. Во внутреннем узле сетки уравнения имеют вид
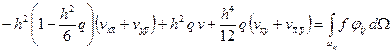 . (3.19)
. (3.19)
В отличие от уравнения Пуассона схема для уравнения (3.6) уже не пятиточечная, а семиточечная, что связано с наличием в уравнении дополнительного члена. Очевидно, что усложнение уравнения далее не приведет к расширению шаблона, так как каждая координатная функция не ортогональна не более чем шести другим координатным функциям.
Выпишем уравнение, соответствующее одному из граничных узлов, например, узлу 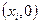 (рис.14):
(рис.14):

Рис.14. Область 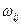 для граничного узла
для граничного узла
Это уравнение имеет вид
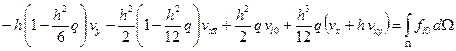 . (3.20)
. (3.20)
То, что уравнение (3.19) аппроксимирует уравнение (3.6), следует из вида сеточного уравнения, а то, что (3.20) аппроксимирует граничное условие (3.7), следует пояснить.
Предположим, что 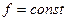 . Тогда уравнене (3.20) перепишется так:
. Тогда уравнене (3.20) перепишется так:
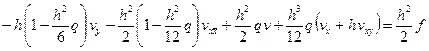 . (3.21)
. (3.21)
Решение 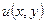 удовлетворяет краевому условию (3.7), т.е.
удовлетворяет краевому условию (3.7), т.е.
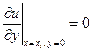 .
.
Используя формулу Тейлора
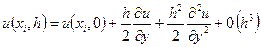 ,
,
с учетом уравнения (3.6) получим соотношение
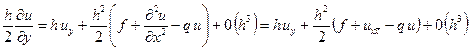 .
.
Отсюда следует, что граничное условие (3.7) можно приблизить равенством
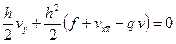 . (3.22)
. (3.22)
Сопоставление (3.21) и (3.22) показывает, что (3.21) также аппроксимирует граничное условие (3.7).
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ.. 1
1. ДВУХТОЧЕЧНАЯ КРАЕВАЯ ЗАДАЧА.. 4
1.1. Постановка задачи. Различные формулировки. 4
1.2. Задача с разрывными коэффициентами. 7
1.3. Методы Галеркина и Ритца. 8
1.4. Метод сеток. Составление сеточных уравнений. 10
1.5. Метод конечных элементов. 11
1.6. Составление системы сеточных уравнений МКЭ.. 13
1.7. МКЭ – вторая краевая задача. 14
1.8. Матричная запись систем сеточных уравнений МКЭ.. 15
1.9. Разрешимость системы сеточных уравнений МКЭ.. 17
1.10. МКЭ для уравнений 4-го порядка. 18
1.11. О выборе координатных функций МКЭ.. 20
1.12. МКЭ – инженерный подход. 21
1.13. Сходимость МКЭ.. 26
1.14. Оценки аппроксимации. 28
1.15. Метод сеток. Исследование разрешимости и сходимости. 29
1.16. Метод сеток. Метод энергетических оценок. 31
1.17. О точности оценок погрешности. 34
2. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ. МЕТОД СЕТОК 35
2.1. Об уравнениях в частных производных. 35
2.2. Метод сеток для стационарных задач. 37
2.3. Аппроксимация стационарных задач. Общие формулировки. 38
2.4. О корректности сеточных задач. 40
2.5. Аппроксимация нестационарных задач. 41
2.6. Счетная устойчивость разностных схем.. 45
2.7. Методы решения нестационарных задач. 48
3. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ. МКЭ 50
3.1. Уравнение Пуассона в прямоугольнике. 50
3.2. Кусочно-линейные координатные функции. 52
3.3. МКЭ для задачи Дирихле. 54
3.4. МКЭ для задачи Неймана. 55
