Решение типовых задач I тура прошлых лет
I вариант
(8 класс 1998 г.)
1. Решить неравенство: 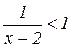
Решение: 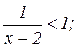
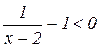
Приводим левую часть к общему знаменателю: 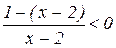 ;
; 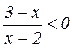
Дробь отрицательна, если числитель и знаменатель имеют разные знаки:
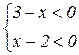 или
или 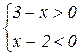 Þ
Þ 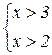 или
или 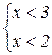
2. Построить график функции: 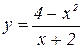
 Решение: Область определения функции – все значения х, кроме
Решение: Область определения функции – все значения х, кроме 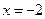 , далее при
, далее при 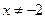 имеем
имеем 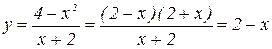 ; итак, при
; итак, при 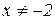
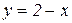
Графиком функции 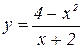 является прямая с выколотой точкой, абсцисса которой равна -2.
является прямая с выколотой точкой, абсцисса которой равна -2.
3. Увеличится или уменьшится правильная положительная дробь a/b, где a>0, b>0, если к числителю и знаменателю прибавить одно и тоже положительное число d?
Решение: Рассмотрим разность
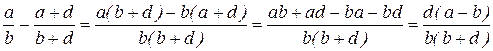
Поскольку 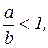 то d(a-b)<0, b(b+d)>0 , ( d >0, a-b<0, b>0).
то d(a-b)<0, b(b+d)>0 , ( d >0, a-b<0, b>0).
Итак, 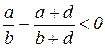 , т.е.
, т.е. 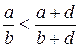 .
.
4.  Дан треугольник АВС, Н - точка пересечения его высот. ВН=АС. Найдите угол АВС.
Дан треугольник АВС, Н - точка пересечения его высот. ВН=АС. Найдите угол АВС.
Решение: 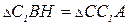 , по гипотенузе
, по гипотенузе 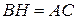 и острому углу:
и острому углу: 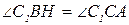 ;
; 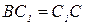 ;
; 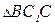 - равнобедренный, прямоугольный
- равнобедренный, прямоугольный 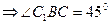 . Если
. Если 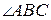 - острый (рис.1), то
- острый (рис.1), то 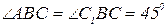 , если
, если 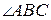 - тупой (рис.2), то
- тупой (рис.2), то 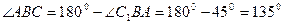
5. Можно ли любой остроугольный треугольник, не имеющий равных сторон, рассечь прямой, проходящей через вершину, на 2 подобных треугольника?
Решение: Пусть L секущая прямая. Если L не перпендикулярна стороне треугольника, то из образовавшихся двух треугольников один является остроугольным, а второй тупоугольным, поэтому они не являются подобными. Если L перпендикулярна стороне треугольника, то если полученные прямоугольные треугольники подобны, то два острых угла, прилежащих к общей стороне, составляют в сумме 90°, что противоречит условию задачи.
I вариант
(8 класс, 2002 г.)
1. Катер проплыл 15 км вниз по течению реки за 1 час и вернулся обратно за 1,5 часа. Найти скорость катера в стоячей воде и скорость течения реки.
Решение: Пусть x км/ч – скорость катера в стоячей воде, y км/ч – скорость течения реки. Тогда скорость по течению – (x+y) км/ч, скорость против течения – (x-y) км/ч. Используя условие задачи составляем систему уравнений: 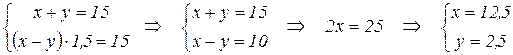
Ответ: скорость катера в стоячей воде 12,5 км/ч; скорость течения реки 2,5 км/ч.
2. Площадь прямоугольного треугольника 150, один из катетов равен 15. Найти длину высоты, опущенной из вершины прямого угла.
Решение:
 Дано: ∆АВС – прямоугольный (угол С=90˚); СВ=15;
Дано: ∆АВС – прямоугольный (угол С=90˚); СВ=15; 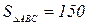 ;
; 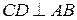
Найти: CD
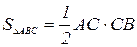 ,
, 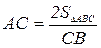 ; АС=20.
; АС=20.
По теореме Пифагора: 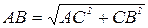 ; АВ=25
; АВ=25
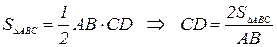 ; CD=12
; CD=12
Ответ: CD = 12.
3. Медиана, проведённая к одной из боковых сторон равнобедренного треугольника, делит его периметр на части длиной 15 и 6. Найти длину боковой стороны.
Решение:
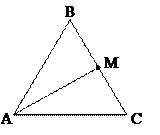 Дано: ∆АВС – равнобедренный (АВ=ВС); ВМ=МС;
Дано: ∆АВС – равнобедренный (АВ=ВС); ВМ=МС;
МС+АС = 6; АВ + ВМ = 15
Найти: ВС
Пусть МС=x; АС=y, тогда АВ=ВС=2x. 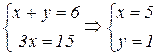
АВ=10
Ответ: АВ = 10
Замечание. Если предположить, что МС+АС=15, а АВ+ВМ=6, то получим АВ+ВС=8, АС=13, т.е. АВ+ВС<АС (ΔАВС не существует)
4. Если все стороны квадрата увеличить в два раза, то на сколько процентов увеличится его площадь?
Решение:
Пусть сторона старого квадрата – x, тогда сторона нового квадрата – 2x. Площадь старого квадрата: 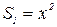 , площадь нового квадрата:
, площадь нового квадрата: 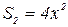 . Увеличение площади:
. Увеличение площади: 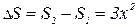 . Найдём сколько процентов число
. Найдём сколько процентов число 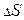 составляет от числа
составляет от числа 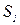 :
: 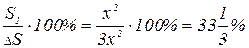 .
.
Ответ: площадь увеличится на 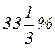 .
.
5. Один из корней уравнения 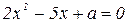 равен 1. Найдите другой корень.
равен 1. Найдите другой корень.
Решение: Т.к. 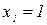 , то
, то 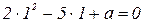 , отсюда
, отсюда 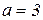
Найдём корни уравнения: 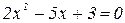 Þ
Þ 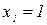 ;
; 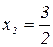
Ответ: 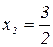 .
.
I вариант
(8 класс, 2004г.)
1. В равнобедренном треугольнике АВС АВ=ВС; АК – медиана; АК=6;  КАС=30○. Найдите стороны треугольника.
КАС=30○. Найдите стороны треугольника.
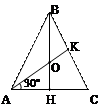 Решение: 1) Пусть ВН – высота в ΔАВС; ВН – медиана; ВН и АК пересекаются в т.О.
Решение: 1) Пусть ВН – высота в ΔАВС; ВН – медиана; ВН и АК пересекаются в т.О. 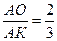 , АО = 4.
, АО = 4.
2) 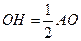 (катет, лежащий против угла в 30˚ в прямоугольном ΔАОН). ОН=2;
(катет, лежащий против угла в 30˚ в прямоугольном ΔАОН). ОН=2; 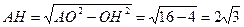 ;
;
3) 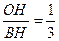 ;
; 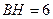 ; 4)
; 4) 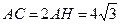 ;
; 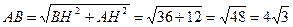 ;
;
5) 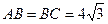 . Итак, все стороны ΔАВС равны, т.е. ΔАВС – равносторонний.
. Итак, все стороны ΔАВС равны, т.е. ΔАВС – равносторонний.
Ответ: 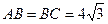
2. Решите уравнение: 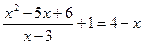 .
.
Решение: 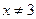 ;
; 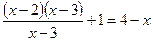 ;
; 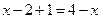 ;
; 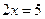 ;
; 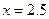
3. Найдите корни уравнения, зная, что они являются противоположными числами: 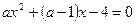 .
.
Решение: Т.к. имеются два различных корня, то 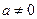 и
и 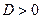 .
. 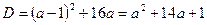 .
.
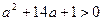 ,
, 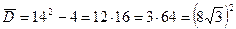
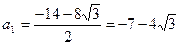 ;
; 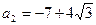
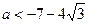 или
или 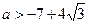
Т.к. 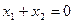 , то по теореме Виета
, то по теореме Виета 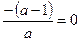 ;
; 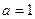
Уравнение 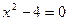 ;
; 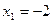 ;
; 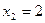
Ответ: 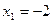 ;
; 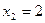
4. Найдите целые решения неравенства: 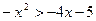 .
.
 Решение:
Решение: 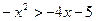 ;
; 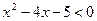 ;
; 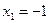 ;
; 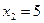
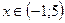
Ответ: 0; 1; 2; 3; 4.
5. Фермер собрал с двух участков 460 т клевера. На второй год на первом участке урожай увеличился на 15%, а на втором – на 10%, и общий урожай клевера составил 516 т. Сколько тонн клевера было собрано с каждого участка в первый год?
Решение: Пусть с I участка в 1-й год собрано x т, тогда со II участка в 1-й год (460-x)т. На второй год на I участке – 1,15x т, на II участке – 1,1(460-x)т.
1,15x+1,1(460-x)=516
1,15x+506-1,1x=516
0,05x=10; x=200
Ответ: с I участка в 1-й год собрано 200т, со II участка – 260т.
II вариант
(8 класс, 2004г.)
1. В прямоугольном треугольнике АВС известны углы  АВС=30○ и
АВС=30○ и  АСВ=90○. Точка D разбивает гипотенузу на части в 2см и 4см. Найдите длину отрезка СD.
АСВ=90○. Точка D разбивает гипотенузу на части в 2см и 4см. Найдите длину отрезка СD.
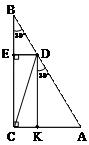 Решение: Пусть BD = 2; DA = 4. Проведём DE ^ ВС и DK ^ АС.
Решение: Пусть BD = 2; DA = 4. Проведём DE ^ ВС и DK ^ АС.
ΔBDE 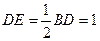 ; DE=CK=1;
; DE=CK=1;
ΔKDA 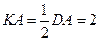 ;
; 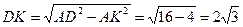 .
.
ΔCDK 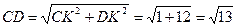
Ответ: 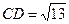 .
.
2. Решите уравнение: 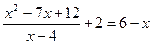 .
.
Решение: 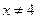 ;
; 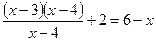 ;
; 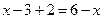 ;
; 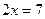 ;
; 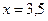 .
.
3. Найдите корни уравнения, зная, что они являются противоположными числами: 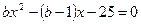 .
.
Решение: Т.к. уравнение имеет два различных корня, то 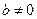 и
и 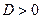 ;
; 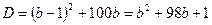
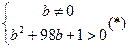 Т.к. x1+x2=0, то
Т.к. x1+x2=0, то 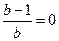 ;
; 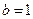 (условия (*)) выполняются.
(условия (*)) выполняются.
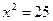 ;
; 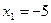 ;
; 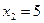
4. Найдите целые решения неравенства: 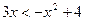 .
.
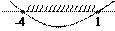 Решение.
Решение. 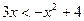 ;
; 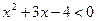 ;
; 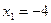 ;
; 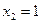
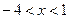
Ответ: 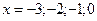 .
.
5. В январе два цеха изготовили 1080 деталей. В феврале первый цех увеличил выпуск деталей на 15%, а второй увеличил выпуск деталей на 12%, поэтому оба цеха изготовили 1224 детали. Сколько деталей изготовил в январе каждый цех?
Решение: Пусть в январе I цех изготовил x деталей, тогда II цех изготовил в январе (1080-x) деталей.
1,15x+1,12(1080-x)=1224
1,15x+1209,6-1,12x=1224
0,03x=14,4
x=480
Ответ: I цех в январе изготовил 480 деталей, а II цех – 600 деталей.
II вариант
(9 класс, 1998г.)
1. Сократить дробь: 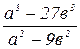
Решение: 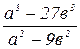 =
= 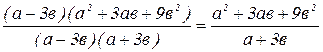
2. Катер прошёл 12 км против течения реки и 5 км по течению реки за то же время, которое ему понадобилось для прохождения 18 км по озеру. Какова собственная скорость катера, если известно, что скорость течения реки 3 км/час.
Решение: Пусть х км/час – собственная скорость катера. Тогда (х+3) км/час – скорость катера по течению реки, (х-3) км/час – скорость катера против течения реки. Общее время, затраченное катером на путь по реке - 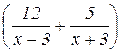 час. Время на путь по озеру -
час. Время на путь по озеру - 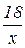 час. По условию задачи время по реке, затраченное на путь, и время по озеру, затраченное на путь, – одинаковое. Можно составить уравнение:
час. По условию задачи время по реке, затраченное на путь, и время по озеру, затраченное на путь, – одинаковое. Можно составить уравнение: 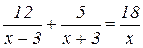 , решаем это уравнение:
, решаем это уравнение:
12 х (х+3) + 5 х (х-3) = 18 (х-3) (х+3)
х2 – 21 х - 162 = 0
х1 = -6, х2 = 27
х1 = -6 не подходит по смыслу задачи.
Ответ: 27 км/час.
1. Дана функция 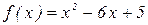 .
.
а) построить график функции 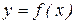 ; б) решить уравнение
; б) решить уравнение 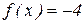 ;
;
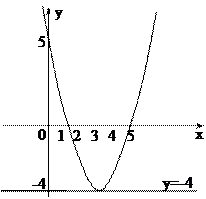 в) решить неравенство
в) решить неравенство 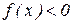 ;
;
г) при каких а уравнение 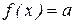 не имеет корней.
не имеет корней.
а) построить график функции 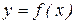
Решение:
Графиком функции у=х2-6х+5 является парабола. Точка пересечения с осью ОУ: х=0, у(0)=5. Точка пересечения с осью ОХ: у=0, х2-6х+5=0; х1=1, х2=5.
Прямая х=3 – ось симметрии параболы; х0=3 – абсцисса вершины параболы;
График функции у=f(х) изображен на рисунке:
Задачи б), в), г) можно решать обычным образом как квадратное уравнение, квадратное неравенство и уравнение с параметром. Но удобнее решать эти задачи графически, используя уже построенный график.
б) решить уравнение 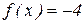
Решение: Решением этого уравнения будут абсциссы точек пересечения параболы у=f(х) и прямой у=-4.
Единственная точка пересечения этих линий – точка А(3;-4). Значит, уравнение имеет единственное решение х=3.
Ответ: х=3
в) решить неравенство 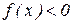
Решение:
Решением этого неравенства будут абсциссы точек параболы, лежащих ниже прямой у=0, т.е. ниже оси ОХ
Ответ: 1<x<5
г) при каких а уравнение 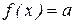 не имеет корней
не имеет корней
Решение:
Рассмотрим семейство прямых у=а. Эти все прямые параллельны оси ОХ. Уравнение f(х)=а не имеет корней, если прямая у=а не пересекает параболу у=х2-6х+5. Это будет для всех а<-4.
Ответ: а<-4
4. Меньшая сторона прямоугольника равна а, угол между диагоналями равен 120°. Найти радиус описанной окружности.
Решение:
 По условию задачи АВ=а
По условию задачи АВ=а 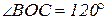 . Точка О – точка пересечения диагоналей является центром окружности описанной около прямоугольника, т.к. по свойству прямоугольника ОВ=ОС=ОD=ОА. ОВ – радиус описанной окружности.
. Точка О – точка пересечения диагоналей является центром окружности описанной около прямоугольника, т.к. по свойству прямоугольника ОВ=ОС=ОD=ОА. ОВ – радиус описанной окружности.
Рассмотрим 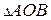 . Он равнобедренный, т.к. ОВ=ОА. Кроме того,
. Он равнобедренный, т.к. ОВ=ОА. Кроме того, 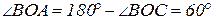 . Поэтому
. Поэтому 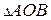 – равносторонний. ОВ=АВ=а.
– равносторонний. ОВ=АВ=а.
Ответ: R=а
I вариант
(9 класс, 2002г.)
1. Найдите наименьшее целое решение неравенства 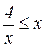 .
.
Решение: 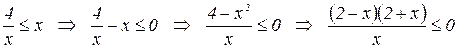
Найдём значения неизвестного, обращающие числитель и знаменатель в 0. Имеем 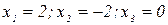 . Применим метод интервалов:
. Применим метод интервалов:
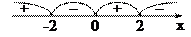 Применив метод интервалов, установим, что решением неравенства являются все
Применив метод интервалов, установим, что решением неравенства являются все 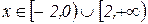
Ответ: Наименьшее целое решение неравенства 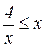 :
: 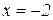 .
.
2. При каких а парабола 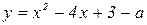 пересекает ось Ox в двух точках, расположенных по разные стороны от начала системы координат?
пересекает ось Ox в двух точках, расположенных по разные стороны от начала системы координат?
Решение:
Т.к. коэффициент при x2 равен 1>0, то ветви параболы направлены вверх. Парабола пересекает ось Оx в двух точках, значит, D>0. Наконец, эти точки расположены по разные стороны от начала системы координат, значит, 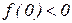 .
.
 Итак,
Итак, 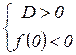
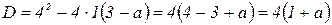
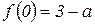
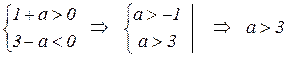
Ответ: 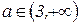
3. Товарный поезд был задержан в пути на 12 минут, а затем на расстоянии 60 км наверстал потерянное время, увеличив скорость на 15 км/час. Найти первоначальную скорость поезда.
Решение:
Пусть первоначальная скорость поезда x км/ч. На путь в 60 км потребовалось бы 60/x ч времени. Из-за задержки в пути скорость поезда увеличена на 15 км/ч, т.е. в действительности поезд шёл со скоростью (x+15) км/ч и на путь в 60 км потратил 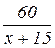 ч времени, что позволило наверстать потерянное в пути время в 12 мин.
ч времени, что позволило наверстать потерянное в пути время в 12 мин. 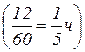 . Итак,
. Итак, 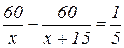 .
.
Решим уравнение: 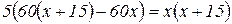
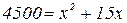
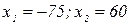
Отрицательное значение x не подходит по условию задачи.
Ответ: 60 км/ч
4. В прямоугольной трапеции основания равны 6 и 4. Диагональ равна 5. Найти периметр и площадь трапеции.
Решение:
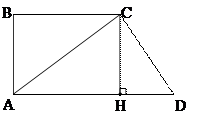 Так как по условию задачи ВС = 4; АD = 6, то диагональ АС = 5. Из ΔАВС имеем АВ2 = АС2-ВС2 = 25-16 = 9.
Так как по условию задачи ВС = 4; АD = 6, то диагональ АС = 5. Из ΔАВС имеем АВ2 = АС2-ВС2 = 25-16 = 9.
Итак, высота трапеции АВ = 3;
площадь 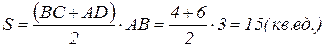
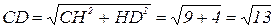 , т.к.
, т.к.
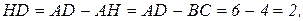
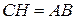
Периметр: 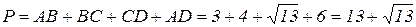
Ответ: 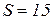 ;
; 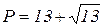
5. Найдите диаметр окружности, если его концы удалены от некоторой прямой, касающейся данной окружности, на 20 и 14.
Решение:
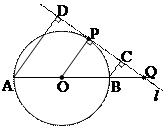 Пусть прямая l касается окружности в точке P и АВ – диаметр, AD = 20; ВС = 14. Рассмотрим ADCB; (
Пусть прямая l касается окружности в точке P и АВ – диаметр, AD = 20; ВС = 14. Рассмотрим ADCB; ( 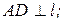
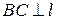 ) Þ ADCB - прямоугольная трапеция;
) Þ ADCB - прямоугольная трапеция; 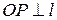 - радиус, проведённый в точку касания l с окружностью. Поскольку
- радиус, проведённый в точку касания l с окружностью. Поскольку 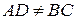 , то прямая АВ пересекает l в точке Q. Рассмотрим угол AQD. Стороны угла пересечены рядом параллельных прямых AD, OP, CB и АО = ОВ.
, то прямая АВ пересекает l в точке Q. Рассмотрим угол AQD. Стороны угла пересечены рядом параллельных прямых AD, OP, CB и АО = ОВ.
По теореме Фалеса DP = PC. Итак, OP – средняя линия трапеции ABCD. 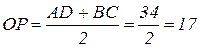 - радиус окружности. Диаметр окружности равен 34.
- радиус окружности. Диаметр окружности равен 34.
Ответ: 34.
I вариант
(9 класс, 2004г.)
1.  На катетах прямоугольного треугольника АВС вне его построены два квадрата АВDЕ и АСНК. Из точек D и Н на продолжение гипотенузы опущены два перпендикуляра HM и DN. Доказать, что сумма перпендикуляров HM и DN равна гипотенузе.
На катетах прямоугольного треугольника АВС вне его построены два квадрата АВDЕ и АСНК. Из точек D и Н на продолжение гипотенузы опущены два перпендикуляра HM и DN. Доказать, что сумма перпендикуляров HM и DN равна гипотенузе.
Решение: Из точки А проведём АР^СВ. ∆САР=∆НМС по острому углу и гипотенузе (  МНС=
МНС=  АСР, СН=СА). ∆АРВ=∆BDN (
АСР, СН=СА). ∆АРВ=∆BDN (  РАВ=
РАВ=  NBD, АВ=BD). НМ=СР, РВ=DN, отсюда HM+DN=BC.
NBD, АВ=BD). НМ=СР, РВ=DN, отсюда HM+DN=BC.
2. Пусть в равнобедренном треугольнике АВС биссектрисы равных углов А и С пересекают противоположные стороны соответственно в точках E и F. Доказать, что AFEC есть трапеция с тремя равными сторонами.
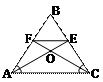 Решение: В треугольнике АВС АЕ и CF – биссектрисы =>
Решение: В треугольнике АВС АЕ и CF – биссектрисы =>  FAE=
FAE=  EAC=
EAC=  FCE=
FCE=  FCA.
FCA.
1) Рассмотрим ∆АОС – равнобедренный =>АО=ОС.
2) ∆FOC=∆ЕОС (по второму признаку) => AF=EC (1) и FO=OE.
3) В ∆FOE выполняется FO=OE, т.е.  EFO=
EFO=  FEO.
FEO.
4) В равнобедренных треугольниках FOE и АОС углы при вершине О равны =>равны и все остальные углы, т.е.  FEA=
FEA=  EAC. По признаку параллельности прямых (
EAC. По признаку параллельности прямых (  FEA=
FEA=  EАC – внутренние накрест лежащие углы при прямых EF и АС и секущей АЕ) прямые АС и FE – параллельны.
EАC – внутренние накрест лежащие углы при прямых EF и АС и секущей АЕ) прямые АС и FE – параллельны.
5) Наконец в ∆AFE  FAE =
FAE =  FEA, т.е. треугольник равнобедренный: AF=EF и (учитывая (1)) AF=EF=EC.
FEA, т.е. треугольник равнобедренный: AF=EF и (учитывая (1)) AF=EF=EC.
3. Найдите корни уравнения, зная, что они являются противоположными числами: 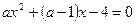 .
.
Решение: Т.к. имеются два различных корня, то 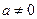 и
и 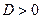 .
. 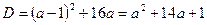 .
.
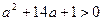 ,
, 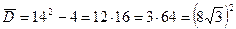
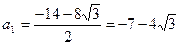 ;
; 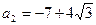
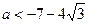 или
или 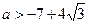
Т.к. 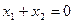 , то по теореме Виета
, то по теореме Виета 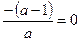 ;
; 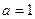
Уравнение 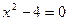 ;
; 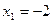 ;
; 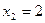
Ответ: 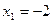 ;
; 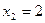
4. Найдите наибольшее целое решение неравенства: 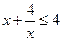 .
.
Решение: 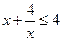 ;
; 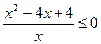 ;
; 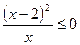
1) 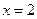 ;
; 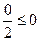 истинно
истинно
2) 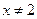 ,
, 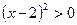 , тогда
, тогда 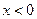 .
.
Ответ: 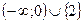 .
.
5. В двух баках содержалось 140л воды. Когда из первого бака взяли 26л воды, а из второго – 60л, то в первом баке осталось в два раза больше воды, чем во втором. Сколько литров воды было в каждом баке первоначально?
Решение: Пусть x л воды было в первом баке. Тогда (140-x) л воды было во втором баке. (x-26) л воды стало в первом баке (140-x-60) л стало во втором баке.
(80-x)·2=x-26
160-2x=x-26; 3x=186; x=62.
Ответ: в первом баке – 62л, во втором – 78л
II вариант
(9 класс, 2004г.)
1. В прямоугольном треугольнике АВС на гипотенузе АВ взяты точки E и D так, что АЕ=АС; ВD=ВС. Доказать, что  DCE равен 45○.
DCE равен 45○.
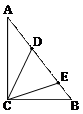 Решение: АЕ = АС =>
Решение: АЕ = АС =>  АСЕ =
АСЕ =  АЕС = 180○ –
АЕС = 180○ –  А; СВ = ВD =>
А; СВ = ВD =>  DCB =
DCB =  CDB =
CDB = 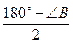
 DCF = 180○ – (
DCF = 180○ – (  CDB +
CDB +  CED) =
CED) = 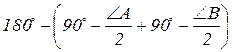 =
= 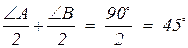 , т.к.
, т.к.  А +
А +  В = 90○.
В = 90○.
2. Доказать, что биссектрисы углов, прилежащих к одной из непараллельных сторон трапеции, пересекаются под прямым углом в точке, лежащей на средней линии трапеции.
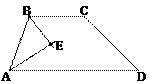 Решение: АВСD – трапеция.
Решение: АВСD – трапеция.  А+
А+  В=180○. АЕ – биссектриса
В=180○. АЕ – биссектриса  А; ВЕ – биссектриса
А; ВЕ – биссектриса  В =>
В =>  ЕВА+
ЕВА+  ВАЕ =1/2
ВАЕ =1/2  А+1/2
А+1/2  В =1/2 (
В =1/2 (  А+
А+  В) =1/2·180○ = 90○. В ∆АВЕ
В) =1/2·180○ = 90○. В ∆АВЕ  ВЕА=90○. Поскольку точка Е принадлежит биссектрисе угла А => Е равноудалена от АВ и АD; Е принадлежит
ВЕА=90○. Поскольку точка Е принадлежит биссектрисе угла А => Е равноудалена от АВ и АD; Е принадлежит
биссектрисе  В => Е равноудалена от АВ и ВС, т.е. Е равноудалена от ВС и АD, т.е. Е принадлежит средней линии трапеции АВСD.
В => Е равноудалена от АВ и ВС, т.е. Е равноудалена от ВС и АD, т.е. Е принадлежит средней линии трапеции АВСD.
3. Найдите корни уравнения, зная, что они являются противоположными числами: 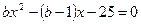 .
.
Решение: Т.к. уравнение имеет два различных корня, то 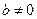 и
и 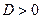 ;
; 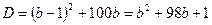
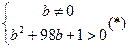 Т.к. x1+x2=0, то
Т.к. x1+x2=0, то 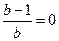 ;
; 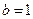 (условия (*)) выполняются.
(условия (*)) выполняются.
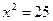 ;
; 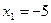 ;
; 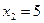
4. Найдите наибольшее целое решение неравенства: 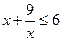 .
.
 Решение:
Решение: 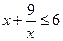 ;
; 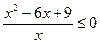 ;
; 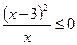
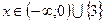
Ответ: x=3.
5. В одном бидоне на 5 л молока больше, чем в другом. Если из первого бидона перелить во второй 8 л молока, то во втором бидоне молока станет в 2 раза больше, чем останется в первом. Сколько литров молока в каждом бидоне?
Решение: Пусть x л молока в I бидоне, тогда 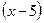 л во II бидоне.
л во II бидоне.
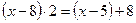
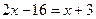 ; x=19.
; x=19.
Ответ: в I бидоне – 19л молока, во II – 14л.
ФИЗИКА
1. Программа по физике (8 класс)
1. Количество теплоты. Удельная теплоёмкость.
2. Агрегатные состояния вещества. Плавание и испарение.
3. Закон Сохранения и превращения энергии в механических и тепловых процессах.
4. Электрический ток. Источники электрического тока. Сила тока.
5. Электрическая цепь. Закон Ома для участка цепи.
6. Работа электрического тока.
7. Закон Джоуля-Ленца.
8. Распространение света. Закон отражения.
9. Преломление света. Линзы. Фокусное расстояние линзы
2. Программа по физике (9 класс; вопросы 8 класса + дополнительно)
10. Прямолинейное равноускоренное движение.
11. Относительное движение.
12. Равномерное движение по окружности.
13. Закон Ньютона.
14. Силы в природе.
15. Работа силы. Потенциальная энергия.
16. Закон сохранения импульса.
17. Закон сохранения полной механической энергии.
18. Колебательное движение (пружинный маятник, математический маятник).
19. Превращения энергии при колебательном движении.
3. Экзаменующийся должен уметь:
1. Изображать в виде рисунка или схемы физические процессы и явления.
2. Выявлять основные и второстепенные парные взаимодействия тел по условию задачи, проводить физический анализ; записывать решения в виде системы алгебраических уравнений, соответствующих физических законов.
3. Решать систему уравнений и неравенств.
4. Проводить физический анализ решения задачи.
4. Решение типовых задач:
1. После того как равномерно движущийся автомобиль начал торможение, его движение описывается уравнением х = 10 t - t2. Сколько времени двигался автомобиль до остановки и какой он при этом прошёл путь?
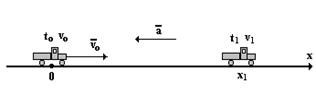 Дано:
Дано:
 х=10t-t2
х=10t-t2
а=const Графическое решение:
 t1-? x1-?
t1-? x1-?
Уравнение равнозамедленного движения:
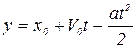 ,
, 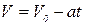 ; тогда х0=0, V0=10 м/с, а=2 м/с2.
; тогда х0=0, V0=10 м/с, а=2 м/с2.
Физическое решение: 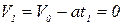 ,
, 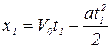 ;
;
Математическое решение:
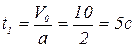 ,
, 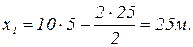
2. Камень падает в шахту. Через 6 секунд слышен стук камня о дно шахты. Определить глубину шахты, если скорость звука равна 330 м/с.
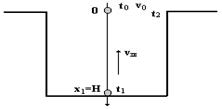 Дано:
Дано:
 t2=6 c
t2=6 c
Vзв =330 м/с Графическое решение:
 Н - ?
Н - ?
Физическое решение: 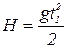 ,
, 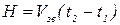 ;
;
Математическое решение:
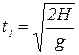 ,
, 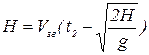 ,
, 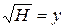 ,
, 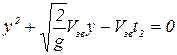
Физический корень:
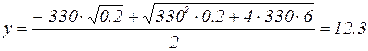 , H = 153 (м ).
, H = 153 (м ).
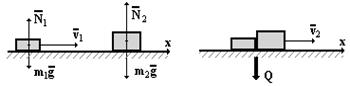
3. На покоящееся тело массой 3 кг налетает со скоростью 40 м/с другое тело массой 1 кг. Тела слипаются и продолжают движение вместе. Сколько механической энергии перешло в тепло?

 Дано:
Дано:
m1=1 кг
m2=3 кг Графическое решение:
V1=40 м/с
 Q-?
Q-?
Сумма внешних сил в проекции на ось х равно нулю, поэтому при взаимодействии тел проекции полного импульса на ось х сохраняется.
Физическое решение:
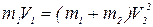
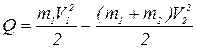
Математическое решение:
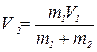 ,
, 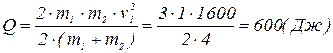
4. Электрическое сопротивление медной проволоки 8 Ом. Каким будет сопротивление, если проволоку сложить вдвое?
 Дано: Решение:
Дано: Решение:
 R=8 Ом Сопротивление провода находится по формуле
R=8 Ом Сопротивление провода находится по формуле 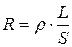 , где
, где
Rx-? 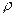 - удельное сопротивление,
- удельное сопротивление,
тогда: 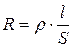
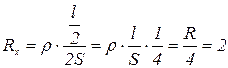 (Ом)
(Ом)
5. 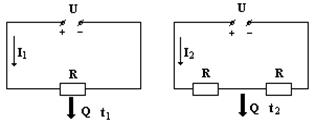 Один электрический нагреватель при подключении к источнику с нагреванием V выделяет количество теплоты Q за 12 минут. За какое время выделяет такое же количество теплоты два таких нагревателя, подключённых последовательно к источнику с тем же напряжением?
Один электрический нагреватель при подключении к источнику с нагреванием V выделяет количество теплоты Q за 12 минут. За какое время выделяет такое же количество теплоты два таких нагревателя, подключённых последовательно к источнику с тем же напряжением?
 Дано:
Дано:
t1=12 мин Графическое решение:
 t2 - ?
t2 - ?
