Метод последовательных итераций

Практическая работа № 6

Тема: «Классы и объекты»

Примеры решения задач

Здесь рассматриваются некоторые задачи, при решении которых применя­ются принципы объектно-ориентированного программирования.

Вычисление логарифма

В листинге 1.1 приведен пример программного кода, в котором для вычис­ления натурального логарифма по формуле 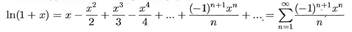создается специальный класс. У класса два поля и метод для вычисления логарифма. Что касается полей, то в одно поле (поле double х) заносит­ся значение аргумента x для выражения ln(1 + x), а второе поле (поле int N) определяет верхнюю границу N суммирования в выражении 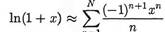(таким образом, у метода класса Ln () аргу­мента нет).

Листинг 1.1. Вычисление логарифма

#include <iostream>

#include <cmath>

using namespace std;

class MyLog{

public:

double x;

int N;

double Ln(){

double s=0,q=x;

int i;

for(i=l;i<=N;i++){

s+=q/i;

q*=-x;}

return s;}

} ;

int main(){

MyLog a;

cout«"Enter x = “;

cin»a. x;

cout«"Enter N = ";

cin»a. N;

cout«"ln ( "«l+a.x«") = "<<a. Ln () «endl;

cout«" ln ( "<<l+a.x<<") = "<<log (1+a. x) <<endl;

return 0;}

Результат выполнения программы может иметь следующий вид (жирным шрифтом выделен ввод пользователя):

Enter х =0.5

Enter N = 10

ln(1.5) = 0.405435

ln(1.5) = 0.405465

Для сравнения в последней строке приведен результат вычисления нату­рального логарифма с помощью встроенной функции.

Модуль и аргумент комплексного числа

Создадим класс для реализации комплексных чисел. Класс содержит два поля - действительная и мнимая части комплексного числа, а также мето­ды для вычисления модуля и аргумента комплексного числа. Последние две характеристики вычисляются на основании значения полей класса. Напомним, что в алгебраической форме записи любое комплексное число может быть представлено в виде 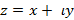, где действительные числа 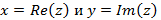соответственно действительная и мнимая части комплексного числа z, мнимая единица 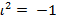. Это же число может быть записано в тригонометрическом представлении как 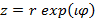, где модуль комплексного числа 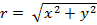, а аргумент 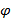таков, что 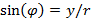и 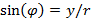. Программный код, в котором описан класс для реализации комплексных чисел, представлен в листинге 1.2.

Листинг 1.2. Модуль и аргумент комплексного числа

#include <iostream>

#include <cmath>

using namespace std;

class Compl{

public:

double Re;

double Im;

double modul(){

double r;

r=sqrt(Re*Re+Im*Im);

return r;}

double argument(){

double phi;

phi=atan2(Re,Im};

return phi;}

};

int mam () {

Compl z;

z.Re=sqrt(3);

z.Im=-1;

cout<<"|z| = "«z . modul () «endl ;

cout<<"phi = "«z . argument () «endl;

return 0; }

Схема Бернулли

Схемой Бернулли называется последовательность независимых испытаний с вероятностью «успеха» в одном испытании, равном p. Если серия состоит из п опытов, то вероятность того, что будет иметь место ровно т «успе­хов», дается выражением 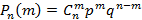, где биномиальный коэффициент 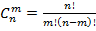, а вероятность «неудачи» q=1-p.

Создадим класс, в котором вероятность успеха в одном опыте будет опре­деляться значением поля класса, результат отдельного «опыта» будет мо­делироваться специальным методом. В качестве значения методом воз­вращается значение 0 («неудача» с вероятностью q=1-p) и 1 («успех» с вероятностью р). Для определения результата (количества успехов) в се­рии опытов упомянутый метод переопределим так, что если ему передается аргумент (целое число, определяющее количество опытов в серии), то ме­тодом возвращается количество успехов в такой серии. Соответствующий программный код представлен в листинге 1.3.

Листинг 1.3. Схема Бернулли

#include <iostream>

#include <cstdlib>

using namespace std;

class Bernoulli{

public:

double p;

int test(){

int N=1000;

int xi;

xi=rand()%N;

if (xi<p*N) return 1;

else return 0;}

int test(int n){

int s=0,i;

for(i=l;i<=n;i++) s+=test();

return s;}

};

int main(){

int i;

Bernoulli obj;

obj.p=0.3;

for (i=l; i<=9; i++) cout«obj.test() << “ “;

cout<<endl;

for (i=l; i<=9; i++) cout<<i*100<<": "«obj.test(i*l00)«endl;

return 0;}

Программой сначала проводится серия из 9 опытов - при успехе отобража­ется 1, а при неудаче отображается 0. Далее отображается количество успе­хов в серии из 100, 200 и т.д. до 900 включительно опытов. Результат может иметь следующий вид:

100: 21

200: 55

300: 100

400: 125

500: 125

600: 205

700: 203

800: 252

900: 286

Стоит обратить внимание, что при перегрузке метода test () (версия ме­тода с целочисленным аргументом) используется вызов этого же метода, но без аргумента. О рекурсии в данном случае речь не идет, поскольку вызыва­ется иная версия метода. Также обращаем внимание читателя, что в данном случае вычисляется «экспериментальное» количество успехов, поэтому от запуска к запуску результат выполнения программы может меняться. Чита­тель может взять себе на заметку, что в пределе при увеличении количества опытов в серии до бесконечности отношение количества успехов к количе­ству опытов в серии стремится к величине р (математическое ожидание количества успехов в схеме Бернулли из п опытов равняется пр). В дан­ном случае вероятность успеха р = 0.3. Правда, чтобы получить частоту успехов, близкую к указанному значению, необходимо выбрать число для количества опытов в схеме на несколько порядков больше, чем те, что ис­пользовались в программе.

Метод последовательных итераций

Вернемся к задаче по вычислению корня уравнения х = φ(x) методом по­следовательных итераций. Для этого создадим класс, полями которого бу­дут начальное приближение и общее число итераций. У класса также будет два метода: метод, определяющий зависимость φ(х), и метод, с помощью которого реализуется итерационный процесс 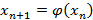.Программный код приведен в листинге 1.4.

Листинг 1.4. Метод последовательных итераций

#include <iostream>

#include <cmath>

using namespace std;

class Eqns{

public:

double xO;

int n;

double phi(double x){

return 0.8*cos(x);}

double root(){

double s=x0; int 1;

for (i=l; K=n; i++) s=phi(s);

return s;}

} ;

int main(){

Eqns obj;

obj.x0=0 ;

obj.n=100;

cout«"x = "«obj.root()«endl;

return 0;}

В данном случае решается уравнение х = 0.8cos(x). Программой вычис­ляется следующее значение для корня:

х = 0.641134

Результат получен для 100 итераций с нулевым начальным приближением для корня уравнения.

Полет тела

Решим задачу о полете тела, брошенного под углом к горизонту, с помощью методов объектно-ориентированного программирования. Здесь создадим специальный класс, полями которого будут начальная скорость и угол, под которым тело брошено к горизонту. Методами класса будут вычисляться координаты (горизонтальная и вертикальная) проекции скорости на коор­динатные оси. Программный код приведен в листинге 1.5.

Листинг 1.5. Полет тела

#include <iostream>

#include <cmath>

using namespace std;

const double g=9.8;

const double pi=3.1415;

class Body{

double T(){

return 2*V0*sin(alpha)/g;}

public:

double VO;

double alpha;

double x(double t){

if(t<=T()) return V0*cos(alpha)*t;

else return V0*cos(alpha)*T();}

double у(double t){

if(t<=T()) return V0*sin(alpha)*t-g*t*t/2;

else return 0; }

double Vx(double t){

if(t<=T()) return V0*cos(alpha);

else return 0; }

double Vy(double t){

if(t<=T()) return V0*sin(alpha)-g*t;

else return 0;}

void show(double t)(

printf("%s%f%s%9f%s%9f%s%9f%s%9f%s","t=",t,": x=",x(t)," y⁼"/у(t)," Vx=",Vx(t), " Vy=",Vy(t),"\n");}

} ;

int main(){

int i;

Body obj;

obj.V0=10;

obj.alpha=pi/3;

for(i=0;i<10;i++) obj.show(0.2*i);

return 0;}

В программе объявлены две глобальные константы - число π и ускорение свободного падения. Основной функциональный блок программы реали­зуется через класс Body. В этом классе описан закрытый метод T(), ко­торым на основе полей V0 (начальная скорость тела) и alpha (угол, под которым тело брошено к горизонту) типа double вычисляется время по­лета тела. Этот важный показатель необходим для вычисления положения тела в произвольный момент времени. Координаты тела и скорость (про­екции на координатные оси) тела вычисляются методами х(), у(), Vx() и Vy(). При вычислениях использованы следующие соотношения: время полета тела, брошенного с начальной скоростью V₀ под углом α к горизонту 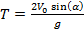, проекция скорости тела на горизонтальную координатную ось V_x(t) = V₀ cos(α) при t < Т и V_x(t) = 0 при t > Т (тело упало), на вертикальную ось V_y(t) = V₀ sin(α) — gt при t < T и V_y(t) = 0 при t > Т (тело упало), координаты тела x(t) = V₀ cos(α)t при t < T и x(t) = V₀ cos(a)T при t > T, 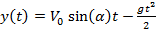при t < T и y(t) = 0 при t > T. В главном методе программы выводится таблица зна­чений координат и скоростей для разных моментов времени. Результат вы­полнения программы имеет следующий вид:

t=0.000000: х=0.000000 у=0.000000 Vx=5.000267 Vy=8.660100

t=0.200000: х=1.000053 у=1.536020 Vx=5.000267 Vy=6.700100

t=0.400000: x=2.000107 y=2.680040 Vx=5.000267 Vy=4.740100

t=0.600000: x=3.000160 y=3.432060 Vx=5.000267 Vy=2.781100

t=0.800000: x=4.000214 y=3.792080 Vx=5.000267 Vy=0.820100

t=l.000000: x=5.000267 y=3.760100 Vx=5.000267 Vy=-1.139900

t=l.200000: x=6.000321 y=3.336120 Vx=5.000267 Vy=-3.099900

t=l.400000: x=7.000374 y=2.520139 Vx=5.000267 Vy=-5.059900

t=l.600000: x=8.000428 y=1.312159 Vx=5.000267 Vy=-7.019900

t=l.800000: x=8.837309 y=0.000000 Vx=0.000000 Vy=0.000000

Стоит обратить внимание на использование в данном случае для вывода данных функции printf (). Первым аргументом функции указана строка, определяющая формат вывода. В этой строке инструкция %s означает вы­вод текстового блока, инструкция % f используется для индикации вывода числа с плавающей точкой. Цифра между символом процента % и буквой f определяет минимальное количество позиций для вывода числа. Сами вы­водимые на экран блоки (текст и числа) перечислены через запятую сле­дующими после первого аргументами функции printf ().