Уравнивание координат точек хода
Порядок вычислений
1.2.1. Вычисление приращений координат с учетом угла разворота хода (табл. 5):
1.2.1.1. Из табл. 3 выписать горизонтальные проложения 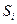 и длину хода
и длину хода 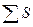 .
.
1.2.1.2. Из табл. 4 выписать дирекционные углы линий хода с учетом разворота 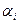 .
.
1.2.1.3. Вычислить приращения координат с учетом угла разворота хода:
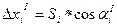 ;
;
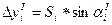 .
.
Таблица № 5
Вычисление приращений координат с учетом угла разворота хода
| № точек | 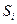 | 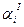 | 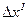 | 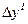 |
| п. 225 | ||||
| ст. 1 | ||||
| ст. 2 | ||||
| ст. 3 | ||||
| ст. 4 | ||||
| п. 216 |
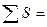
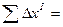
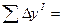
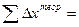
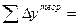
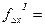
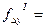
1.2.1.4. Вычислить практические ( 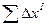 и
и 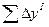 ) и теоретические (
) и теоретические ( 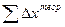 и
и 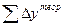 ) суммы приращений координат.
) суммы приращений координат.
1.2.1.5. Вычислить невязки по осям координат:
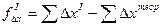 ;
;
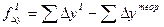 .
.
1.2.2. Приближенное уравнивание приращений координат развернутого хода (табл. 6).
1.2.2.1. Из табл. 1 исходных данных выписать значения координат согласно номеру своего варианта.
1.2.2.2. Из табл. 5 выписать приращения координат с учетом угла разворота хода 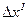 и
и 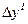 .
.
1.2.2.3. Вычислить поправки в приращения координат развернутого хода:
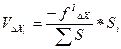 ;
;
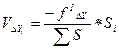 , где
, где
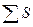 и
и 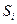 - длина хода и горизонтальные проложения (табл. 5).
- длина хода и горизонтальные проложения (табл. 5).
1.2.2.4. Контроль вычисления поправок в приращения координат развернутого хода:
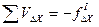 ;
;
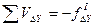 .
.
1.2.2.5. Вычислить исправленные приращения координат развернутого хода и найти 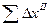 и
и 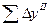 :
:
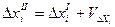 ;
;
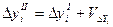 .
.
1.2.2.6. Контроль вычислений исправленных приращений координат развернутого хода:
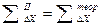
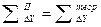 .
.
1.2.2.7. Вычисление координат точек развернутого хода:
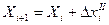 ;
;
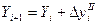 .
.
Таблица № 6
Вычисление координат развернутого хода
| № т. | 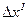 | 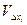 | 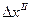 | 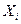 | 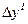 | 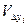 | 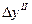 | 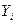 |
| п. 225 | ||||||||
| ст. 1 | ||||||||
| ст. 2 | ||||||||
| ст. 3 | ||||||||
 ст. 4 ст. 4 | ||||||||
| п. 216 |
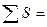
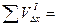
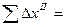
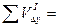
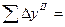
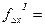
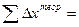
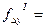
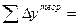
| |
Вычисление высот точек хода
Порядок вычислений
1.3.1. В ведомость вычисления высот (табл. 8) выписать горизонтальные проложения 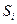 (табл. 3), превышения
(табл. 3), превышения 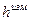 (табл. 7), а также высоты H225 и Н216 согласно номеру своего варианта (табл. 1).
(табл. 7), а также высоты H225 и Н216 согласно номеру своего варианта (табл. 1).
Таблица № 7
Таблица измеренных превышений
| № точки | 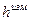 , м , м |
| п. 225 | |
| -0,179 | |
| ст. 1 | |
| -0,503 | |
| ст. 2 | |
| +0,558 | |
| ст. 3 | |
| -0,180 | |
| ст. 4 | |
| +3,494 | |
| п. 216 |
1.3.2. Вычислить невязку в превышениях хода:
 , где
, где
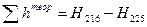
и сравнить данную невязку с её допустимым значением:
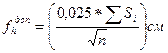 , где
, где
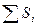 – длина хода;
– длина хода;
n – количество превышений в ходе.
1.3.3. Вычислить поправки в измеренные превышения:
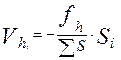 .
.
1.3.4. Контроль вычисления поправок в превышения:
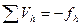 .
.
1.3.5. Вычислить уравненные значения превышений:
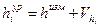 .
.
1.3.6. Контроль вычисления уравненных превышений:
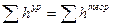 .
.
1.3.7. Вычислить высоты точек хода:
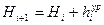
Таблица № 8
Ведомость вычисления высот точек хода
| № точки | 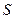 , м , м | 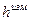 , м , м | 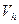 , м , м | 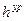 , м , м | 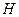 , м , м |
| п. 225 | |||||
| Ст. 1 | |||||
| Ст. 2 | |||||
| Ст. 3 | |||||
| Ст. 4 | |||||
| п. 216 |
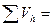
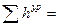
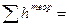
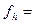
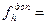
2. ОПРЕДЕЛЕНИЕ КООРДИНАТ
ДОПОЛНИТЕЛЬНЫХ ПУНКТОВ
2.1. Прямая угловая засечка (имеется видимость между
исходными пунктами)
Прямая угловая засечка – это задача по определению координат третьего пункта (Р1) по координатам двух исходных пунктов (ст.3 и ст.4) и двум измеренным углам при исходных пунктах ( 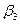 и
и 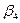 ) (рис. 2.1).
) (рис. 2.1).
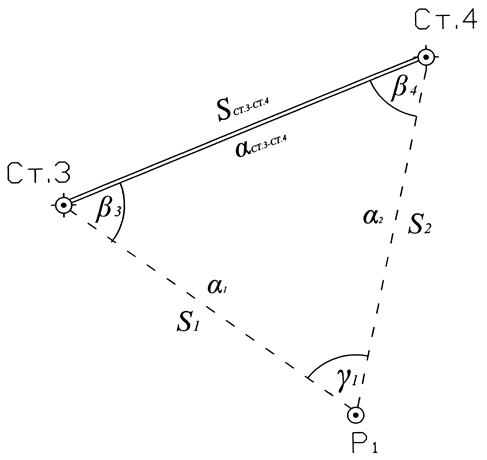
Рис. 2.1. Схема прямой угловой засечки
Дано: 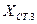 ,
, 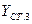 ;
;
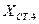 ,
, 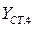 .
.
Измерено: 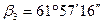 ;
;
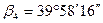 .
.
Найти: 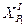 ,
, 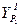 .
.
Порядок вычислений
2.1.1. По известным координатам пунктов ст.3 и ст.4 (табл. 6) найти 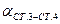 и
и 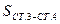 из решения обратной геодезической задачи.
из решения обратной геодезической задачи.
2.1.2. По измеренным горизонтальным углам 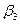 и
и 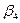 вычислить дирекционные углы
вычислить дирекционные углы 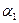 и
и 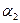 :
:
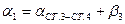 ;
;
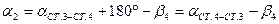 .
.
2.1.3. Из решения треугольника ст.3–ст.4–P1 (по теореме синусов) найти горизонтальные проложения 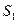 и
и 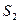 :
:
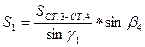 ;
;
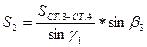 , где
, где
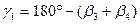 .
.
2.1.4. Вычислить координаты определяемого пункта 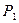 :
:
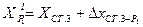 ;
;
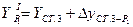 , где
, где
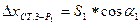 ;
;
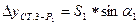 .
.
2.1.5. Контроль вычисления координат определяемого пункта P1:
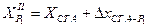 ;
;
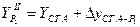 ,
,
где
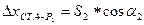 ;
;
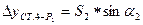 .
.
2.1.6. Контроль считается выполненным, если координаты определяемого пункта P1 совпадут.
Если контроль выполняется, то записать окончательные значения координат определяемого пункта 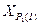 и
и 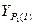 .
.
Вычисления выполнить в табл. 9.
2.1.7. Оценка точности положения определяемого пункта P1:
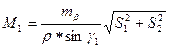 , где
, где
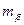 – СКП измерения горизонтального угла (
– СКП измерения горизонтального угла ( 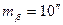 ,
, 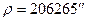 ).
).
Таблица № 9
Определение координат пункта P1
(имеется видимость между исходными пунктами)
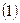 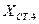 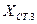 | 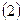 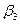 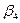 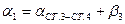 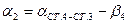 | ||
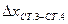 | |||
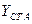 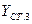 | |||
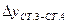 | 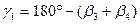 | ||
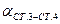 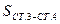 | 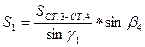 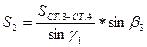 | ||
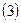 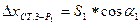 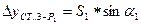 | 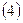 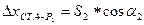 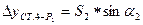 | ||
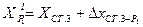 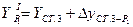 | 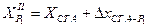 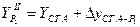 | ||
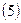 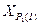 | 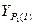 |
2.2. Прямая угловая засечка (отсутствует взаимная
видимость между исходными пунктами)
Между исходными пунктами ст.1 и ст.3 нет взаимной видимости, измерены горизонтальные углы 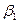 и
и 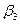 (рис. 2.2).
(рис. 2.2).
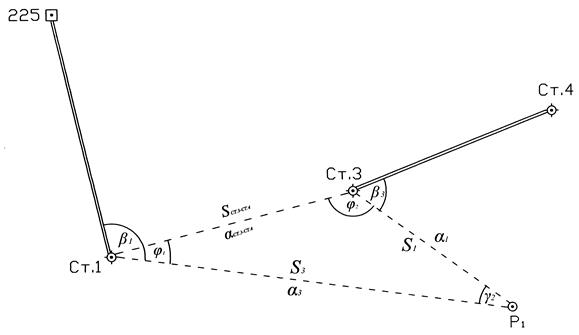
Рис. 2.2. Схема прямой угловой засечки
Дано: 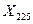 ,
, 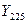 ;
;
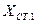 ,
, 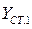 ;
;
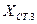 ,
, 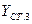 ;
;
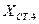 ,
, 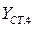 .
.
Измерено: 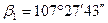 ;
;
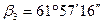 .
.
Найти: 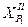 ,
, 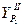 .
.
Порядок вычислений
2.2.1. По известным координатам пунктов 225, ст.1, ст.3 и ст.4 (табл. 1 и табл. 6) найти 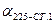 ,
, 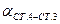 ,
, 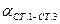 и
и 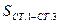 из решения обратной геодезической задачи.
из решения обратной геодезической задачи.
2.2.2. По измеренным горизонтальным углам 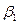 и
и 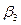 вычислить дирекционные углы
вычислить дирекционные углы 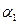 и
и 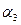 .
.
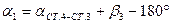 ;
;
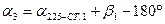 .
.
2.2.3. Вычислить горизонтальные углы 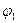 и
и 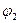 :
:
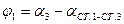 ;
;
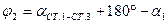 .
.
2.2.4. Из решения треугольника ст.1–ст.3–P1 (по теореме синусов) найти горизонтальные проложения 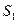 и
и 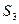 :
:
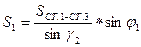 ;
;
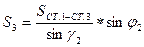 , где
, где
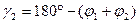 .
.
2.2.5. Вычислить координаты определяемого пункта Р1:
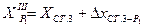 ;
;
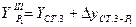 , где
, где
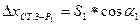 ;
;
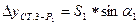 .
.
2.2.6. Контроль вычисления координат определяемого пункта Р1:
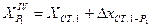 ;
;
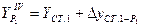 , где
, где
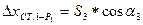 ;
;
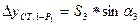 .
.
2.2.7. Контроль считается выполненным, если координаты определяемого пункта P1 совпадут.
Если контроль выполняется, то записать окончательные значения координат определяемого пункта 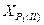 и
и 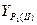 .
.
Вычисления выполнить в табл. 10.
2.2.8. Оценка точности положения определяемого пункта Р1.
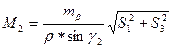 , где
, где
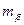 – СКП измерения горизонтального угла (
– СКП измерения горизонтального угла ( 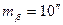 ,
, 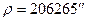 );
);
Таблица № 10
Определение координат пункта P1 (отсутствует видимость
между исходными пунктами)
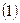 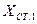 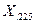 | 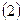 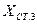 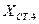 | ||
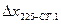 | 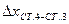 | ||
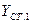 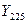 | 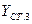 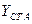 | ||
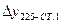 | 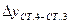 | ||
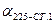 | 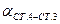 | ||
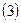 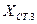 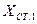 | 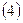 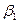 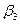 | ||
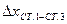 | 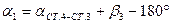 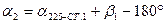 | ||
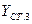 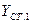 | 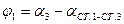 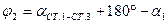 | ||
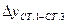 | 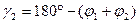 | ||
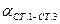 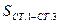 | 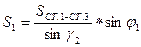 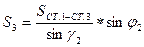 | ||
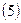 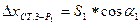 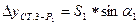 | 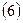 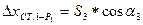 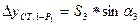 | ||
 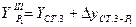 | 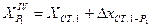 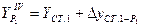 | ||
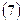 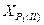 | 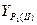 |
2.3. Вычисление окончательных значений координат
определяемого пункта P1.
Порядок вычислений
2.3.1. Выписать в табл. 11 результаты вычисления координат определяемого пункта Р1,полученные из решения прямой угловой засечки для случаев наличия или отсутствия взаимной видимости между исходными пунктами (табл. 9 и табл. 10).
Таблица № 11
Вычисление окончательных координат пункта Р1
| Координаты (м) | Расхождение, м | ||
| Имеется видимость | Отсутствует видимость | Среднее | |
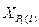 = = | 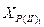 = = | 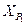 = = | 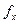 = = |
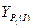 = = | 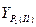 = = | 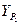 = = | 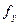 = = |
2.3.2. Вычислить невязки по осям координат:
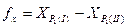 ;
;
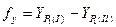 .
.
2.3.3. Вычислить линейную невязку и сравнить её с допустимой линейной невязкой:
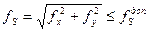 , где
, где
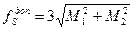 , где
, где
М1 – СКП положения пункта Р1 из решения прямой угловой засечки при наличии взаимной видимости между исходными пунктами;
М2 – СКП положения пункта Р1 из решения прямой угловой засечки при отсутствии взаимной видимости между исходными пунктами.
2.3.4. Если линейная невязка fS допустима, то найти окончательные значения координат:
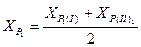 ;
;
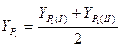 .
.
