В курсе физики средней школы

ПОЛЯРИЗАЦИЯ ВОЛН

Как защитить водителя автомобиля от слепящего действия света фар встречного автомобиля? Как рыбаку на море и фотографу в студии устранить зеркальные блики? Почему при определенном освещении лобовое стекло троллейбуса кажется пятнистым, а при аварии оно рассыпается на кусочки, размеры которых одинаковы с размерами пятен? Как конструктору новой техники определить места концентрации механических напряжений в нагруженных деталях машин, а мостостроителям до начала строительства моста испытать его конструкцию с помощью модели, выполненной из оргстекла? Как определить оптическое качество выращиваемых кристаллов? Как быстро определить концентрацию сахарного раствора на плодоовощном комбинате? Как фармацевту отличить обладающий лечебным действием препарат от его зеркально симметричного по строению и абсолютно бесполезного для больного «брата-близнеца»? Как выяснить, обладает ли собственным магнитным полем небесное тело, долететь до которого нельзя? Как измерить большие токи и напряжения? Как сформировать сверхкороткие (с длительностью ~ 10^-9 – 10^-15 с) световые импульсы? Каким образом кодировать изображения и сигналы, например, для целей стереоскопического видения плоских изображений? Как обеспечить выполнение логических операций в сверхбыстродействующих вычислительных машинах? Как получить информацию о кинетике свертывания крови, о свойствах белковых молекул, биологических мембран, кристаллов, полупроводниковых и металлических веществ?

Ответить на эти и многие другие вопросы можно, хорошо познакомившись с явлением поляризации волн, свойствами поляризованного излучения и особенностями его взаимодействия с различными веществами как в отсутствие, так и при наличии внешних полей (механических напряжений, электрических или магнитных воздействий). Однако, к сожалению, эту очень важную как с образовательной, так и с профориентационной точки зрения тему авторы школьных учебников излагают лишь качественно, давая отрывочные сведения только о линейной поляризации и только световых волн. Вопросы же практического применения поляризации волн не обсуждаются вовсе.

Главные цели предлагаемой лекции, содержание которой может быть предложено учащимся классов с углубленным изучением физики, следующие:

· познакомить учащихся с основными поляризационными явлениями и историей их открытия; убедить учащихся, что поляризация – свойство любых по природе поперечных волн;

· опираясь на математические знания учащихся, сформировать у них чёткие представления о типах и формах поляризации;

· познакомить школьников с методикой анализа поляризованных пучков и областями практического применения изучаемого явления.

Опыты и демонстрации, сопровождающие лекцию, могут быть выбраны учителем с учётом возможностей школьного физкабинета, а часто – изготовлены из подручных средств.

Явление поляризации света было открыто Эразмусом Бартолинусом, датским учёным, в 1669 году. В своих опытах Бартолинус использовал кристаллы исландского шпата ( 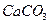), имеющие форму ромбоэдра. Если на такой кристалл падает узкий пучок света, то, преломляясь, он даёт два пучка несколько различного направления (рис. 3.1).

Если падающий пучок довольно узок, а кристалл достаточно толст, то из него выходят два пучка, параллельных первоначальному, вполне разделенных пространственно. Даже в том случае, когда первичный пучок перпендикулярен к естественной грани кристалла, преломленный пучок разделяется на два (рис. 3.2), причем один из них представляет продолжение первичного, а второй уклоняется так, что угол преломления отличен от нуля. Это обстоятельство и ряд других отступлений от обычных законов преломления дали повод назвать второй из этих лучей необыкновенным (е), сохраняя за первым название обыкновенного (о). 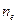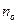Различие в отклонении обоих лучей показывает, что по отношению к ним кристалл имеет различные показатели преломления ( и соответственно) и скорости волн ( 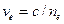; 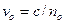). Исследуя явление при различных направлениях преломленных лучей внутри кристалла, можно обнаружить, что обыкновенный луч имеет для всех направлений один и тот же показатель преломления, а показатель преломления необыкновенного луча зависит от направления. При вращении кристалла необыкновенный луч перемещается вокруг обыкновенного по окружности (рис. 3.2). Описанное явление назвали дву(луче)преломлением.

В 1690 году Христиан Гюйгенс, голландский учёный, обнаружил, что каждый из полученных указанным способом лучей ведёт себя при прохождении через второй кристалл исландского шпата иначе, чем обычные лучи. В зависимости от ориентации кристаллов относительно друг друга каждый из лучей, раздваиваясь во втором кристалле, даёт два луча различной интенсивности, а при некоторых ориентациях – только один луч, а интенсивность второго в этом случае падает до нуля (рис. 3.3).

В 1808 году, наблюдая через кристалл исландского шпата свет, отраженный под большим углом от окна Люксембургского дворца в Париже, французский учёный Этьен Луи Малю заметил, что при повороте кристалла вокруг луча интенсивность двух получающихся при этом пучков периодически меняется: 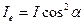, , 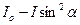где 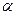- угол между главными направлениями кристаллов-поляризаторов, 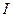- интенсивность падающего пучка. Кроме того, для интенсивностей о- и е – лучей в отсутствие поглощения выполняются правила Малю: 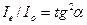; 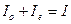. Именно Малю ввёл в обращение термин поляризация света.

Подчеркнём сразу, что поляризация свойственна любым по природе, но только поперечным волнам.

Гипотезу о поперечности световых волн впервые высказал Роберт Гук, английский физик, в 1757 году. После установления волновой природы света явление поляризации подверглось дальнейшему тщательному изучению. В 1816 году Огюст Френель, французский физик, установил, что два луча, поляризованных взаимно перпендикулярно, не могут интерферировать. Опыты Френеля и Араго (французский учёный) по интерференции поляризованных лучей побудили Томаса Юнга, английского физика, высказать догадку о поперечности световых волн (1817 год). Френель, независимо от Юнга, также выдвинул конпепцию поперечности световых волн, всесторонне обосновал её многочисленными важными опытами и положил в основу объяснения явления поляризации света и двойного лучепреломления в кристаллах. Учение Френеля о поперечных световых волнах дало толчок к исследованию свойств упругих твёрдых тел. Однако применение полученных знаний в оптике привело к ряду принципиальных затруднений, связанных с несовместимостью законов механических колебаний упругой среды и наблюдаемых на опыте законов оптических явлений. Эти затруднения были устранены только с появлением электромагнитной теории света, в которой на основании уравнений Максвелла была доказана поперечность электромагнитных волн.

Однако отсутствие интерференционного чередования интенсивностей при сложении двух взаимно перпендикулярных колебаний, зарегистрированное в опытах Френеля, не означает, что взаимодействие таких колебаний не может приводить к доступным наблюдению на опыте изменениям в световом пучке.

Рассмотрим результат сложения двух когерентных световых волн, поляризованных в двух взаимно поляризованных направлениях, имеющих разную амплитуду и обладающих некоторой разностью фаз. Мы легко можем осуществить такую ситуацию на опыте следующим образом (рис. 3.4).

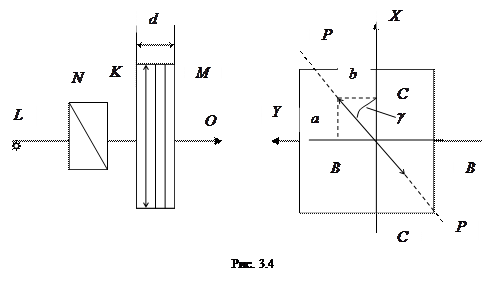Свет определенной длины волны, прошедший через поляризующее устройство 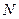и ставший линейно поляризованным, пропустим через кристаллическую пластинку 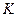толщиной 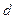, вырезанную из одноосного кристалла (то есть из кристалла, имеющего лишь одно направление, называемое оптической осью, в котором скорости обыкновенной и необыкновенной волн одинаковы) параллельно его оптической оси. Допустим при этом, что направление пучка перпендикулярно к боковой поверхности кристалла 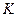. Сквозь пластинку будут распространяться в одном направлении, но с разной скоростью две волны, поляризованные во взаимно перпендикулярных направлениях, которые принято называть главными направлениями кристаллической пластинки. У одной из этих волн вектор 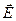колеблется вдоль оптической оси кристалла (например, вдоль 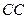колеблется 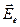, соответствующий необыкновенной волне, для которой показатель преломления равен 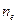), а у другой – перпендикулярно оптической оси (то есть вдоль 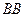; ; 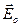обыкновенная волна; ).

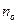Если направление колебаний электрического вектора в падающей поляризованной волне составляет угол 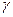с одним из главных направлений пластинки, то амплитуды колебаний в необыкновенной и обыкновенной волнах будут соответственно равны

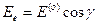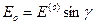; , (3.1)

где 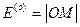(см. рис. 3.4) – амплитуда падающей волны.

Пройдя через толщу пластинки 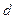, эти две волны приобретут разность хода, равную

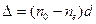. (3.2)

Следовательно, обыкновенная волна отстанет по фазе от необыкновенной на величину 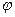, равную

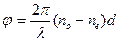. (3.3)

На выходе из кристалла 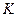произойдет сложение колебаний одинаковой частоты 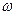, происходящих по законам

;

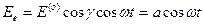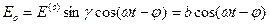. (3.4)

Определим траекторию конца вектора 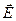для результирующего колебания. Для этого из формул (3.4) исключим время 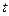. Получим:

,

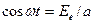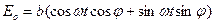(3.5)

или

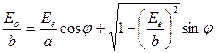. (3.6)

Возводя (3.6) в квадрат, после преобразований получим уравнение траектории, описываемой концом вектора :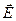

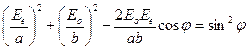, (3.7)

то есть уравнение эллипса.

Таким образом, после прохождения линейно поляризованного света через кристаллическую пластинку получаем в общем случае световую волну, концы векторов 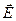и 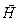которой описывают эллипсы. Световая волна, электрический вектор которой в фиксированной точке пространства вычерчивает один и тот же, регулярно повторяющийся эллипс, называется эллиптически поляризованной в этой точке. Эллиптическая поляризация – наиболее общее состояние поляризации любого строго монохроматического оптического поля.

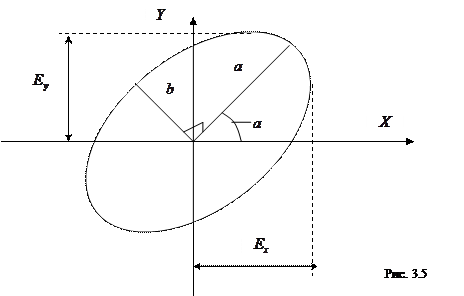Угол 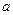(рис. 3.5), составленный большой полуосью эллипса с осью 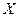, называется азимутом поляризации и может изменяться в пределах 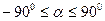. Отношение длин малой и большой полуосей эллипса 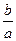называют эллиптичностью. Она изменяется в пределах от нуля ( 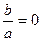, и свет называется линейно (или плоско-) поляризованным) до единицы ( 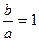, свет поляризован циркулярно, или по кругу). Угол эллиптичности 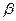, определяемый из условия 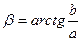, варьирует в пределах от 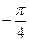до 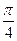. Величина 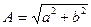называется амплитудой эллиптического колебания. Квадрат амплитуды колебаний пропорционален плотности энергии волны в точке наблюдения. Абсолютная фаза 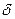эллиптически поляризованной волны определяет угол между начальным положением электрического вектора при 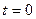и большой осью эллипса ( 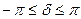). В зависимости от того, какая волна (обыкновенная или необыкновенная) распространяется быстрее, вектор 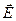результирующей волны будет перемещаться по или против хода часовой стрелки (смотреть нужно навстречу лучу). Свет при этом соответственно называется правоэллиптически поляризованным или левоэллиптически поляризованным.

Таким образом, существуют три типа поляризации волн: линейная, циркулярная, эллиптическая.

Для линейно поляризованного света 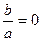и существует бесконечное число форм линейной поляризации, различающихся азимутом .

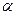Для циркулярно поляризованных волн 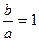, и существует две формы циркулярной поляризации: право- и левоциркулярно поляризованные волны.

Эллиптическая поляризация имеет бесконечное число форм, различных по азимуту, эллиптичности и направлению вращения вектора .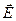

Два линейно поляризованных луча, азимуты поляризации которых отличаются на 90⁰, называют ортогонально поляризованными, если они распространяются в одном направлении. Право- и левоциркулярно поляризованные волны также ортогональны. Два эллиптически поляризованных пучка ортогональны, если азимуты главных направлений отличаются на 90⁰, направления вращения противоположны, а эллиптичности одинаковы.

Свет называется полностью поляризованным, если два взаимно ортогонально поляризованных компонента вектора 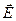светового пучка совершают колебаний с постоянной во времени разностью фаз. Если фазовое соотношение между компонентами вектора 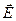изменяется за время, существенно меньшее времени измерения состояния поляризации, то свет проявляется как частично поляризованный. Состояние поляризации частично поляризованного света описывается параметром степени поляризации:

; ; .

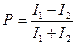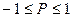Здесь 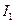и - и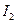нтенсивности ортогонально линейно поляризованных компонентов пучка, 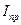и - и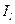нтенсивности право- и левоциркулярно поляризованных компонентов пучка соответственно. Для полностью поляризованного света .

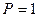Подводя итог сказанному выше, может определить следующее: поляризованный свет – это свет с преимущественным направлением колебаний: преимущественным для одного из поперечных направлений или для определенного направления вращения.

Каковы же способы получения поляризованного света?

Свет может быть поляризован в следующих случаях:

· при излучении элементарным источником (диполем);

· в результате двупреломления. Двупреломляющие поляризаторы разделяют первоначальный пучок на два полностью и ортогонально поляризованных компонента и устраняют один из них. Широко применяются в оптическом приборостроении такие двупреломляющие поляризаторы как призмы Николя (1828 г.), Аренса (1896 г.), Волластона, Рошона (1783 г.), Глана – Фуко и др.

Призма Волластона состоит из двух прямоугольных призм из исландского шпата, склеенных гипотенузными гранями. В призме АВС оптическая ось параллельна катету АВ; в призме АСD оптическая ось параллельна ребру С, перпендикулярному к плоскости чертежа (рисунок ).

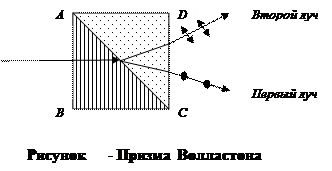Через грань АВ в призму входит естественный свет. Образовавшиеся вследствие двупреломления обыкновенный и необыкновенный лучи идут в первой призме в одном направлении с разными скоростям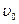и и 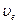. Во второй призме они также идут в направлении, перпендикулярном оптической оси, но так как оптические оси в обеих призмах взаимно перпендикулярны, то о-луч в первой призме превратится в е-луч во второй призме и наоборот. Для исландского шпата . Поэтому во второй призме первы луч отклонится в сторону ребра С, а второй – в сторону основания этой призмы АD – лучи разойдутся симметрично относительно направления падающего пучка. Оба выходящих пучка поляризованы: в первом луче (е-луч во второй призме) вектор 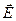колеблется параллельно оптической оси второй призмы, во втором (о-луч во второй призме) – перпендикулярно оптической оси второй призмы.

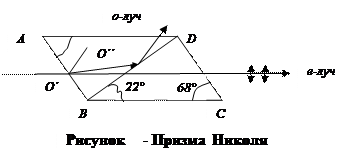Призма Николя (николь) состоит из двух прямоугольных призма из исландского шпата. Острые углы призмы равны 68° и 22°, призмы склеены канадским бальзамом вдоль катета ВС. Оптическая ось О´О´´ лежит в плоскости чертежа под углом 48° к грани АВ (и аналогично – во второй призме).

Падающий луч разделяется в первой призме на два, из которых один – обыкновенный – падает на слой канадского бальзама ВС под углом около 76°. Показатель преломления канадского бальзама n = 1,550 меньше показателя преломления обыкновенного луча (n_о = 1,658), угол падения превышает предельный, и обыкновенный луч испытывает полное внутреннее отражение на границе кристалл – канадский бальзам. Поэтому этот луч не попадает во вторую призму и выходит через грань АС. Необыкновенный луч имеет меньший показатель преломления чем канадский бальзам, поэтому он не испытывает полного внутреннего отражения и переходит во вторую призму. Таким образом, через призму проходит только необыкновенный луч. Обыкновенный луч может быть поглощен зачерненной оправой призм. Призма Николя пропускает полностью поляризованный свет в пучках с углом расхождения до 29°.

В сечении призма имеет вид ромба. В прошедшем пучке электрический вектор колеблется в направлении, параллельном короткой диагонали ромба.

Недостатком призмы Николя является непрозрачность канадского бальзама для ультрафиолетового излучения. Она применима только в видимой области спектра.

Призма из стекла и исландского шпата. Оптическая ось перпендикулярна плоскости чертежа; n_o = 1,66; n_стекла = 1,49; n_e = 1,486.

Призма Рошона из исландского шпата. Угол между ортогонально поляризованными лучами зависит от преломляющего угла призмы; обыкновенный луч ахроматичен.

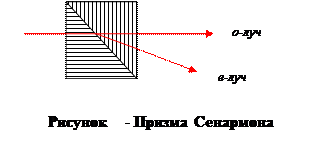
Призма Сенармона. Преломляющий угол близок к 45 °, поэтому удается экономно расходовать исходный кристалл, разрезая его вдоль оптической оси и склеивая вдоль естественной грани.

· как следствие дихроизма вещества, суть которого заключается в зависимости показателя поглощения излучения средой от состояния его поляризации. Пластинка из дихроичного вещества разделяет падающий пучок на два поляризованных компонента и поглощает их в различной степени. Если дихроичный материал раскалить, то в излучаемом свете будет преобладать та форма поляризации, которая преимущественно поглощается в этом материале. Первый пригодный для использования дихроичный поляроид был разработан Эдвином Лендом (1928 г.), 19-летним студентом Гарвардского университета. В 1938 г. им же были предложены дихроичные поляризаторы, в которых использовались особые свойства полимерных молекул. Поляроидные плёнки обеспечивают степень поляризации ;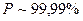

· при отражении от границы раздела сред;

· при прохождении границы раздела сред (при преломлении);

· при полном внутреннем отражении

Изменение фазы при полном внутреннем отражении можно использовать для получения циркулярно поляризованного света. В ромбе Френеля вследствие двукратного полного внутреннего отражения падающий линейно поляризованный свет преобразуется в циркулярно поляризованный.

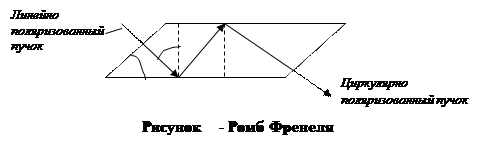Амплитуды ортогонально поляризованных составляющих падающего пучка уравнивают, выбирая направление поляризации падающего пучка под углом 45° к плоскости падения. Затем показатель преломления стекла и угол падения света на входную грань подбирают таким образом, чтобы относительная разность фаз δ была равна 90°. Если эти условия не выполнены, вышедший из ромба Френеля свет поляризован эллиптически.

При направлении на ромб Френеля эллиптически или циркулярно поляризованного пучка света можно преобразовать его в линейно поляризованный;

· при рассеянии излучения на неоднородностях среды;

· поляризовано излучение лазерных источников и т.д.

А как же отличить поляризованный свет от неполяризованного, поляризованный линейно от циркулярно или эллиптически поляризованного и т.п.?

Прежде чем предложить алгоритм анализа состояния поляризации пучка познакомимся с принципом действия фазовых пластинок, необходимых для указанного анализа.

Фазовая пластинка – это оптический элемент, который, не меняя интенсивности и степени поляризации монохроматического поляризованного пучка света, расщепляет его на два компонента, сдвигает фазу одного из них относительно другого и затем вновь соединяет компоненты в один пучок.

Пусть толщина пластинки 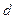такова, что разность хода упомянутых компонентов составляет 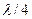(пластинка в четверть длины волны):

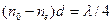
или

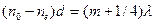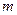, = 0, 1, 2, … (3.8)

В таком случае 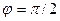, и уравнение эллипса (3.7) принимает вид:

,

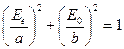то есть эллипс ориентирован относительно главных осей пластинки. Соотношение длин его полуосе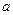й и 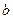зависит от угла 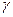. При 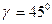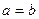и эллипс вырождается в окружность:

.

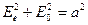В таком случае на выходе из пластинки свет поляризован циркулярно. Роль четвертьволновой пластинки для излучения соответствующего желтой линии натрия ( 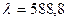нм) успешно выполняет пластинка из прозрачной слюды толщиной 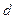= 0,027 мм.

Если же пластинка вносит разность хода, равную

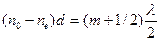, (3.9)

то 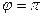или 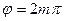, и эллипс вырождается в прямую

,

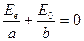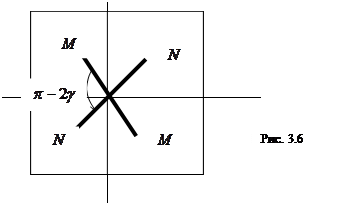
то есть свет остается линейно поляризованным, но направление колебаний изменяется на угол ( (рис. 3.6).

Помещение на пути пучка пластинки, обеспечивающей разность хода, равную

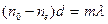, (3.10)

вносит разность фаз 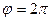или 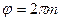, вследствие чего эллипс вырождается в прямую

,

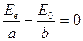то есть пучок остаётся линейно поляризованным без изменения направления колебаний.

Опишем теперь последовательность проведения анализа поляризованного света с помощью фазовых пластинок. Для полного анализа достаточно николя-анализатора и четвертьволновой фазовой пластинки.

На пути исследуемого светового пучка помещают и медленно вращают анализатор. Далее необходимо провести следующие операции, результаты которых дадут возможность сделать однозначные выводы:

1. Если интенсивность не изменяется ни в отсутствие, ни в присутствии 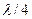-пластинки, свет естественный.

2. Если без пластинки 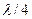интенсивность не меняется, а при наличии ее появляются максимальная и минимальная интенсивности, то свет поляризован по кругу. При этом если в минимуме интенсивность равна нулю, то свет полностью поляризован циркулярно, а если не равна нулю, то он частично циркулярно поляризован.

3. Если в отсутствие 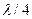-пластинки интенсивность изменяется от нуля до некоторой максимальной, свет полностью линейно поляризован.

4. Если не при этом в минимуме интенсивность не равна нулю, то возможны два случая:

а) помещение перед анализатором 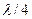-пластинки, ориентированной так, чтобы ее главные направления совпадали с азимутами максимальной и минимальной интенсивности, приводит к тому, что при вращении анализатора в некотором положении последнего, не совпадающем с азимутом прежнего минимума, интенсивность становится равной нулю. В этом случае имеем полностью эллиптически поляризованный свет;

б) если же при таком введении 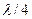-пластинки интенсивность не обращается в нуль ни при каком азимуте анализатора, то снова возможны два случая:

· введение 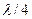-пластинки не вносит никаких изменений в азимуты анализатора, соответствующие максимуму и минимуму; это значит, что свет частично линейно поляризован;

· если же введение 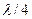-пластинки приводит к изменениям в положениях анализатора, при которых получаются максимум и минимум, то свет частично эллиптически поляризован.

Перечисленные результаты исчерпывают все возможные случаи поляризации светового пучка и поэтому в совокупности дают метод полного качественного анализа состояния поляризации.

Для количественного анализа эллиптически поляризованного света нужно знать форму и расположение эллипса эллипса, то есть разность фаз двух ортогональных компонентов любого направления. Для этой цели используют устройства, способные скомпенсировать до нуля или дополнить до 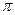любую разность фаз. Их называют компенсаторами. Примерами таких устройств являются компенсаторы Бабине и Солейля.

Сделать изучение изложенного материала наглядным и распространить представления о поляризации волн за пределы оптической области спектра могут помочь демонстрации рассмотренных выше явлений в диапазоне сантиметровых волн. Подробное их описание есть в книге Б.Ш. Перкальскиса, изданной в 1966 г. «Использование современных научных средств в физических демонстрациях». При этом фазовые пластинки и компенсаторы изготавливаются из сухой древесины (кедр, сосна, пихта).

Первое, но достаточно глубокое знакомство учащихся с поляризацией волн полезно завершить перечнем некоторых областей практического использования этого явления. Можно предложить учащимся написание рефератов о применениях поляризованного излучения в науке, технике, медицине, метеорологии, астрофизике и других областях или провести урок-конференцию «Поляризованный свет и его применения. В ходе работы над рефератом и подготовки к конференции учащиеся самостоятельно познакомятся с сутью явлений, сопровождающих прохождение поляризованного света через вещество: оптической активностью, эффектами Керра, Поккельса, Коттона-Мутона, Фарадея, с образованием коноскопических фигур при интерференции поляризованного света в кристаллах. После этого можно обсудить со школьниками ответы на вопросы, вынесенные в начало лекции. Возможно предложение учащимся тем исследовательских или технических проектов, выполнение которых требует знания свойств поляризованного света и методов поляризации света.

Литература

1. Мякишев Г.Я., Буховцев Б.Б. Физика: Учебник для 11 класса средней школы. – М.: Просвещение, 1991. – 254 с.

2. Шерклифф У. Поляризованный свет: получение и использование. – М.: Мир, 1965.- 160 с.

3. Саржевский А.М. Оптика: В 2 т. – Т. 2: Уч. пос. для физ. спец. ун-тов. – М.: Университетское, 1986. – 319 с.

4. Жевандров Н.Д. Анизотропия и оптика. – М.: Наука, 1974. – 167 с.

5. Физический энциклопедический словарь. – М.: Сов. энциклопедия, 1984. – С. 575 – 576.

6. Аззам Р., Башара Н. Эллипсометрия и поляризованный свет. – М.: Мир. – 584 с.

7. Ландсберг Г.С. Оптика. – М.: Наука, 1976. – 926 с.

8. Жевандров Н.Д. Поляризация света. – М.: Наука, 1969. – 192 с.

9. Жевандров Н.Д. Применение поляризованного света. – М.: Наука, 1978. – 176 с.