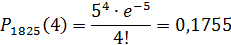Повторение независимых испытаний. Формула Бернулли
Пусть производится серия из n ‒ независимых испытаний (опытов), в каждом из которых событие A наступает с вероятностью р. Тогда вероятность того, что событие A не произойдет, обозначим: q=1 ‒ p.
Вероятность того, что при n ‒ испытаниях событие произойдет ровно m ‒ раз, находится по формуле Бернулли:
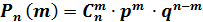
‒ формула Бернулли.
Пример.
Вероятность попадания мяча в кольцо составляет: 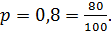
Вероятность промаха мяча в кольцо составляет 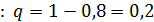
Найти:
1. Вероятность того, что при 7 бросках мяч попадет 4 раза (событие A).
2. Вероятность того, что мяч попадет не менее 4-х раз, то есть 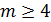 или
или 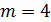 , или
, или 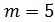 , или
, или 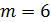 , или
, или 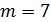 .
.
Решение:
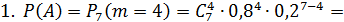

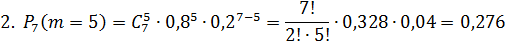
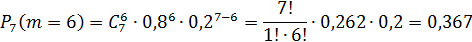
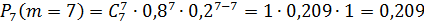
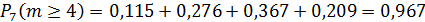
Наивероятнейшее число наступлений события (число успехов).
Определение.Число 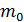 наступления события A в n ‒ независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события, по крайней мере, не меньше вероятностей других событий.
наступления события A в n ‒ независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события, по крайней мере, не меньше вероятностей других событий.
Наивероятнейшее число 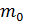 наступления события (число успехов) удовлетворяет следующему неравенству:
наступления события (число успехов) удовлетворяет следующему неравенству:
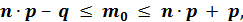
где 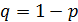 ;
; 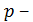 вероятность наступления события в отдельном испытании.
вероятность наступления события в отдельном испытании.
Пример.Вероятность изготовления на автоматическом станке стандартной детали 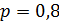 . Найти вероятности возможного числа появления бракованных деталей среди пяти отобранных и выбрать среди них наивероятнейшее число бракованных деталей.
. Найти вероятности возможного числа появления бракованных деталей среди пяти отобранных и выбрать среди них наивероятнейшее число бракованных деталей.
Решение:
1 способ.
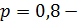 вероятность изготовления стандартной детали.
вероятность изготовления стандартной детали.
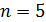 ;
; 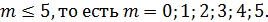
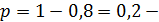 вероятность появления брака.
вероятность появления брака.
Тогда 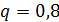
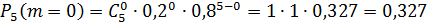
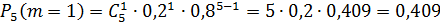
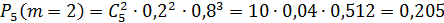
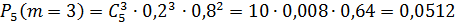
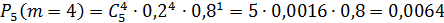
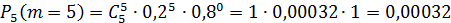
Следовательно, наивероятнейшее число бракованных деталей 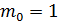 .
.
2способ.
Оценим 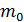 с помощью неравенства:
с помощью неравенства:
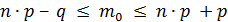
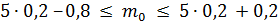
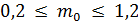
Следовательно, 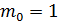 ,
, 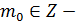 множество целых чисел.
множество целых чисел.
Приближенная формула Муавра ‒ Лапласа (локальная).
При большом значении n применение формулы Бернулли затруднительно. Тогда используют формулу Муавра‒ Лапласа. Муавр доказал частный случай для p =1/2.
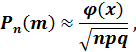
где
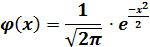
‒ функция Лапласа, значения в таблице № 1.
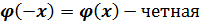
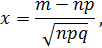
если 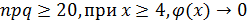 ,
, 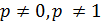
Пример.
Установлено, что 94% лиц, которым сделали прививку от туберкулеза, приобретают иммунитет. Найти вероятность того, что среди 100 000 граждан, которым делали прививки, 5800 не защищены от туберкулеза.
Решение:
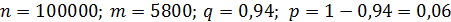
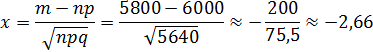
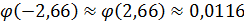
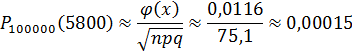
Интегральная формула Лапласа.
Если требуется найти вероятность того, что при n ‒ испытаниях событие наступит не меньше a ‒ раз и не больше b ‒ раз, то применяют интегральную формулу Лапласа:
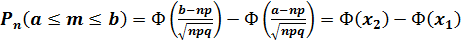 ,
,
где
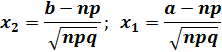
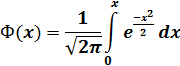
‒ интегральная функция Лапласа, значения в таблице № 2.
Ф(‒х) = ‒ Ф(x) ‒ функция нечетная.
При х 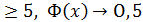
Пример.
Из каждых 100 семей 80 имеют телефоны.
Найти вероятность того, что:
1. Из каждых 400 семей 300 имеют телефоны.
2. От 300 до 360 семей из каждых 400 имеют телефоны.
3. Не менее 360 семей из 400 семей имеют телефоны ( 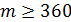 )
)
Решение:
1. 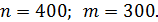
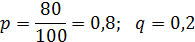
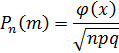
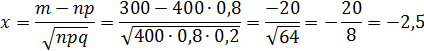
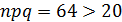
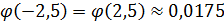
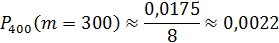
2. 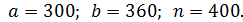
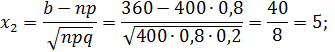
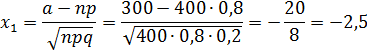
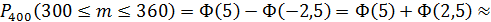
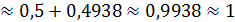
3. Так как 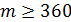 , то
, то 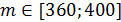
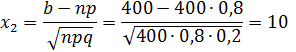
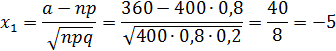
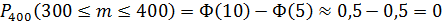
Формула Пуассона.
Если p 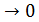 (начинается с сотых долей), то формула Муавра ‒ Лапласа дает большую погрешность по сравнению с формулой Бернулли. В этом случае пользуются формулой Пуассона:
(начинается с сотых долей), то формула Муавра ‒ Лапласа дает большую погрешность по сравнению с формулой Бернулли. В этом случае пользуются формулой Пуассона:
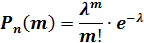
где λ= np‒ параметр Пуассона, где 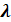 ≤ 10.
≤ 10.
Пример.
На факультете 1825 студентов. Какова вероятность, что 1-е сентября является днем рождения одновременно четырех студентов факультета?
Решение: Вероятность того, что день рождения студента 1-го сентября 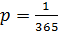 ‒ мала, n = 1825 ‒ велико, λ = np = 5 ≤ 10. Следовательно, воспользуемся формулой Пуассона:
‒ мала, n = 1825 ‒ велико, λ = np = 5 ≤ 10. Следовательно, воспользуемся формулой Пуассона: