Самостоятельная работа №6
Неопределённый интеграл
Вариант №1
1) Найти интегралы:
a)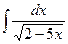 
b)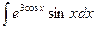 
c)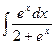 
d)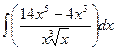 
e)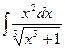 
2) Найти интегралы, используя метод интегрирования по частям:
a)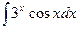 
b)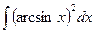 
c)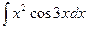 
3) Найти интегралы, используя метод неопределённых коэффициентов:
a)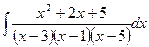 
b)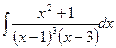 
c)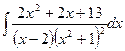 
4) Найти интегралы:
a)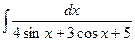 
b)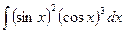 
5) Решить, используя метод Остроградского:
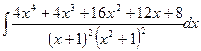
Вариант №2
1) Найти интегралы:
a)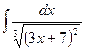 
b)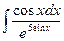 
c)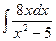 
d)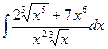 
e)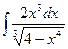 
2) Найти интегралы, используя метод интегрирования по частям:
a)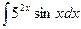 
b)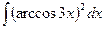 
c)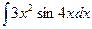 
3) Найти интегралы, используя метод неопределённых коэффициентов:
a)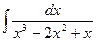 
b)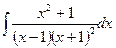 
c)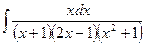 
4) Найти интегралы:
a)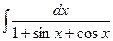 
b)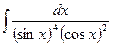 
5) Решить, используя метод Остроградского:
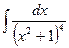
Самостоятельная работа №7
Определённый интеграл
Вариант №1
1) Вычислить определенный интеграл, рассматривая его как предел соответствующего интегрального сложения
.
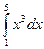2) Применяя формулу Ньютона-Лейбница, найдите интеграл: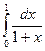 
.
3) Вычислить интегралы:
а)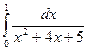 
;
б)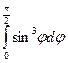 
;
в)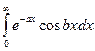 
, 
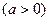
4) Вычислить несобственные интегралы (или установить их расходимость):
а)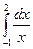 
;
б)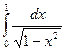 
;
в)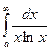 
, 
.
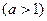5) Оценить интеграл: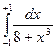 
.
6) Вычислить площадь, ограниченную параболой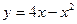 
и осью абсцисс.
Вариант №2
1) Вычислить определенный интеграл, рассматривая его как предел соответствующего интегрального сложения
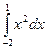
2) Применяя формулу Ньютона-Лейбница, найдите интеграл: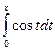 
.
3) Вычислить интегралы:
а)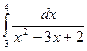 
;
б)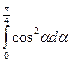 
;
в)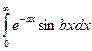 
, .
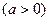4) Вычислить несобственные интегралы ( или установить их расходимость ):
а)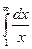 
;
б)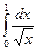 
;
в)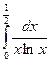 
.
5) Оценить интеграл: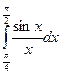 
.
6) Вычислить площадь, ограниченную параболой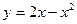 
и прямой 
.
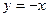ФОНД ОЦЕНОЧНЫХ СРЕДСТВ ДЛЯ ПРОВЕДЕНИЯ ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ОБУЧАЮЩИХСЯ ПО ДИСЦИПЛИНЕ
ТЕХНОЛОГИЧЕСКАЯ КАРТА ДИСЦИПЛИНЫ
ТЕХНОЛОГИЧЕСКАЯ КАРТА
по дисциплине
Математический анализ
для студентов I курса направления “Экономика”
2 семестр
Максимальное количество баллов по дисциплине - 100:
- 26 баллов - посещаемость и активное участие на практических занятиях;
- 20 баллов - выполнение контрольных заданий;
- 20 баллов - итоговое тестирование;
- 34 балла - самостоятельная работа студента.
Всего практических занятий 52 часа (26 занятий).
Система оценивания
Практические занятия
- посещение занятия оценивается в 0,5 баллов;
- активное участие – 0,5 баллов.
Контрольные работы
Контрольная работа №1 по темам: «Пределы последовательностей и функций. Числовые и степенные ряды»;
Контрольная работа №2 по темам: «Производная функции одной переменной. Исследование функции».
Каждая контрольная работа оценивается в 10 баллов.
Задания для самостоятельной работы приведены в рабочей программе курса и доступны в локальной сети НФ БашГУ. Для оценивания студенты сдают отчет по самостоятельной работе (составляют в тетради конспекты по темам, отведенным для самостоятельного изучения; выполняют задания по самостоятельной работе (домашние задания)).
Форма отчетности по самостоятельной работе
Защита самостоятельной работы проводится по графику консультаций и графику КСР преподавателя.