Как выглядит эпюра касательных напряжений для балки круглого поперечного сечения?
Прежде чем ответить на этот вопрос, попробуем сначала выяснить, какое вообще направление имеет касательное напряжение, возникающее в некоторой точке контура поперечного сечения стержня.
Рассмотрим поперечное сечение стержня, имеющее совершенно произвольную форму (рис. 7.13, а). Предположим, что в некоторой точке К его контура возникает касательное напряжение 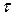 , направленное под каким-то углом по отношению к контуру. Разложим это напряжение на две составляющие:
, направленное под каким-то углом по отношению к контуру. Разложим это напряжение на две составляющие: 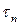 – по нормали и
– по нормали и 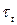 – по касательной к контуру сечения. Если напряжение
– по касательной к контуру сечения. Если напряжение 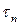 действительно существует, то по закону парности касательных напряжений на поверхности стержня должно существовать и равное ему по значению касательное напряжение
действительно существует, то по закону парности касательных напряжений на поверхности стержня должно существовать и равное ему по значению касательное напряжение 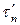 . Но поверхность стержня при изгибе не нагружена внешними силами, параллельными оси балки z. Поэтому касательное напряжение на поверхности стержня
. Но поверхность стержня при изгибе не нагружена внешними силами, параллельными оси балки z. Поэтому касательное напряжение на поверхности стержня 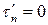 и, следовательно,
и, следовательно, 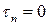 .
.
Таким образом, при изгибе балки касательное напряжение, возникающее в некоторой точке контура поперечного сечения, всегда направлено по касательной к контуру.
Покажем, что в вершине угла прямоугольного поперечного сечения балки касательное напряжение при изгибе равно нулю (рис. 7.13, б).
Предположим, что в вершине угла, в точке M,возникает некоторое касательное напряжение 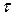 . Разложим его на составляющие
. Разложим его на составляющие 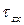 и
и 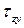 . Но касательные напряжения на поверхности балки отсутствуют (
. Но касательные напряжения на поверхности балки отсутствуют ( 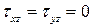 ). Поэтому по закону парности касательных напряжений должны быть равны
). Поэтому по закону парности касательных напряжений должны быть равны 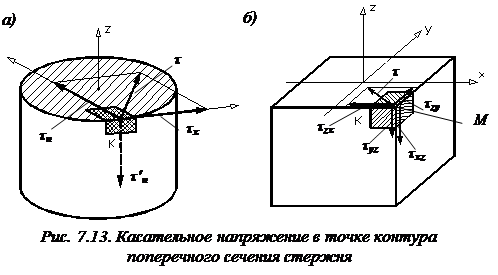
нулю и составляющие 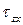 и
и 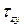 . Следовательно, в точке M
. Следовательно, в точке M 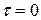 .
.
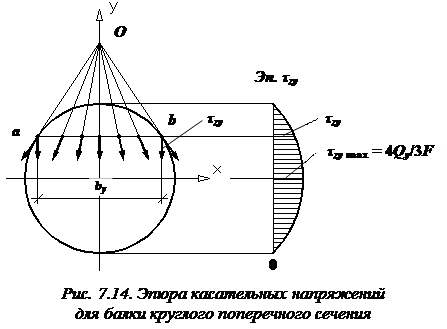
С учетом изложенного выше, задача вычисления касательных напряжений в произвольной точке балки круглого поперечного сечения заметно усложняется. Однако, если сделать предположение о том, что в точках, расположенных на некоторой линии ab (рис. 7.14), касательные напряжения 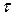 направлены так, что все они пересекаются в точке О, и дополнительно предположить, что вертикальные проекции этих напряжений равномерно распределены вдоль линии ab, то формулу Журавского можно использовать для вычисления вертикальных проекций
направлены так, что все они пересекаются в точке О, и дополнительно предположить, что вертикальные проекции этих напряжений равномерно распределены вдоль линии ab, то формулу Журавского можно использовать для вычисления вертикальных проекций 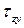 . Вычисление всех остальных величин, входящих в формулу (7.8), производится так же, как и, например, для прямоугольного поперечного сечения.
. Вычисление всех остальных величин, входящих в формулу (7.8), производится так же, как и, например, для прямоугольного поперечного сечения.
В частности, наибольшие касательные напряжения, возникающие в точках, расположенных на нейтральной оси x, вычисляются по формуле
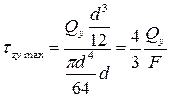 .
.
7.32. Согласно гипотезе Бернулли считается, что при изгибе балки ее продольные волокна не оказывают давления друг на друга. Такое предположение для чистого изгиба вполне естественно. Но насколько это допущение справедливо при поперечном изгибе балки?
Рассмотрим, например, жестко защемленную балку прямоугольного поперечного сечения, нагруженную сверху равномерно распределенной поперечной нагрузкой q. Тогда в точках, принадлежащих верхним волокнам балки, возникнут нормальные напряжения:
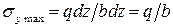 .
.
В нижних же волокнах, ввиду отсутствия поверхностной нагрузки, 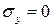 . При существующих на практике значениях внешней нагрузки напряжение
. При существующих на практике значениях внешней нагрузки напряжение 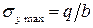 настолько мало по сравнению с наибольшим нормальным напряжением
настолько мало по сравнению с наибольшим нормальным напряжением 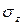 , возникающем в поперечном сечении балки, что им можно пренебречь. Покажем это.
, возникающем в поперечном сечении балки, что им можно пренебречь. Покажем это.
Для рассматриваемой балки наибольший изгибающий момент возникает в заделке. Он равен 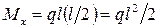 . В этом случае
. В этом случае
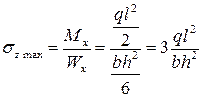 .
.
Тогда 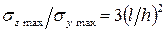 . Для реальных балок отношение
. Для реальных балок отношение 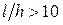 , поэтому окончательно получим:
, поэтому окончательно получим:
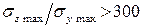 .
.
7.33. Как проверяется прочность балки при изгибе и как подбираются размеры ее поперечного сечения?
Проверка прочности балки осуществляется, как правило, только по наибольшим нормальным напряжениям. Эти напряжения, как мы уже знаем, возникают в крайних волокнах того поперечного сечения балки, в котором «действует» наибольший по абсолютному значению изгибающий момент 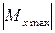 . Его значение мы определяем по эпюре изгибающих моментов.
. Его значение мы определяем по эпюре изгибающих моментов.
При поперечном изгибе в балке наряду с нормальными напряжениями возникают и касательные напряжения, но они в подавляющем числе случаев невелики и при расчете на прочность учитываются, в основном, только для балок двутаврового профиля, о чем мы будем говорить особо.
Условие прочности балки при изгибе по нормальным напряжениям имеет вид:
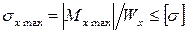 , (7.10)
, (7.10)
где допускаемое напряжение 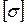 принимается таким же, как и при растяжении (сжатии) стержня из такого же материала.
принимается таким же, как и при растяжении (сжатии) стержня из такого же материала.
Помимо проверки прочности, по формуле (7.10) может быть произведен и подбор размеров поперечного сечения балки. При заданном допускаемом напряжении 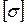 и известном максимальном абсолютном значении изгибающего момента
и известном максимальном абсолютном значении изгибающего момента 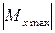 требуемый момент сопротивления балки при изгибе определяется из следующего неравенства:
требуемый момент сопротивления балки при изгибе определяется из следующего неравенства:
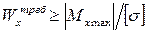 .
.
Необходимо иметь в виду следующее очень важное обстоятельство. При изменении положения поперечного сечения балки по отношению к действующей нагрузке ее прочность может существенно изменится, хотя площадь поперечного сечения F и останется прежней.
Пусть, например, балка прямоугольного поперечного сечения с отношением сторон 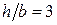 расположена по отношению к силовой плоскости таким образом, что ее высота h перпендикулярна к нейтральной оси x. В этом случае отношение моментов сопротивления балки при изгибе равно:
расположена по отношению к силовой плоскости таким образом, что ее высота h перпендикулярна к нейтральной оси x. В этом случае отношение моментов сопротивления балки при изгибе равно:
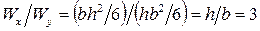 .
.
То есть такая балка в три раза прочнее той же самой балки, но повернутой на 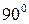 .
.
Напомним, что в выражении для момента сопротивления балки прямоугольного поперечного сечения при изгибе в квадрате стоит тот ее размер, который перпендикулярен нейтральной оси.
Следовательно, сечение балки необходимо располагать таким образом, чтобы силовая плоскость совпадала с той из главных центральных осей, относительно которой момент инерции минимален. Или, что то же самое, необходимо добиваться того, чтобы нейтральной осью являлась ось, относительно которой главный момент инерции поперечного сечения максимален. В этом случае говорят, что балка испытывает изгиб в плоскости наибольшей жесткости.
Сказанное выше еще раз подчеркивает важность темы «Определение положения главных центральных осей инерции поперечного сечения стержня», к которой студенты относятся, как правило, поверхностно.
Определив из условия прочности (7.10) требуемый момент сопротивления при изгибе 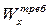 , мы можем перейти к определению размеров и формы поперечного сечения балки. При этом нам необходимо стремиться к тому, чтобы вес балки оказался минимальным.
, мы можем перейти к определению размеров и формы поперечного сечения балки. При этом нам необходимо стремиться к тому, чтобы вес балки оказался минимальным.
При заданной длине балки ее вес пропорционален площади поперечного сечения F.
Покажем, например, что квадратное поперечное сечение является более экономным, чем круглое.
В случае квадратного поперечного сечения, как мы знаем, момент сопротивления при изгибе определяется по формуле
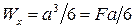 .
.
Для круглого поперечного сечения он равен:
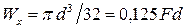 .
.
Если предположить, что площади поперечных сечений квадрата и круга равны между собой, то сторона квадрата a может быть выражена через диаметр круга d:
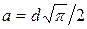 .
.
Тогда момент сопротивления балки квадратного поперечного сечения будет равен:
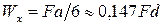 .
.
Сравнивая полученное значение момента сопротивления с моментом сопротивления балки круглого поперечного сечения 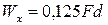 , приходим к выводу, что квадратное поперечное сечение при той же площади имеет больший момент сопротивления, чем круглое (почти на 18 %). Следовательно, квадратное поперечное сечение является более экономичным по сравнению с круглым.
, приходим к выводу, что квадратное поперечное сечение при той же площади имеет больший момент сопротивления, чем круглое (почти на 18 %). Следовательно, квадратное поперечное сечение является более экономичным по сравнению с круглым.
Анализируя распределение нормальных напряжений по высоте поперечного сечения балки (см. формулу (7.5)), легко прийти к заключению, что та часть материала, которая расположена вблизи нейтральной оси, почти не «работает» (это, в частности, и указывает на нерациональность круглого поперечного сечения по сравнению с квадратом). Для получения наибольшей экономии материала его нужно поместить как можно дальше от нейтральной оси. Наиболее благоприятный случай при заданной площади поперечного сечения F и высоте h получится при расположении каждой половины площади на расстоянии 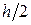 от нейтральной оси. Тогда момент инерции и момент сопротивления будут соответственно равны:
от нейтральной оси. Тогда момент инерции и момент сопротивления будут соответственно равны:
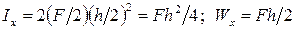 .
.
Это тот предел, к которому можно приблизиться, применяя двутавровое поперечное сечение с наибольшим количеством материала в полках.
Однако, вследствие необходимости выделить часть материала для стенки балки, полученное предельное значение для момента сопротивления недостижимо. Так, для прокатных балок двутаврового профиля:
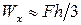 .
.
Для таких балок проверка прочности производится следующим
образом:
· в точках наиболее удаленных от нейтральной оси прочность двутавровой балки проверяется по формуле (7.10);
· в точках, где полка соединяется со стенкой, то есть в тех точках, где велики и нормальные, и касательные напряжения, – по главным напряжениям:
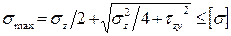 ,
,
или же применяется одна из формул гипотез прочности (см. далее беседу 8);
· в точках, расположенных на нейтральной оси, – по наибольшим касательным напряжениям:
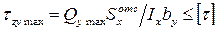 .
.
7.34. Чему равна потенциальная энергия деформации при изгибе?
Потенциальная энергия деформации балки при поперечном изгибе определяется по следующей формуле (подробнее см. беседу 15)
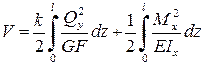 , (7.11)
, (7.11)
где первый интеграл представляет собой потенциальную энергию сдвига, а второй – энергию чистого изгиба.
Значение безразмерного коэффициента k, входящего в первое слагаемое выражения (7.11), зависит от формы поперечного сечения балки и вычисляется по формуле
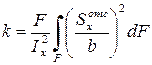 .
.
Например, для прямоугольного поперечного сечения 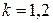 .
.
Для большинства типов балок первое слагаемое в формуле (7.11) значительно меньше второго слагаемого. Поэтому при определении потенциальной энергии деформации при изгибе влиянием сдвига (первым слагаемым) часто пренебрегают.
7.35. С какой целью определяются перемещения балки при
изгибе?
Для того чтобы судить о работе балок, недостаточно иметь информацию только о напряжениях, которые возникают в ней при деформировании. Весьма прочные балки могут оказаться непригодными к эксплуатации из-за недостаточной их жесткости. Если балка сильно прогибается под нагрузкой, то в ней могут возникнуть изгибные колебания с большими амплитудами, приводящие к дополнительным напряжениям.
Для проверки жесткости балки необходимо уметь определять перемещения отдельных точек ее оси.
В результате изгиба ось балки становится криволинейной. Изогнутую ось балки принято называть упругой линией балки.Кривизна упругой линии балки может быть определена из формулы (7.4):
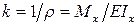 .
.
Напомним, что вертикальное перемещение произвольной точки, лежащей на оси балки, при изгибе (прогиб балки) обозначается буквой v, продольное перемещение – буквой u, а угол поворота поперечного сечения балки– буквой 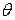 .
.
Проверка жесткости балки сводится к требованию, согласно которому ее наибольший прогиб 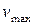 , называемый стрелой прогиба, не должен превышать определенной доли от пролета балки l:
, называемый стрелой прогиба, не должен превышать определенной доли от пролета балки l:
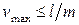 .
.
Здесь число m устанавливается нормами проектирования и колеблется обычно в пределах от 300 до 1000. Для ответственных сооружений, например, для мостов, 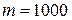 . Отсюда видно, что прогибы балки при изгибе малы по сравнению с ее пролетом. Это позволяет нам в дальнейшем изложении ввести следующие упрощения:
. Отсюда видно, что прогибы балки при изгибе малы по сравнению с ее пролетом. Это позволяет нам в дальнейшем изложении ввести следующие упрощения:
· во-первых, при малых прогибах v угол наклона касательной к изогнутой оси балки и, следовательно, угол поворота поперечного сечения балки можно определять с помощью выражения
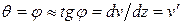 ;
;
· во-вторых, горизонтальным перемещением u можно пренебречь, так как оно по сравнению с прогибом v и углом поворота поперечного сечения 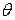 является величиной более высокого порядка малости.
является величиной более высокого порядка малости.
В результате мы можем считать, что угол поворота поперечного сечения равен первой производной от прогиба балки и что каждая точка оси балки перемещается только по вертикали.
Следовательно, для определения полной картины деформации нам необходимо получить уравнение упругой линии балки 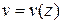 .Если эта функция известна, то, определив прогибы балки в ряде точек, можно построить кривую прогибов и найти наибольший прогиб, который и позволит нам судить о жесткости балки.
.Если эта функция известна, то, определив прогибы балки в ряде точек, можно построить кривую прогибов и найти наибольший прогиб, который и позволит нам судить о жесткости балки.
В заключение отметим, что в ряде задач, главным образом статически неопределимых, возникает необходимость и в определении угла поворота поперечного сечения балки.
7.36. Как записывается дифференциальное уравнение изгиба балки?
Для определения уравнения изогнутой оси балки можно воспользоваться законом Гука (7.4):
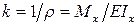 .
.
Из курса высшей математики нам известно следующее выражение для кривизны некоторой кривой:
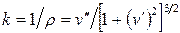 .
.
В пределах упругих деформаций квадрат угла поворота поперечного сечения балки ничтожно мал по сравнению с единицей. Поэтому 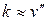 , то есть вторая производная от прогиба представляет собой кривизну изогнутой оси балки в рассматриваемом месте. Тогда
, то есть вторая производная от прогиба представляет собой кривизну изогнутой оси балки в рассматриваемом месте. Тогда
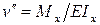 .
.
Это дифференциальное уравнение описывает изгиб балки в рамках гипотезы Бернулли. Продифференцировав его дважды по z, с учетом третьей формулы (7.1), получим:
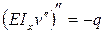 .
.
Для балки постоянной жесткости ( 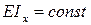 ) будем иметь
) будем иметь
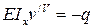 . (7.12)
. (7.12)
Дифференциальное уравнение четвертого порядка (7.12) называется дифференциальным уравнением изгиба балки.
Интегрируя уравнение (7.12) первый раз, получим выражение, дающее закон изменения перерезывающей силы по длине балки. Второе интегрирование определяет характер изменения изгибающего момента, третье интегрирование – углов поворота поперечных сечений, наконец, четвертое – прогибов балки по ее длине. При этом четыре постоянные интегрирования определяются из условий опирания балки.
7.37. Как на практике осуществляется вычисление прогибов и углов поворота поперечных сечений балки?
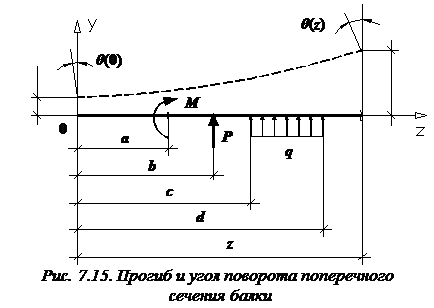
Они могут быть определены, например, с помощью так называемого универсального уравнения упругой линии балки. Мы приведем это уравнение без вывода. Прогиб балки в сечении с координатой z и угол поворота этого же сечения (рис. 7.15) определяются по следующим формулам:
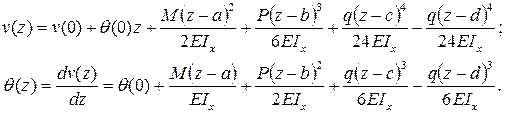 (7.13)
(7.13)
Здесь a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.
Заметим, что в формулы (7.13) входят только те внешние усилия (активные и реактивные), которые расположены левее сечения, в котором определяются перемещения балки.
Если какая-нибудь нагрузка (нагрузки) имеют направление, противоположное тому, что указано на рис. 7.15, то у соответствующего слагаемого (слагаемых) в формулах (7.13) следует поменять знак на противоположный. В случае многократного повторения однотипных нагрузок необходимо использовать суммирование соответствующих слагаемых.

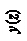
Прогиб 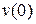 и угол поворота
и угол поворота 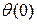 балки в начале координат (начальные параметры) определяются из условий закрепления балки.
балки в начале координат (начальные параметры) определяются из условий закрепления балки.
Продемонстрируем использование формул (7.13) на примере балки (см. рис. 7.4). Определим, например, прогиб балки на консоли при 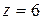 м, то есть
м, то есть 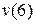 . Запишем универсальное уравнение упругой линии балки:
. Запишем универсальное уравнение упругой линии балки:
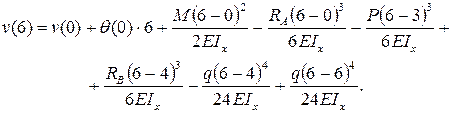
Очевидно, что прогиб балки в начале координат (на левой шарнирной опоре) равен нулю. То есть 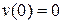 .
.
Для определения угла поворота в начале координат 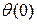 необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.
необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.
Таким образом, будем иметь:
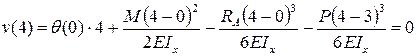 ,
,
отсюда
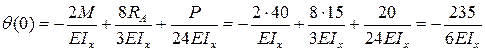 .
.
Тогда окончательно прогиб консоли равен:
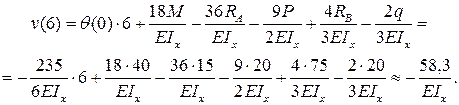
Знак «минус» говорит нам о том, что прогиб балки на консоли происходит вниз. Отметим также, что число, стоящее в числителе, измеряется в нашем примере в килоньютонах на метр в кубе (кН·м3).
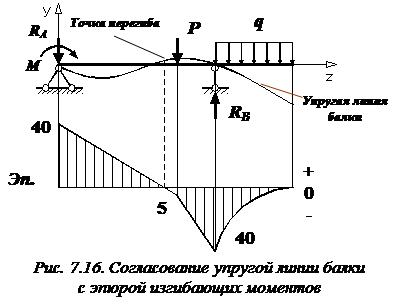 |
Примерный вид упругой линии балки показан на рис. 7.16.
Упругая линия балки должна быть согласована с эпюрой изгибающих моментов. Напомним, что положительный изгибающий момент «изгибает» балку выпуклостью вниз (сжатые волокна сверху), а отрицательный – выпуклостью вверх (сжатые волокна снизу). Точка перегиба, то есть та точка, в которой кривизна балки равна нулю, находится под тем сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука.
