Модель двойственной задачи построенной к данной
f = 8х1 - 4х2+ 7х3 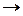 max.
max.
 2х1+ 3х2 - 4х3
2х1+ 3х2 - 4х3 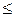 106,
106,
5х1+ 4 х2 + х3 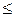 205,
205,
4х1+ 2х2+ 8х3 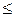 340.
340.
хj 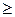 0, (j=
0, (j= 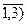 .
.
принимает следующий вид:
1) φ = 8 у1 – 4 у2 + 7 у3 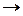 min min 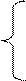 2у1 + 3 у2 – 4у3 2у1 + 3 у2 – 4у3 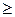 106 5у1 +4 у2 + у3 106 5у1 +4 у2 + у3 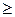 205 4у1 + 2у2 + 8у3 205 4у1 + 2у2 + 8у3 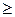 340 уi 340 уi 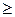 0, I = 0, I = 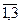 | 2) φ = 106 у1 + 205 у2 +340 у3  min min  2у1 + 5 у2 + 4у3 2у1 + 5 у2 + 4у3 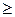 8 3у1 +4 у2 + 2 у3 8 3у1 +4 у2 + 2 у3 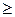 -4 -4у1 + у2 + 8у3 -4 -4у1 + у2 + 8у3 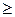 7 уi 7 уi 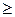 0, i = 0, i = 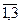 |
3) φ = 106 у1 + 205 у2 +340 у3  max (ДА) max (ДА) 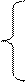 2у1 + 5 у2 + 4у3 2у1 + 5 у2 + 4у3 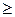 8 3у1 +4 у2 + 2 у3 8 3у1 +4 у2 + 2 у3 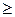 -4 -4у1 + у2 + 8у3 -4 -4у1 + у2 + 8у3 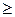 7 уi 7 уi 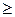 0, I = 0, I = 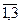 | 4) φ = 8 у1 - 4 у2 + 7 у3 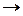 max max  2у1 + 3 у2 - 4у3 2у1 + 3 у2 - 4у3 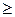 106 5у1 +4 у2 + у3 106 5у1 +4 у2 + у3 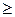 205 4у1 + 2у2 + 8у3 205 4у1 + 2у2 + 8у3 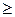 340 уi 340 уi 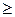 0, i = 0, i = 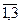 |
Матрица строки и столбцы которой соответствуют вершинам и ребрам графа, а элементы 1 или 0 в зависимости от наличия связи между вершинами и ребрами:
Инцидентностей
Метод Парето:
сокращает область поиска компромиссных решений многокритериальной оптимизации
Метод при котором для нахождения начального опорного плана записывается число в первую клетку:
а) метод Фогеля
б) метод северо-западного угла (ДА)
в) метод потенциалов
г) метод наименьшего элемента
Между переменными прямой и двойственной задачи можно:
а) установить взаимно однозначное соответствие;
б) произвести замену переменных;
в) установить регрессионную зависимость между переменными;
г) привести подобные члены.
Множители Лагранжа λi (i=1,m) показывают:
на сколько изменится значение функции в оптимальном решении при изменении правой части i-го ограничения на единицу:
Модель транспортной задачи это:
а) модель задачи линейной оптимизации;
б) модель сетевого планирования
в) модель динамического программирования или это.
Модифицированные жордановы исключения применяются для нахождения:
а) обратной матрицы;
б) ранга матрицы;
в) решений систем линейных уравнений;
г) решения задач оптимизации;
д) всего перечисленного в пунктах а), б), в) и г).
Начальный опорный план транспортной задачи ищется методом:
Северо-западного угла
Фогеля
Начальный опорный план транспортной задачи можно составить:
а) методом Жордана;
б) методом минимальной стоимости;
в) методом аппроксимации;
г) методом Фогеля;
д) применяя методы пунктов б) и г).
Найдите верные утверждения применительно к задаче рационального использования ограниченных ресурсов:
а) двойственные оценки в оптимальном решении задачи характеризуют дефицитность ресурсов;
б) ресурс, полностью использованный в оптимальном решении, является дефицитным, его двойственная оценка — больше нуля;
в) если ресурс расходован не полностью, то он избыточен, его двойственная оценка равна нулю;
г) если ресурс расходуется не полностью, то он избыточен, его двойственная оценка больше нуля.
На рисунке изображен случай, когда своего максимального значения функция f(х) достигает
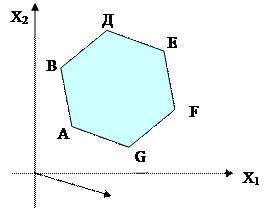 | 1) в точке Е; 2) в точке В; 3) в точке А; 4) на отрезке ВД; 5) в точке F |
Найдите правильное преобразование неравенства 11Х1 + 3Х2 > -19
-11Х1 – 3Х2 < 19
Область допустимых решений задачи линейной оптимизации:
а) может быть объединением двух выпуклых многоугольников НЕТ
б) может быть окружностью
в) может образовывать невыпуклый многоугольник с отрицательными координатами вершин.
г) может быть пустым множеством (ДА)
Область допустимых решений задачи линейной оптимизации:
а) может быть пустым множеством;
б) не может быть пустым множеством;
в) может быть точкой;
г) может быть отрезком прямой;
д) может быть окружностью;
е) может образовывать выпуклый многоугольник (в пространстве — многогранник).
Область допустимых решений задачи нелинейного программирования может быть:
а) выпуклой
б) вогнутой
в) из нескольких частей
г) выпуклой, вогнутой и состоять из нескольких частей
Основным принципом, на котором базируется оптимизация в задачах динамического программирования, является:
а) принцип оптимальности Р. Беллмана;
б) принцип особенностей вычислительного метода;
в) принцип планового соответствия переменных;
г) принцип дуализма.
