Оценка погрешностей методов

Полученные формулы интегрирования обычно дают приближенный результат. Можно показать [1]–[3], что абсолютная погрешность при вычислении интеграла (3.1) методами правых, левых и средних прямоугольников, трапеций и Симпсона удовлетворяет неравенствам:

(3.10)

(3.11)

(3.12)

(3.13)

(3.14)

где

(3.15)

В ряде случаев получить оценки и оказывается сложным. Тогда их удобнее выразить через конечные разности :

(3.16)

где

(3.17)

С учетом этого неравенства (3.10)–(3.14) примут вид:

(3.18)

(3.19)

(3.20)

(3.21)

(3.22)

Из условий (3.10)–(3.14) следуют ограничения на выбор величины шага h или на число отрезков интегрирования n. В частности,

(3.23)

(3.24)

(3.25)

(3.26)

При этом n должно быть целым, а для метода Симпсона еще и четным.

Проверить, достигнута ли требуемая точность метода, и заодно определить необходимую величину шага можно по методу Рунге, который заключается в следующем. Выполняются два вычисления значения интеграла – одно с выбранным шагом h, другое – с шагом h/2. Если выполняется неравенство

(3.27)

где для формул средних прямоугольников и трапеций, для формулы Симпсона, то результат вычисления дает приближенное значение интеграла с требуемой точностью 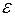. Если неравенство (3.27) не выполняется, то начальный шаг интегрирования нужно уменьшить в два раза и опять повторить вычисления. Практически для оценки точности вычислений можно пользоваться правилом: совпадающие десятичные знаки у значений интеграла, вычисленные с h и h/2, принадлежат точному значению интеграла.

Полная погрешность вычисления интеграла складывается из суммы погрешности округлений (где – максимальная ошибка округления значений подынтегральной функции) и погрешности метода.

Задание на лабораторную работу

1. Из табл. 3.1 выбрать свой вариант задания.

Таблица 3.1

Варианты заданий

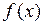№		a	b	№		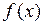a	b
		0,2	0,44			0,5	1,3
		0,3	0,7			0,1	0,9
		0,5	1,7			0,5	1,3
		0,6	1,8			0,2	1,0
		3,0	4,6			0,1	0,9
		1,7	2,9			0,2	1,0
		2,0	2,8				15,2
		1,7	2,5				6,2
		0,4	1,2			0,1	0,9
		0,1	0,9			0,1	0,9
		0,4	1,2			40,0	42,4
		0,4	1,2			0,2	1,0
		0,4	1,2			0,3	1,1
		0,2	1,0			0,1	0,9
		0,3	1,1			0,8	1,2

2. Составить таблицу значений функции и конечных разностей, предварительно разбив отрезок интегрирования на 8 частей.

3. Вычислить на микрокалькуляторе значение определенного интеграла по формулам трапеций и Симпсона. Провести оценку погрешности полученных значений интеграла. Сравнить результаты.

4. Продолжить работу в компьютерном классе.

5. Выписать точное значение интеграла и найти абсолютные погрешности найденных с помощью калькулятора значений методами трапеций и Симпсона.

6. Выписать, полученные на компьютере число точек разбиения n отрезка интегрирования 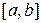, обеспечивающее точность методов левых и правых прямоугольников и значения интеграла при этих значениях n.

7. Выписать, полученные на компьютере число точек разбиения n отрезка интегрирования 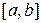, обеспечивающее точность методов средних прямоугольников, трапеций и Симпсона и значения интеграла при этих значениях n.

8. Используя полученные данные, оформить отчет по работе, в который входят: титульный лист; таблица значений функции и конечных разностей; значения интеграла и погрешности методов трапеций и Симпсона для n=8; полученное с помощью компьютера точное значение интеграла; вычисленные на МК абсолютные погрешности найденных значений интеграла; найденное на ЭВМ число точек разбиения, обеспечивающее точность методов правых и левых прямоугольников; число точек разбиения, обеспечивающее точность методов средних прямоугольников, трапеций и Симпсона; значения интегралов этих методов и их абсолютные погрешности.