Приоритетная задача линейного программирования
Приоритетная задача состоит в том, что в рамках заданных ограничений дополнительного оговаривается порядок выполнения данных ограничений. Возвращаясь к нашему примеру раскроя материала, где заданы ограничения - не менее 80 деталей первого типа и не менее 40, может быть дополнительно введено, например, следующее ограничение - в первую очередь, необходимо произвести не мерее 30 деталей первого типа и не менее 20-второго, во вторую очередь……. – и т.д., т.е. вводится некоторый приоритет на очередность решаемых задач. При такой постановке задачи уже действительно можно говорить об оптимальном планировании, т.к. учитывается собственно последовательность выполнения работ.
При использовании классических методов решении задач линейного программирования (СМ), не позволяющих учитывать динамику плана, данная задача разбивается на соответствующую совокупность не взаимосвязанных задач ЛП – число задач определяется числом приоритетов.
Векторный метод решения задач ЛП позволяет строить оптимальные планы с учетом динамики выполнения работ. Рассмотрим, как решается приоритетная задача линейного программирования векторным методом, и, в первую очередь, как она интерпретируется.
В общем случае приоритетная задача линейного программирования в своей формальной постановке выглядит следующим образом: пусть задано I приоритетов на заданную область ограничений. Соответственно имеем следующую систему ограничений: 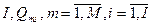 . При этом задается, что в I-ю очередь требуется выполнить
. При этом задается, что в I-ю очередь требуется выполнить 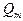 ограничений. Постановка задачи имеет вид: найти
ограничений. Постановка задачи имеет вид: найти 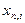 , такие, что
, такие, что 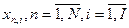 . Обращается в минимум целевая функция:
. Обращается в минимум целевая функция: 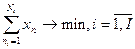 При условии, что:
При условии, что: 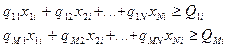 . При чем:
. При чем: 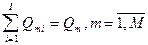 .
.
 Векторная интерпретация задачи состоит в следующем (см. рис.). На плоскости появляется система допустимых областей решений. Допустимая область с меньшим порядковым номером более приоритетна, данные ограничения должны выполняться в первую очередь. В каждой допустимой области должен быть отложен идеальный вектор из начала координат в первую область и из вершины предыдущей области в начало координат во второй области. Далее задача может решаться так же как и в случае без приоритетной постановке, путем выбора лучшего вектора на каждом этапе. Однако существуют два правила преодоления области допустимых решений.
Векторная интерпретация задачи состоит в следующем (см. рис.). На плоскости появляется система допустимых областей решений. Допустимая область с меньшим порядковым номером более приоритетна, данные ограничения должны выполняться в первую очередь. В каждой допустимой области должен быть отложен идеальный вектор из начала координат в первую область и из вершины предыдущей области в начало координат во второй области. Далее задача может решаться так же как и в случае без приоритетной постановке, путем выбора лучшего вектора на каждом этапе. Однако существуют два правила преодоления области допустимых решений.
Таким образом, данный подход позволяет использовать возможности векторной интерпретации (возможность поиска не только лучших решений в плане, но и их очередность) для решения приоритетных задач, отличающихся своей постановкой - заданием очередности выполнения ограничений.
