Алгоритм для получения одной реализации дискретной случайной величины, распределенной по рекуррентной формуле

Введение

Метод Монте-Карло – это метод, использующий случайные числа для решения разнообразных задач. Случайные числа можно получать с помощью рулетки, что собственно и делают постоянно в игорных заведениях города Монте-Карло (княжество Монако). Так возникло название метода, а развитие метод получил в первую очередь в связи с расчетами атомной бомбы и ядерных реакторов.

Развитию методов Монте-Карло способствует бурное развитие ЭВМ. Алгоритмы Монте-Карло легко программируются и позволяют рассчитывать многие задачи, недоступные для классических численных методов.

Решать методами Монте-Карло можно любые математические задачи, а не только задачи, связанные со случайными величинами.

Среди методов Монте-Карло можно выделить методы, в которых полностью воспроизводится модель рассчитываемого процесса. Такие методы называют имитационные.

Часть I. Моделирование случайных величин

Метод Монте-Карло можно определить как метод моделирования случайных величин с целью вычисления характеристик их распределений. Обычно это математические ожидания рассматриваемых случайных величин и их дисперсии.

Моделирование дискретной случайной величины

Дискретная случайная величина задаётся таблицей распределения

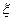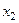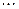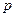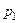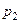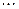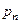Таблица 1.1

где

. (1.1)

Разобьём интервал на интервалы 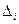такие, что дли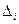на равна 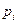. Пусть 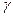– случайная величина равномерно распределённая на .

Теорема 1.1. Случайная величина 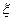, определённая формулой 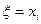, когда значение 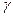принадлежит 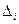, имеет распределение вероятностей, представленное таблицей 1.1.

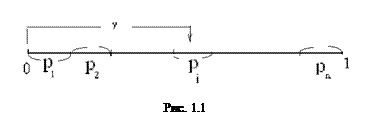
Доказательство основано на следующем соотношении (см. рис.1.1):

.

Алгоритм для получения одной реализации дискретной случайной величины, распределенной по табл. 1.1

1. Полагаем .
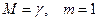2. Находим .
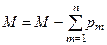3. Проверяем .
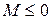4. Если 3) выполняется, то полагаем и идём в пункт 5). В противном случае полагаем 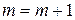и идём в пункт 2).
5. Конец.

Наиболее часто используются целочисленные случайные величины с распределением

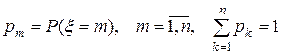. (1.2)

Пример 1.1. Требуется разыграть два возможных значения дискретной случайной величины 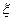, закон распределения которой задан следующей таблицей

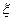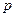	0.22	0.31	0.47

Разобьём интервал (0,1) на три интервала

, , .

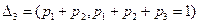Для нашего примера это следующие интервалы:

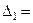(0,0.22), (0.22,0.53), 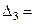(0.53, 1).

Считаем, что в нашем распоряжении имеется способ получения независимых реализаций равномерно распределённой на промежутке (0,1) случайной величины .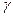

Независимые реализации случайной величины 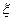будем получать следующим образом.

Пусть 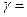0.61. Так как 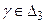, то 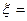3. Если 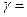0.19, то 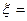1, так как в данном случае и т.д..

Алгоритм для получения одной реализации дискретной случайной величины, распределенной по рекуррентной формуле

Упражнение 1.1. Для дискретного распределения Пуассона

,

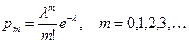с параметром 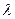необходимо получить ряд значений .

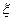Алгоритм.

Замечание. При моделировании следует учесть то, что вероятности подчиняются рекуррентным формулам

.
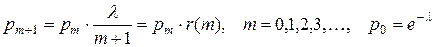