Арктангенс, арккотангенс

Определение: (арктангенс а) - это такое число из интервала , тангенс которого равен а.

Определение: (арккотангенс а) - это такое число из интервала (0; π), котангенс которого равен а.

Свойства:

1.

2.

Упражнения:

1. Вычислить:

1) = ________

2) = ___

3) = ________

4) = _______

5) = ____

6) = _______

7) = _______________________

__________________

8) = ________________________

__________________

9) =_________________________

___________________

10) = ____________________

__________________

11) = ___________________________

__________________

12) = _

___________________

13) =_____________________________

___________________

2. Решить неравенства:

1) ; 2)

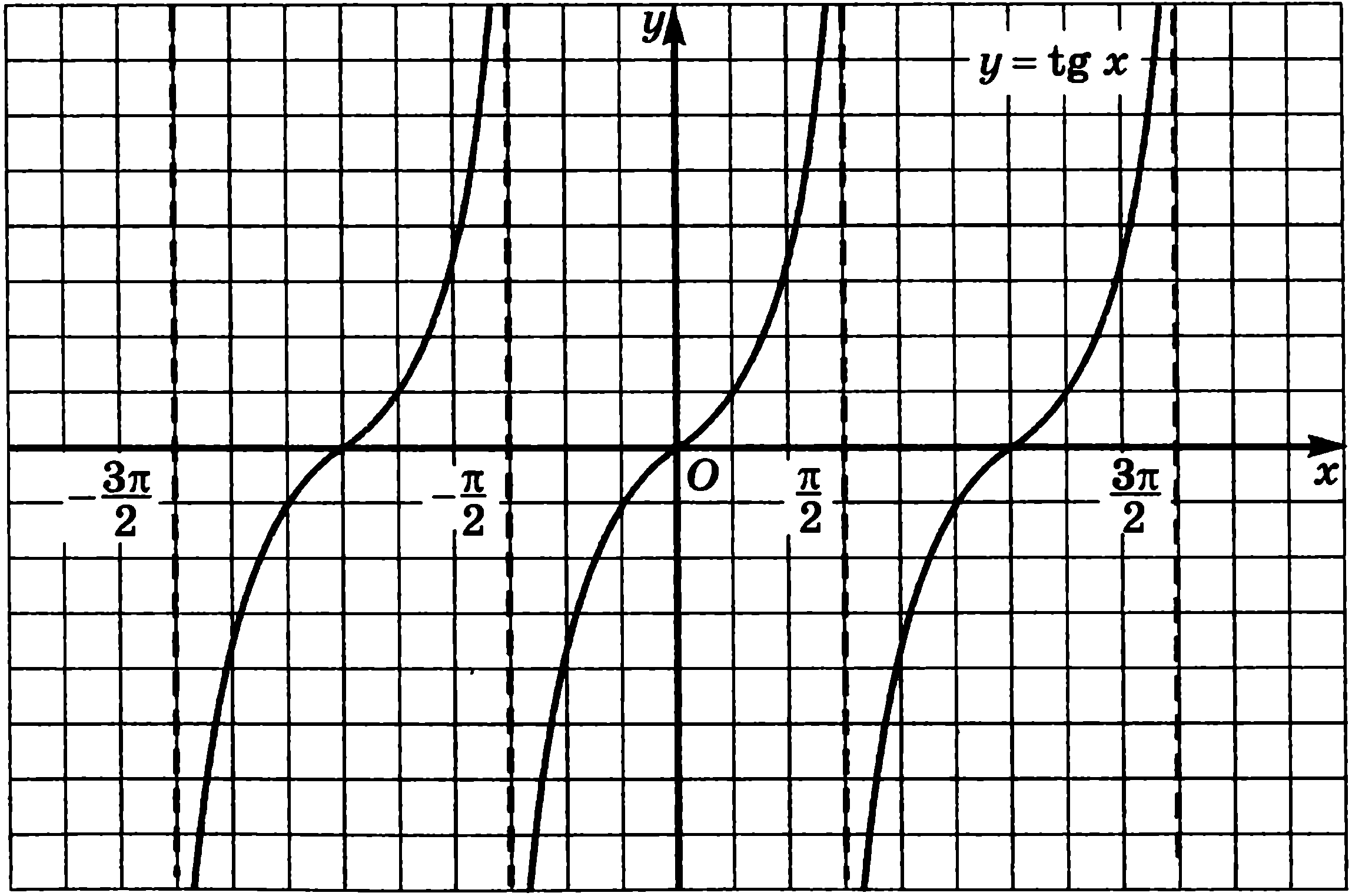
Ответ: 1) _______

2) _______

3) 4)

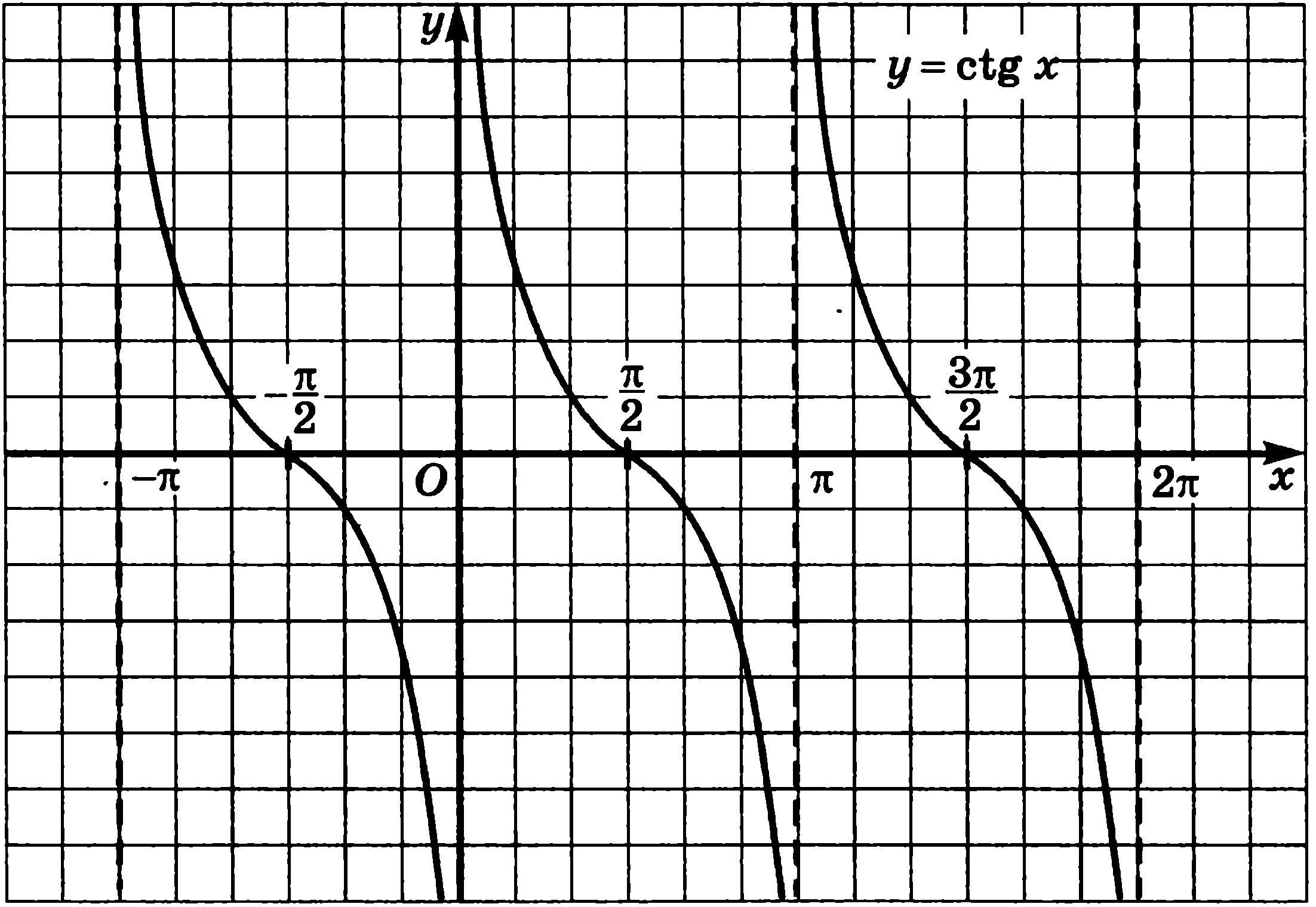
Ответ: 3) _______

4) ______

ПРЕОБРАЗОВАНИЯ ГРАФИКОВ
ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ

Определение:

Преобразования графиков функций — это линейные преобразования функции y = f(x) или её аргумента x к виду y=af(kx+b) +m,а также преобразование с использованием модуля.

Зная, как строить графики функции y = f(x),гдеy=sinx, y=cosx, y = tgx, y = ctgx, можно построить график функции y=af(kx+b)+ m.

Общий вид функции	Преобразования
Параллельный перенос графика вдоль Ох на b единиц
y = f(x − b)	вправо.
y = f(x + b)	влево
Параллельный перенос графика вдоль Оу на m единиц
y = f(x) + m	вверх
y = f(x) - m	вниз
Отражение графика
y = f(− x)	симметрично относительно Оу.
y = − f(x)	Симметрично относительно Ох.
Сжатие и растяжение графика
y = f(kx)	k > 1 — сжатие графика к Оу в k раз, 0 < k < 1 — растяжение графика от Оу в k раз.
y = kf(x)	При k > 1 — растяжение графика от оси абсцисс в k раз, при 0 < k < 1 — сжатие графика к оси абсцисс в k раз.
Преобразования графика с модулем
y = | f(x) |	f(x) > 0 — график остаётся без изменений, f(x) < 0 — график симметрично отражается относительно Ох.
y = f(| x |)	— график остаётся без изменений, x < 0 — график симметрично отражается относительно Оу.

ПРЕОБРАЗОВАНИЕ ГРАФИКА ФУНКЦИИ СИНУС.

Параллельный перенос

Построить график функции

Построить график функции

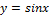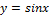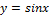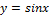Отражение графика.

Построить график функции .

Построить график функции .

Сжатие и растяжение графика.

Построить графики функций и

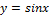Построить графики функци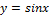й и

Преобразование графика с модулем.

Построить график функции

Построить график функции

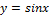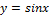Примеры построения

Пример 1. Построить график функции

Решение: Преобразуем функцию

1. Строим график функции

2. Параллельным переносом вдоль оси х переносим функцию на вправо

3. Сжимаем полученный график к Оу в 2 раза:

4. Растягиваем полученный график от оси х в 2 раза. Получаем искомый график функции

Пример 2. Построить график функции

1. Строим график функции

2. Параллельным переносом вдоль оси ____ переносим функцию _______________

3. Сжимаем полученный график к оси ___ в ___ раз(а):

4. Растягиваем полученный график от оси __ в __ раз(а). Получаем искомый график функции

Поэтапно построить график функции