Точечные оценки параметров генеральной совокупности

Во многих случаях мы располагаем информацией о виде закона распределения случайной величины (нормальный, бернуллиевский, равномерный и т. п.), но не знаем параметров этого распределения, таких как Mx, Dx. Для определения этих параметров применяется выборочный метод.

Пусть выборка объема n представлена в виде вариационного ряда. Назовем выборочной средней величину

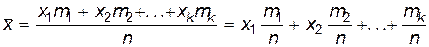(10.1.3)

Величина 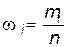называется относительной частотой значения признака x_i. Если значения признака, полученные из выборки не группировать и не представлять в виде вариационного ряда, то для вычисления выборочной средней нужно пользоваться формулой

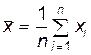. (10.1.4)

Естественно считать величину 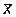выборочной оценкой параметра Mx. Выборочная оценка параметра, представляющая собой число, называетсяточечной оценкой.

Выборочную дисперсию

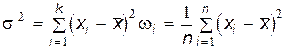(10.1.5)

можно считать точечной оценкой дисперсии Dx генеральной совокупности.

Приведем еще один пример точечной оценки. Пусть каждый объект генеральной совокупности характеризуется двумя количественными признаками x и y. Например деталь может иметь два размера – длину и ширину. Можно в различных районах измерять концентрацию вредных веществ в воздухе и фиксировать количество легочных заболеваний населения в месяц. Можно через равные промежутки времени сопоставлять доходность акций данной корпорации с каким-либо индексом, характеризующим среднюю доходность всего рынка акций. В этом случае генеральная совокупность представляет собой двумерную случайную величину x,h. Эта случайная величина принимает значения x, y на множестве объектов генеральной совокупности. Не зная закона совместного распределения случайных величин x иh, мы не можем говорить о наличии или глубине корреляционной связи между ними, однако некоторые выводы можно сделать, используя выборочный метод.

Выборку объема n в этом случае представим в виде таблицы, где
i-тый отобранный объект (i= 1,2,...n)представлен парой чисел x_i, y_i :

x1	x2	...	xn
y1	y2	...	yn

Выборочный коэффициент корреляции рассчитывается по формуле

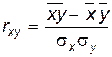(10.1.6)

Здесь

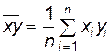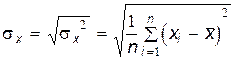, , (10.1.7)

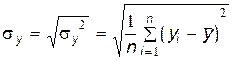. (10.1.8)

Выборочный коэффициент корреляции можно рассматривать как точечную оценку коэффициента корреляции r_xh, характеризующего генеральную совокупность.

Выборочные параметры 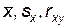или любые другие зависят от того, какие объекты генеральной совокупности попали в выборку и различаются от выборки к выборке. Поэтому они сами являются случайными величинами.

Пусть выборочный параметр dрассматривается как выборочная оценка параметра D генеральной совокупности и при этом выполняется равенство

Md =D. (10.1.9)

Такая выборочная оценка называется несмещенной.

Для доказательства несмещённости некоторых точечных оценок будем рассматривать выборку объема n как систему n независимых случайных величин x₁,x₂,... x_n , каждая из которых имеет тот же закон распределения с теми же параметрами, что и случайная величина x, представляющая генеральную совокупность. При таком подходе становятся очевидными равенства

Mx_i = Mx_i =Mx;
Dx_i = Dx_i =Dx для всех k = 1,2,...n.

Теперь можно показать, что выборочная средняя есть несмещенная оценка средней генеральной совокупности или, что- то же самое, математического ожидания интересующей нас случайной величины x :

.

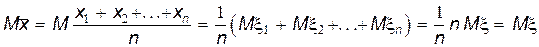Выведем формулу для дисперсии выборочной средней:

.

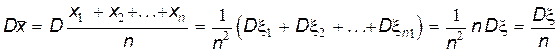Найдем теперь, чему равно математическое ожидание выборочной дисперсии s ². Сначала преобразуем s ² следующим образом:

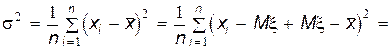
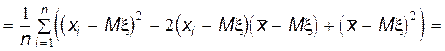
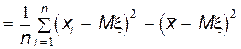
Здесь использовано преобразование:

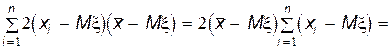
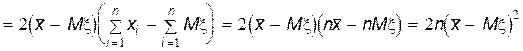
Теперь, используя полученное выше выражение для величины s ², найдем ее математическое ожидание.

.

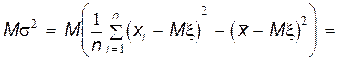
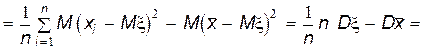
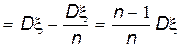Так как Ms ² ¹ Dx, выборочная дисперсия не является несмещенной оценкой дисперсии генеральной совокупности.

Чтобы получить несмещенную оценку дисперсии генеральной совокупности, нужно умножить выборочную дисперсию на 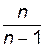. Тогда получится величина 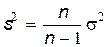, называемая исправленной выборочной дисперсией.

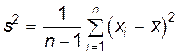(10.1.10)

Пусть имеется ряд несмещенных точечных оценок одного и того же параметра генеральной совокупности. Та оценка, которая имеет наимень­шую дисперсию называется эффективной.

Полученная из выборки объема n точечная оценка d_n параметра D генеральной совокупности называетсясостоятельной, если она сходится по вероятности к D. Это означает, что для любых положительных чисел e и g найдется такое число n_eg , что для всех чисел n, удовлетворяющих неравенству n > n_eg выполняется условие .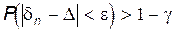

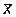и 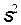являются несмещёнными, состоятельными и эффективными оценками величин Mx и Dx.