Как строится эпюра нормальных напряжений при косом изгибе?
Зная положение НЛ, легко построить эпюру 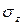 . Для этого, например, справа от сечения (см. рис. 9.2) проведем перпендикуляр к НЛ. По нормали к нему и будем откладывать значения напряжений. Как уже отмечалось выше, они будут изменяться по линейному закону, при этом наибольшие растягивающие напряжения возникают в точке 1, а наибольшие сжимающие – в точке 2.
. Для этого, например, справа от сечения (см. рис. 9.2) проведем перпендикуляр к НЛ. По нормали к нему и будем откладывать значения напряжений. Как уже отмечалось выше, они будут изменяться по линейному закону, при этом наибольшие растягивающие напряжения возникают в точке 1, а наибольшие сжимающие – в точке 2.
Чем опасен косой изгиб?
Выполним некоторые вычисления для рассмотренного нами случая. Пусть, например, 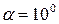 (см. рис. 9.2), то есть перекос является относительно малым.
(см. рис. 9.2), то есть перекос является относительно малым.
При отсутствии перекоса, то есть при прямом изгибе, наибольшие нормальные напряжения в балке, например в точке 1, были бы равны:
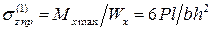 .
.
При косом изгибе в этой же точке они определяются по формуле
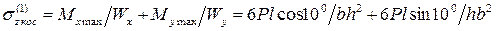 .
.
Определим, во сколько раз наибольшие напряжения при наличии технологического брака больше, чем при его отсутствии. Составим отношение найденных выражений для напряжений:
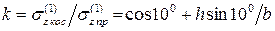 .
.
Например, при отношении 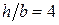 получим
получим
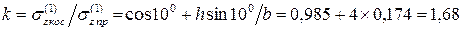 ,
,
то есть напряжения в балке возрастают почти на 70 %.
Таким образом, даже небольшой технологический перекос может привести к существенному увеличению нормальных напряжений в балке.
9.7. В какой точке поперечного сечения балки возникает наибольшее касательное напряжение?
В рассматриваемом нами примере нагрузки 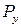 и
и 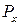 вызывают во всех поперечных сечениях одинаковые перерезывающие силы, абсолютные значения которых соответственно равны:
вызывают во всех поперечных сечениях одинаковые перерезывающие силы, абсолютные значения которых соответственно равны:
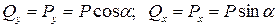 .
.
Наибольшие касательные напряжения от  возникают в точках, лежащих на оси x, а от
возникают в точках, лежащих на оси x, а от 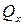 – в точках, лежащих на оси y. Эти напряжения определяются по формулам
– в точках, лежащих на оси y. Эти напряжения определяются по формулам
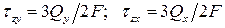 ,
,
где 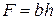 – площадь поперечного сечения балки.
– площадь поперечного сечения балки.
Наибольшее касательное напряжение при косом изгибе возникает в центре тяжести поперечного сечения. Его можно найти как следующую геометрическую сумму:
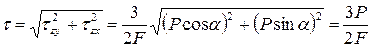 .
.
9.8. Как определяются прогибы при косом изгибе?
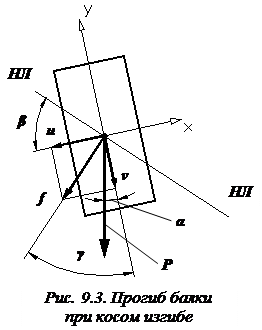
Сначала найдем прогиб консоли от каждой из составляющих силы P в отдельности. Обозначим прогиб балки по направлению осей x и y соответственно через u и v (рис. 9.3). Тогда: 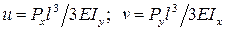 .
.
 Суммарный прогиб консоли равен:
Суммарный прогиб консоли равен:
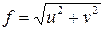 .
.
Найдем направление результирующего перемещения f. Для этого определим значение угла наклона 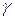 этого перемещения к вертикальной оси y:
этого перемещения к вертикальной оси y:
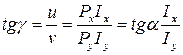 . (9.6)
. (9.6)
Сопоставляя формулы (9.5) и (9.6), видим, что абсолютные значения углов 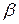 и
и 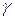 равны между собой.
равны между собой.
Следовательно, направление суммарного прогиба балки при косом изгибе перпендикулярно нулевой линии (см.
рис. 9.3).
Отсюда можно сделать важный вывод о том, что направление суммарного прогиба балки f при косом изгибе (когда 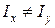 ) не совпадает с направлением действующей силы P, то есть
) не совпадает с направлением действующей силы P, то есть 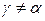 .
.
Внецентренное сжатие
Многие элементы машин и сооружений одновременно испытывают деформации изгиба (прямого или косого) и растяжения (сжатия).
В этом случае в поперечных сечениях стержня могут возникнуть пять внутренних силовых факторов из шести (исключая крутящий момент 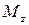 ).
).
В настоящем беседе мы рассмотрим частный случай такого вида деформации, называемый внецентренным сжатием (рис. 10.1), когда в поперечных сечениях стержня возникают только три силовых фактора: продольная сила 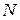 и два изгибающих момента
и два изгибающих момента 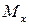 и
и 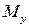 .
.
Будем считать, что стержень обладает большой жесткостью на изгиб. Это допущение мы будем использовать при вычислении изгибающих моментов от продольной силы 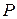 , пренебрегая прогибом стержня.
, пренебрегая прогибом стержня.
Задача о внецентренном сжатии стержня (массивной колонны) впервые была рассмотрена Юнгом в 1802 г.
