Построение линейной производственной модели рельсосварочного поезда

Петербургский государственный университет путей сообщения

Кафедра «Экономика и менеджмент в строительстве»

Курсовая работа по дисциплине «ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ»

Тема работы:

«ПОСТРОЕНИЕ ЭКОНОМИКО–МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ И АНАЛИЗ ПРОИЗВОДСТВЕННОЙ ДЕЯТЕЛЬНОСТИ ПРЕДПРИЯТИЙ ЖЕЛЕЗНОДОРОЖНГО ТРАНСПОРТА»

Выполнила: Студент учебной группы ЭБС - 101	Кузнецова А.И.
Проверил: Руководитель профессор	П. В. Герасименко

Санкт-Петербург

«УТВЕРЖДАЮ»

Заведующий кафедрой «Экономика и менеджмент в строительстве»

профессор С. Г. Опарин

« » сентября 20012 г.

З А Д А Н И Е на КУРСОВУЮ РАБОТУ

по дисциплине «ЭКОНОМИКО–МАТЕМАТИЧЕСКИЕ МОДЕЛИ»

Студент ЭБС - 101 учебной группы Кузнецова А.И.

Выдано……. сентября 2012 г. Срок защиты…...декабря 2012 г.

Руководитель: профессор П. В. Герасименко

Цель работы

Целью курсовой работы является освоение и отработка навыков использования основных экономико-математических моделей и стандартных компьютерных процедур построения и анализа моделей в процессе решения прикладной задачи, связанной с моделированием производственной деятельности рельсосварочного поезда по статистическим данным за годовой период (12 месяцев).

Исходные данные

Для разработки математической модели используются опытные данные, представленные в табл. 1.1.

Таблица 1.1

Вариант № 1

Месяц	Y, пр. км	K, млн. руб.	L, тыс. руб.
	91,3	195,704	3,8592
	115,5	193,518	3,6702
	108,9	191,333	3,8255
	187,4	189,148	3,7571
	207,2	186,963	4,0403
	154,4	185,100	4,0417
	185,2	182,961	4,464
	191,4	180,823	4,17
	183,5	178,684	4,488
		176,546	4,624
	185,5	174,411	3,628
	138,1	334,003	3,828

Этапы и требования к выполнению разделов работы

1. Подготовительный – подбор и ознакомление с литературой, обоснование актуальности исследования, изучение подходов к решению поставленной задачи.

2. Моделирования – обоснование применения методов математического моделирования решения задачи; осмысливаются все понятия и зависимости, на которых базируются модели; обоснование и выбор производственных моделей.

3. Алгоритмизации и программирования – изучение алгоритмов и программ расчетов на ПЭВМ. При выборе программного обеспечения можно остановиться на прикладных пакетах программ или создать собственный программный продукт.

4. Расчетный – применение алгоритма и программы для вычислений параметров производственных моделей.

5. Анализа – оценки тесноты связи между показателями производственной модели и погрешности вычислений; раскрытие сущности полученных результатов, их взаимосвязи с исходными данными. Для проведения анализа рекомендуется использовать различные виды наглядности: схемы, графики, диаграммы, таблицы и т. п.

6. Заключительный – оформление расчетно-пояснительной записки и подготовка к защите.

Представить

Пояснительную записку, которая должна содержать: титульный лист, оглавление и введение; краткие теоретические сведения по моделированию; необходимые аналитические зависимости и расчетные формулы; схемы алгоритмов и программы решения задач; результаты расчетов, оформленные в виде таблиц, диаграмм и графиков; анализ полученных результатов; список литературы.

Список рекомендуемой литературы

1. Герасименко П.В. Специальные разделы высшей математики для экономических специальностей, ч.1: Учебное пособие – СПб.: Петербургский государственный университет, 2005. – 40 с.

2. Герасименко П.В. Специальные разделы высшей математики для экономических специальностей, ч.2: Учебное пособие – СПб.: Петербургский государственный университет, 2006. – 48 с.

3. Герасименко П.В. Специальные разделы высшей математики для экономических специальностей, ч.3: Учебное пособие – СПб.: Петербургский государственный университет, 2005. – 43 с.

4. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. – М.: МГУ, 2001. – 368 с.

5. Кремер Н.Ш., Путко Б.А. Эконометрика. – М.: ЮНИТИ-ДАНА, 2003. – 311 с.

6. Эконометрика: Учебник /Под ред. И. И. Елисеевой. – М.: Финансы и статистика, 2002. – 344 с.

Задание принял к исполнению

« » сентябрь 2012 г. (подпись)

Содержание

Введение
1. Построение линейной производственной модели рельсосварочного поезда
Выводы

Введение.

В условиях реформирования железнодорожного транспорта требуется создание новой, эффективной, ориентированной на рыночную экономику, системы технического обслуживания железнодорожного пути. Поддержания пути в работоспособном состоянии – основная цель системы технического обслуживания железнодорожного пути, основанная на использовании комплекса технических, организационных, технологических средств. Поэтому создание новых и модернизация существующих средств технического обслуживания железнодорожного пути является актуальной задачей.

Техническим средством путевого хозяйства, направленным на формирование управляющих воздействий на путь, является комплекс специального подвижного состава, самоходных и несамоходных путевых машин. Они применяются при текущем содержании и ремонтах железнодорожного пути, а также вагонов и других транспортных средств, используемых при доставке материалов верхнего строения пути к месту производства работ, очистке пути от снега, удаление растительности и т.п.

ОАО «РЖД» принадлежит большое количество СПС (самоходных путевых средств), нормативный срок которых истек и которые по формальным причинам должны быть списаны. Однако, при одномоментном списывании всей номенклатуры СПС и ограниченных средствах на поставку новых, приведет к снижению объема ремонтов железнодорожного пути и в конечном итоге к снижению уровня безопасности на железных дорогах.

Ранее, на уровне практического решения, проблема оценки дохода от ресурсов СПС хозяйства пути по производственной модели не ставилась по ряду объективных и субъективных причин. Поэтому весьма актуально создание методики оценки дохода от ресурсов СПС, которая должна включать построение производственных моделей отдельных подразделений СПС. Построение модели должно базироваться на статистических данных, которые учитывают реальное состояние СПС

Построение линейной производственной модели рельсосварочного поезда

1.1 Алгоритм расчета параметров линейной производственной модели рельсосварочного поезда

Линейная производственная модель рельсосварочного поезда является линейной регрессией. Она имеет вид:

,

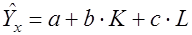где

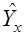– результативный признак, характеризующий объем производства (ОП) рельсосварочного поезда;

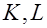– фактор (ресурсы), соответственно основные производственные фонды (ОПФ) и фонды оплаты труда (ФОТ);

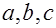– параметры линейной производственной модели.

Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессии используется метод наименьших квадратов. Он позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака 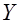от теоретических значений 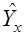будет минимальной. В этом случае для определения параметров a, b и 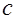линейной регрессии необходимо по опытным значениям 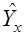и 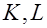вычислить следующие их средние значения и средние значения их произведений и квадратов по следующим соотношениям:

; ; ;

; ; ;

; ; .

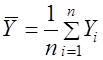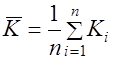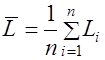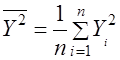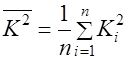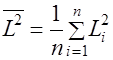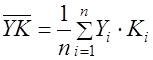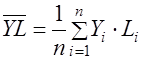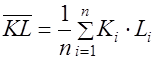После применения метода наименьших квадратов можно получить систему уравнений в векторно-матричной форме:

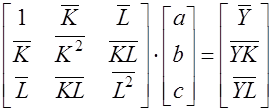
Решение системы, т.е. нахождение параметров модели, можно выполнить методом Крамера. Для его реализации необходимо вычислить четыре следующих определителя:

,

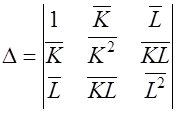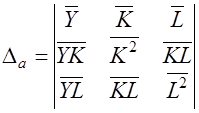
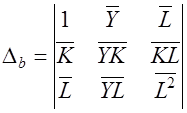
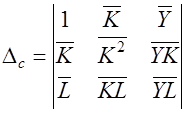
Тогда вычисление параметров модели можно осуществить по следующим формулам:

, , .

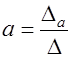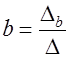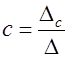1.2. Расчет параметров линейной производственной модели

рельсосварочного поезда

На основании исходных данных выполнены расчеты, которые при 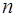= 12 представлены в табл. 2.

Таблица 2.1

№№
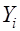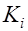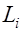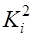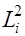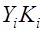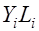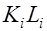	91,3	195,704	3,8592	38300,05562	14,89342464	17867,7752	352,34496	755,2608768
	115,5	193,518	3,6702	37449,21632	13,47036804	22351,329	423,9081	710,2497636
	108,9	191,333	3,8255	36608,31689	14,63445025	20836,1637	416,59695	731,9443915
	187,4	189,148	3,7571	35776,9659	14,11580041	35446,3352	704,08054	710,6479508
	207,2	186,963	4,0403	34955,16337	16,32402409	38738,7336	837,15016	755,3866089
	154,4	185,100	4,0417	34262,01	16,33533889	28579,44	624,03848	748,11867
	185,2	182,961	4,464	33474,72752	19,927296	33884,3772	826,7328	816,737904
	191,4	180,823	4,17	32696,95733	17,3889	34609,5222	798,138	754,03191
	183,5	178,684	4,488	31927,97186	20,142144	32788,514	823,548	801,933792
		176,546	4,624	31168,49012	21,381376	30365,912	795,328	816,348704
	185,5	174,411	3,628	30419,19692	13,162384	32353,2405	672,994	632,763108
	138,1	334,003	3,928	111558,004	15,429184	46125,8143	542,4568	1311,963784
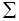	1920,4	2369,194	48,496	488597,0759	197,2046903	373947,1569	7817,31679	9545,387464
Cр. зн.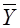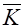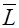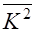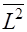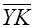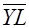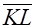
	160,0333	197,4328	4,041333	40716,42299	16,43372419	31162,26308	651,4430658	795,4489553

С учетом средних значений, вычисленных и представленных в Таблице 2, составим определители.

Таблица 2

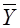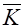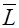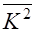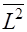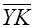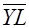160,0333	197,4328	4,041333	40716,42299	16,43372419	31162,26308	651,4430658	795,4489553

∆ =

= 1•40716,42299•16,43372419 - 1•795,4489553•795,4489553 – 197,4328•197,4328•16,43372419 +

+ 197,4328•4,041333•795,4489553 + 4,041333•197,4328•795,4489553 –

– 4,041333•4,041333•40716,42299 = 170,05193620466

∆a=

= 160,0333•40716,42299•16,43372419 – 160,0333•795,4489553•795,4489553 –

– 31162,26308•197,4328•16,43372419 + 31162,26308•4,041333•795,4489553 +

+651,4430658•197,4328•795,4489553 – 651,4430658•4,041333•40716,42299 = 4951,2848640978

∆b=

= 1•31162,26308•16,43372419 - 1•795,4489553•651,4430658 – 197,4328•160,0333•16,43372419 +

+ 197,4328•4,041333•651,4430658 + 4,041333•160,0333•795,4489553 –

– 4,041333•4,041333•31162,26308 = -32,472866618482

∆c=

= 1•40716,42299•651,4430658 - 1•31162,26308•795,4489553 – 197,4328•197,4328•651,4430658 +

+ 197,4328•160,0333•795,4489553 + 4,041333•197,4328•31162,26308 –

- 4,041333•160,0333•40716,42299 = 7095,1581170484

Тогда параметры линейной производственной модели примут следующие величины:

;

;

.

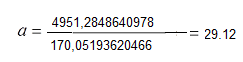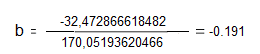Таким образом, линейная производственная модель рельсосварочного поезда имеет вид: