И способах их определения

n – нормаль в точке Q

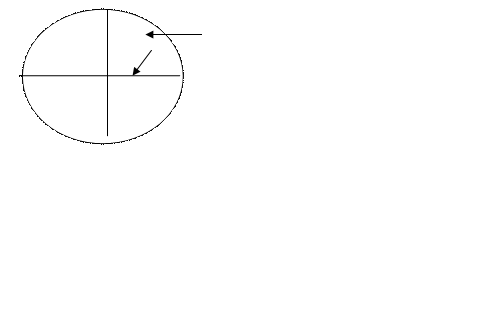_{Q u– уклонение отвеса}

g– направление силы тяжести в точке Q

в– геодезическая широта точки Q

Угол uмежду вектором g силы тяжести и вектором n нормали в точке Q поверхности эллипсоида называют уклонением отвесной линии.Для общеземногоэллипсоида такой угол принято называть абсолютным, а для референц-эллипсоида- относительным уклонением отвеса.

Уклонение отвесной линии представляют обычно в виде составляющих в плоскости меридиана через ξ(кси) и в плоскости первого вертикала – через η (эта). При этом имеет место: u² = ξ² + η².

Можно вычислить значения ξи ηдля точки Q,если знать астрономические и геодезические координаты этой точки (φ,λ и В,L).

Для перехода от астрономических к геодезическим координатам используют выражения:

B = φ - ξ; L = λ - η sec φ; A = α – η tg φ + (η cos α - ξ sin α) ctg z₀,

где α –астрономический азимут.

Понятие уклонение отвеса является одним из важнейших понятий геодезии и теории фигуры Земли. В равнинных областях составляют единицы и доли секунд, а в горах – несколько десятков угловых секунд.

Редуцирование горизонтальных углов

Каждый измеренный горизонтальный угол образован двумя горизонтальными направлениями (сторонами). Поэтому возникает необходимость редуцирования измеренного угла по двум его направлениям 1 - 2 в отдельности путем введения в них поправок:

1) V”₁ = (η”₁ cos A₁₂ - ξ”₁ sin A₁₂) ctg Z₁₂ - поправка за уклонение отвесной линии на пункте наблюдения 1;

H₂

2)V”₂ = ρ”e² ---------cos²B₂ sin2 A₁₂ - поправка за высоту

2Mнаблюдаемого пункта 2

где М и H₂ - в км.

S²

3) V”₃ = ρ” (e¹)² -------- cos²B₁ sin2 A₁₂ - поправка за переход от

12N²₁ нормального сечения к

геодезической линии

Например, для эллипсоида Красовского:

v₃” = 0,0282 S² cos² B₁ sin 2A₁₂,где S² - в сотнях км.

Для сторон до 50 км эта поправка не учитывается .

Полное значение поправки δ_ik в каждое направление определяется суммой поправок:

δ_ik = Σ V_ik .

Поправка в угол вычисляется как разность поправок смежных направлений («право минус лево»):δ _А = δ_АВ – δ_АС.

Сумма поправок в три угла треугольника теоретически равна сферическому избытку со знаком минус: ε = - (δ_А+δ_В+δ_С), так как

Редуцированные углы получаем сферическими.

Редуцирование сторон

S 2 Измеренная сторона S редуцируется

1 в два этапа: сначала определяется хорда

H₂ d, а затем уже значение длины S₀ на

H₁ S₀ эллипсоиде. d

R R 1) вычисление хорды d:

α

(S +∆H)( S - ∆H)

d = --------------------------- .

(1 + H₁/ R)(1 + H₂/R)

2)вычислениеS₀н а эллипсоиде :

d³

S₀ = d + ----------- .

24R²

3)вычисление поправки в наклонное расстояние:

∆S м = S₀ – S.

Очевидно, что поправка ∆S имеет всегда отрицательное значение.

Лекция 10. О редукции точек с поверхности эллипсоида на