Методы полиномиальной аппроксимации

Пусть точным решением задачи (1) является полином степени :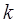

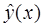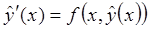Предположим, что нам известны значения точного решения и правой части дифференциального уравнения в 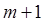точках 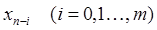. Нашей целью является построение таких численных методов, которые позволили бы в этом случае найти 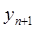, совпадающее со значением точного решения в точке 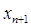: 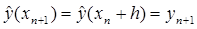. Например, для 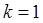в (21) это позволяет сделать явный метод Эйлера.

Любой метод, дающий возможность найти точное значение 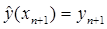решения 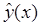задачи (1), являющегося полиномом (21), называют методом полиномиальной аппроксимации (формулой численного интегрирования) порядка .

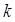Предупреждение.Не путать порядок 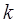метода полиномиальной аппроксимации с порядком 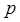метода Тейлора.

В отличие от метода Тейлора большинство методов полиномиальной аппроксимации использует для вычисления 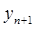информацию о нескольких предыдущих шагах. Поэтому метод полиномиальной аппроксимации при 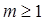называютмногошаговымв отличие, например, от методов Рунге-Кутта, которые являются одношаговыми.

Общий вид алгоритма метода полиномиальной аппроксимации:

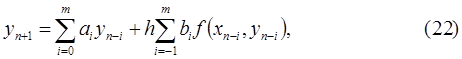
где 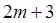коэффициентов 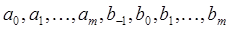определяются так, что если точное решение 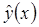задачи (1) является полиномом степени 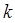и если предварительно найденные значения 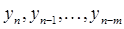являются точным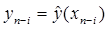и ( при 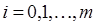), то алгоритм (22) дает точное значение решения 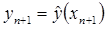. Очевидно, что 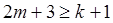(число параметров - коэффициентов метода должно быть больше числа коэффициентов полинома (21)).

Найдем условия, которым должны удовлетворять коэффициенты 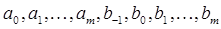метода полиномиальной аппроксимации порядка .

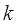Семейство задач Коши, решением которых является полином (21), имеет вид

Для удобства вычислений положим 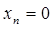. Тогда 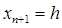, 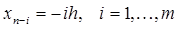. Из (21) и (23) имеем:

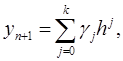
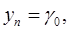
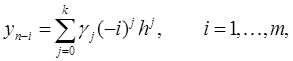
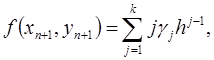
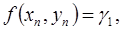
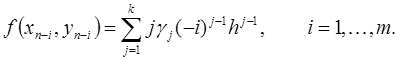
Подставляя найденные выражения в (22) и приравнивая коэффициенты при 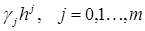, получим систему 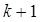уравнений относительно 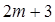неизвестных :

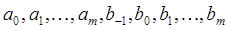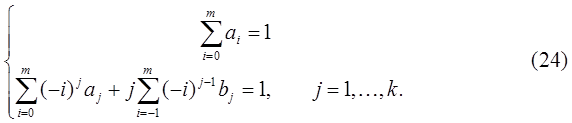
Система (24) называется условием корректности многошагового метода полиномиальной аппроксимации порядка .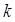

Замечание. Если потребовать, чтобы метод был точен для случая, когда решение задачи (1) принадлежит специальному классу функций иных, чем полиномы (например, экспоненциальных), то можно получить другие условия корректности приближенного метода.

Метод полиномиальной аппроксимации (22), коэффициенты которого 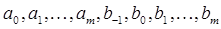удовлетворяют условию корректности (24), называют состоятельным.

Метод (22) называется явным, если 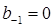, и неявным, если .

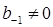Локальная алгоритмическая ошибка состоятельного многошагового метода полиномиальной аппроксимации порядка 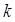при естественных ограничениях на правую часть дифференциального уравнения 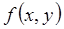определяется выражением

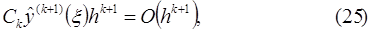
где 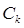- константа, не зависящая от , .

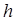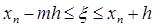Опишем два важных семейства состоятельных методов полиномиальной аппроксимации, часто используемые в вычислительной практике.

Метод Адамса-Башфорта (экстраполяционный метод Адамса).

Метод Адамса-Башфорта порядка 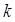является явным многошаговым методом полиномиальной аппроксимации, полученным из (22) при условии

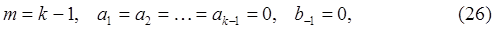
то есть

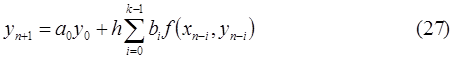
Коэффициенты метода 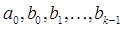определяются из условия корректности (24). В этом случае (24) примет вид

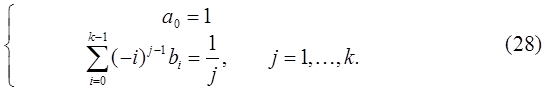
Определитель этой системы отличен от нуля и, следовательно, существует единственное решение. Таким образом, для любого 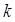решение системы (28) однозначно определяет метод Адамса-Башфорта порядка 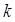(метод является состоятельным).

Таблица 1. Алгоритмы метода Адамса-Башфорта.

Порядок	Алгоритм
Первый	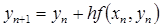(явный метод Эйлера)
Второй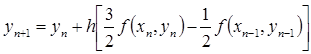
Третий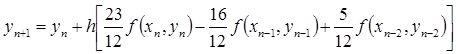
Четвертый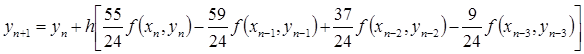

Для численной реализации метода Адамса-Башфорта порядка 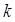требуется 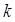стартовых значений 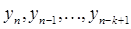(метод является 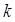- шаговым).

Метод Адамса-Мултона (интерполяционный метод Адамса).

Метод Адамса-Мултона порядка 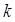является неявным многошаговым методом полиномиальной аппроксимации, полученным из (22) при условии

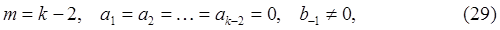
то есть

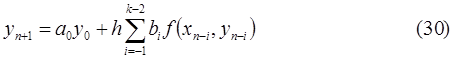
Коэффициенты метода 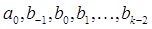определяются из условия корректности (24). В этом случае (24) примет вид

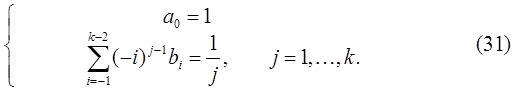
Определитель этой системы отличен от нуля и, следовательно, существует единственное решение. Таким образом, для любого 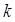решение системы (31) однозначно определяет метод Адамса-Мултона порядка 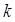(метод является состоятельным).

Для численной реализации метода Адамса-Мултона порядка 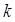требуется 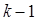стартовых значений 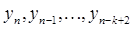(метод является 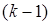- шаговым).

Таблица 2. Алгоритмы метода Адамса-Мултона.