Приложение. Основные сведения по динамике вращательного движения твердого тела вокруг неподвижной оси

Движение твердого тела, при котором две его точки остаются неподвижными, называется вращением тела вокруг неподвижной оси. Прямая, соединяющая эти точки, называется осью вращения тела. При вращении вокруг неподвижной оси все точки тела описывают окружности, центры которых лежат на оси вращения, а плоскости перпендикулярны к ней. Положение твердого тела в пространстве полностью определяется значением φ угла поворота тела из некоторого начального положения.

Для характеристики быстроты вращения тела вокруг оси служит угловая скорость. Угловой скоростью называется быстрота изменения (точнее, производная) угла поворота φ по времени:

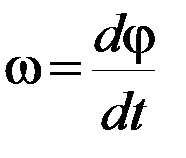(П-1)

Вращение считается равномерным, если ω = const.

Величиной, характеризующей быстроту (и направление) изменения угловой скорости, является угловое ускорение. Производная от угловой скорости или вторая производная угла поворота по времени

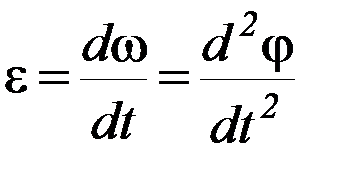(П-2)

Модуль угловой скорости и углового ускорения связаны соответственно с модулями линейной скорости V и линейного ускорения a соотношениями:

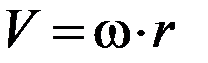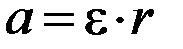, , (П-3)

где r – радиус окружности вращения.

Моментом силы 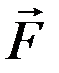относительно неподвижной точки (полюса) называется векторная величина 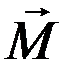, равная векторному произведению радиус-вектора 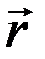, проведенного из этой точки в точку приложения силы, на вектор силы :

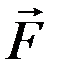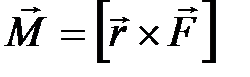(П-4)

Модуль момента силы:

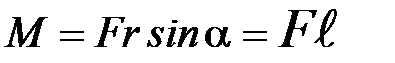, (П-5)

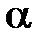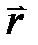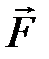где – угол между векторами и , а 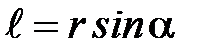– плечо силы.

При переносе точки приложения силы 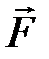вдоль линии её действия момент этой силы относительно одной и той же неподвижной точки не изменяется. Если линия действия силы проходит через точку вращения, то момент силы относительно этой точки равен нулю.

Моментом силы 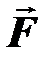относительно неподвижной оси OZ называется скалярная величина М_z, равная проекции на эту ось вектора 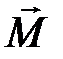момента силы 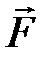относительно произвольной точки на оси. Значение М_z, не зависит от выбора положения точки на оси.

Главный момент относительно неподвижной оси системы сил равен алгебраической сумме моментов относительно этой оси всех сил.

Моментом инерции математической системы относительно неподвижной оси OZ называется физическая величина I_z, равная сумме произведений масс всех N материальных точек на квадраты расстояний до оси OZ:

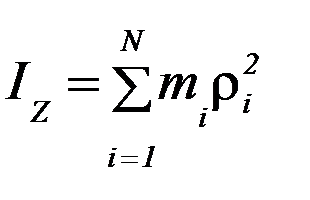, (П-6)

где m_i и ρ_i– массаi-ой точки и ее расстояние от оси.

Момент инерции тела

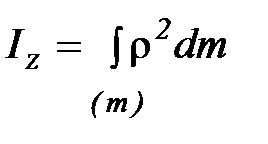(П-7)

где dm = D·dV – масса малого элемента объема тела; dV – объём малого элемента; D – плотность;ρ – расстояние от элемента dm до оси OZ.

Для однородного тела (D = const)

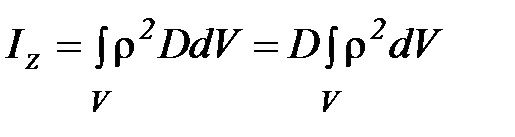(П-8)

Момент инерции тела является мерой инертности во вращательном движении.

Теорема Гюйгенса-Штейнера: Момент инерции тела I относительно произвольной оси равен сумме момента инерции тела I_с относительно оси, проходящей через центр масс тела параллельно данной оси, и произведения массы тела m на квадрат расстояния d между осями:

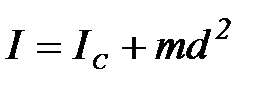(П-9)

8. Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси имеет вид:

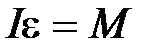, (П-10)

где I– момент инерции тела (системы тел) относительно оси вращения;

М – сумма проекций на ось вращения моментов всех внешних сил, действующих на тело (систему); ε– угловое ускорение.

Контрольные вопросы.

1. Сформулируйте основное уравнение динамики твердого тела для вращательного движения относительно неподвижной оси.

2. Дайте определение момента инерции материальной точки, системы материальных точек и однородного тела относительно неподвижной оси.

3. Приведите аналогии между кинематическими характеристиками вращательного и поступательного движений абсолютно твердого тела; то же динамических характеристик.

4. Какие могут быть причины возникновения ошибок в ходе эксперимента?

5. Сформулируйте теорему Гюйгенса – Штейнера. Каким образом теорема используется в данной лабораторной работе?

6. Дайте определение момента силы относительно неподвижной оси.

7. Запишите основное уравнение динамики для груза, двигающегося поступательно.