Контроль полученных результатов
Для контроля полученных результатов воспользуемся уравнениями кинетостатики в следующем виде:
- в любой момент времени для каждой точки несвободной механической системы геометрическая сумма главных векторов заданных сил, реакций опор и сил инерции материальных точек системы равна нулю
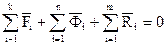 (3.2)
(3.2)
- в любой момент времени для любой точки несвободной механической системы геометрическая сумма главных моментов заданных сил, реакций опор и сил инерции материальных точек системы относительно любого неподвижного центра равна нулю.
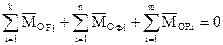 , (3.3)
, (3.3)
где 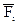 - внешние силы, приложенные к звеньям механизма;
- внешние силы, приложенные к звеньям механизма; 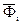 - инерционные силы;
- инерционные силы; 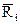 - реакции опор;
- реакции опор; 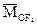 - моменты внешних сил,
- моменты внешних сил, 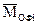 - моменты сил инерции,
- моменты сил инерции, 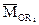 - моменты реакций опор, записанные относительно начала неподвижной системы координат
- моменты реакций опор, записанные относительно начала неподвижной системы координат 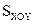 . В этой системе в среде Mathcad рассчитывались функции положения всех точек механизма.
. В этой системе в среде Mathcad рассчитывались функции положения всех точек механизма.
Расчет по формулам (3.2) и (3.3) выполним в векторной форме.
Для этого силы и функции положения (радиус-векторы) точек приложения сил представляются в векторной форме.
Например:
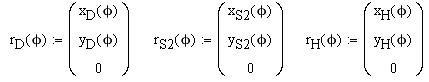
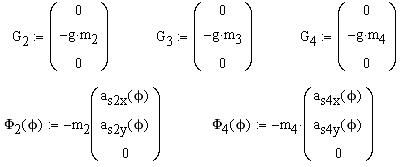
Далее, используя на панели инструментов «Вектор и матрица» кнопку 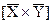 , построим подпрограмму-функцию расчета проекции векторного произведения на орт
, построим подпрограмму-функцию расчета проекции векторного произведения на орт 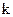

Приведем для некоторого механизма фрагмент записи в системе Mathcad формул (3.2), (3.3). В этих формулах кроме внешних сил и сил инерции учтены реакции во внешних (связанных со стойкой) кинематических парах механизма ( 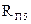 ,
, 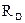 ,
, 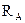 ):
):
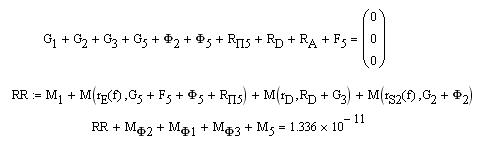
Полученный результат (нулевой вектор в первом уравнении и практический 0 во втором уравнении) свидетельствует о том, что силовой расчет механизма был выполнен верно.
3.2. Применение принципа возможных перемещений в силовом расчете механизмов.
Принцип возможных перемещений – один из вариационных принципов аналитической механики, устанавливающий общее условие равновесия механической системы.
Согласно этому принципу для равновесия механической системы с идеальными связями (идеальными называют связи, сумма элементарных работ сил реакций которых на любом возможном перемещении точек приложения сил равна нулю) необходимо и достаточно, чтобы сумма работ 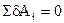 всех приложенных к системе активных сил на любом возможном перемещении системы была равна нулю.
всех приложенных к системе активных сил на любом возможном перемещении системы была равна нулю.
Количество линейно независимых уравнений равновесия, которые можно составить для механической системы исходя из принципа возможных перемещений, равно количеству степеней свободы этой механической системы.
В механизме, степень подвижности которого 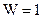 и обобщенная координата есть угол поворота начального звена
и обобщенная координата есть угол поворота начального звена 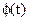 , одно уравнение равновесия, составленное исходя из принципа возможных перемещений, будем использовать для отыскания уравновешивающего момента
, одно уравнение равновесия, составленное исходя из принципа возможных перемещений, будем использовать для отыскания уравновешивающего момента 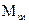 .
.
Применительно к механизмам этот принцип удобно представить в несколько иной форме.
1. Связи в механизме стационарные (Допущение 3). При стационарных связях  действительные перемещения точки
действительные перемещения точки 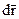 и угловые перемещения звеньев
и угловые перемещения звеньев 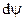 совпадают с одним из возможных перемещений и считаются происходящими во времени. А раз так, то значок вариации
совпадают с одним из возможных перемещений и считаются происходящими во времени. А раз так, то значок вариации 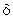 в формуле
в формуле 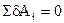 можно заменить на знак дифференциала
можно заменить на знак дифференциала 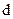 .
.
2. В плоском рычажном механизме все кинематические пары низшие. Поступательная КП позволяет точке, на которую наложена связь, перемещаться только в направлении, перпендикулярном к направлению силы реакции связи. Работа силы реакции такой связи равна нулю и, следовательно, эта связь является идеальной. Вращательные КП являются связями тел вращения. Точки приложения сил реакций этих связей при движении тел не перемещаются. Следовательно, возможная работа этих сил при отсутствии сил трения в шарнирах (Допущение 5) равна нулю. Эти связи также являются идеальными.
3. Механизм не находится в равновесии, поэтому наряду с активными действующими на звенья силами будем учитывать (в соответствии с принципом Даламбера) и силы инерции.
Для механизма принцип возможных перемещений 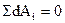 имеет вид:
имеет вид:
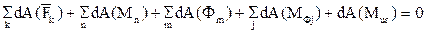 (3.4)
(3.4)
Раскроем в полученном выражении дифференциалы работ:
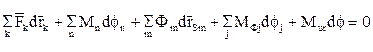 (3.5)
(3.5)
и выразим  из уравнения (3.5) уравновешивающий момент
из уравнения (3.5) уравновешивающий момент 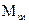 , который подлежит определению:
, который подлежит определению:
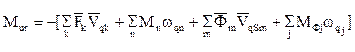 , (3.6)
, (3.6)
где 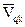 - аналог линейной скорости точки
- аналог линейной скорости точки 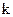 , в которой приложена внешняя сила
, в которой приложена внешняя сила 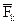 ;
; 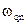 - аналог угловой скорости звена
- аналог угловой скорости звена 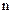 , на котором действует внешний момент
, на котором действует внешний момент 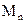 ;
; 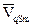 - аналог линейной скорости центра масс звена
- аналог линейной скорости центра масс звена 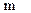 (точка
(точка 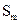 - точка приложения главного вектора сил инерции
- точка приложения главного вектора сил инерции 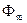 );
);
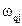 - аналог угловой скорости звена
- аналог угловой скорости звена 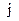 , для которого известен главный приведенный момент инерции
, для которого известен главный приведенный момент инерции 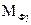 .
.
В формуле (3.6) выражение в 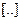 есть приведенный момент всех действующих в механизме сил (включая силы инерции).
есть приведенный момент всех действующих в механизме сил (включая силы инерции).
Уравновешивающий момент 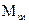 равен суммарному приведенному моменту всех действующих в механизме внешних сил (включая силы инерции, по принципу Даламбера условно отнесенных к внешним), взятому с обратным знаком.
равен суммарному приведенному моменту всех действующих в механизме внешних сил (включая силы инерции, по принципу Даламбера условно отнесенных к внешним), взятому с обратным знаком.
Уравновешивающий момент, рассчитанный по формуле (3.6), сравнивается с моментом 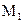 , полученным в результате кинетостатического силового расчета по методике п.3.1.
, полученным в результате кинетостатического силового расчета по методике п.3.1.
Для графоаналитического решения выразим дифференциалы работ в формуле 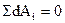 через мощность
через мощность
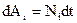
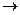
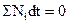
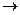
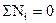 . (3.7)
. (3.7)
Графоаналитический способ решения уравнения 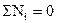 (сумма мгновенных мощностей, развиваемых силами и моментами, действующими на звенья механизма, равна нулю) с целью определения уравновешивающей силы или момента носит название рычага Жуковского.
(сумма мгновенных мощностей, развиваемых силами и моментами, действующими на звенья механизма, равна нулю) с целью определения уравновешивающей силы или момента носит название рычага Жуковского.
Заключение
Материал настоящего учебного пособия дает возможность студенту изучить и практически сразу, выполняя два домашних задания, применить на практике излагаемые в курсе «Теория механизмов и машин» методы структурного, кинематического и кинетостатического анализа плоских рычажных механизмов. В Пособии подчеркивается модульный принцип синтеза и анализа механизма как сложной многозвенной системы, позволяющий каждому студенту для заданного в ДЗ механизма получить алгоритмическую формулу решения поставленных задач, на основании которой с использованием Mathcad-модулей (разработанных в Пособии для каждой кинематически и статически определимой группы) составить алгоритмы и Mathcad-программы расчета исследуемого механизма.
В Пособии приведены примеры реализации полученных алгоритмов в системе Mathcad. Примеры решения перечисленных задач графоаналитическими методами с использованием системы AutoCAD так же приведены в Пособии.
Приложение 1
