Постановка задач линейного программирования и исследование их структуры

Введение

Математическое программирование – это математическая дисциплина, в которой разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями.

Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах математического программирования оказываются непригодными.

Для решения задач математического программирования разработаны и разрабатываются специальные методы и теории. Так как при решении этих задач приходится выполнять значительный объем вычислений, то при сравнительной оценке методов большое значение придается эффективности и удобству их реализации на ЭВМ.

Математическое программирование можно рассматривать как совокупность самостоятельных разделов, занимающихся изучением и разработкой методов решения определенных классов задач.

В зависимости от свойств целевой функции и функции ограничений все задачи математического программирования делятся на два основных класса:

· задачи линейного программирования,

· задачи нелинейного программирования.

Если целевая функция и функции ограничений – линейные функции, то соответствующая задача поиска экстремума является задачей линейного программирования. Если хотя бы одна из указанных функций нелинейна, то соответствующая задача поиска экстремума является задачей нелинейного программирования.

Глава 1. Понятие линейного программирования. Виды задач линейного программирования

Линейное программирование (ЛП) – один из первых и наиболее подробно изученных разделов математического программирования. Именно линейное программирование явилось тем разделом, с которого и начала развиваться сама дисциплина " математическое программирование ". Термин "программирование" в названии дисциплины ничего общего с термином "программирование (т.е. составление программы) для ЭВМ" не имеет, т.к. дисциплина " линейное программирование " возникла еще до того времени, когда ЭВМ стали широко применяться для решения математических, инженерных, экономических и др. задач.

Термин " линейное программирование " возник в результате неточного перевода английского "linear programming". Одно из значений слова "programming" - составление планов, планирование. Следовательно, правильным переводом английского "linear programming" было бы не " линейное программирование ", а "линейное планирование", что более точно отражает содержание дисциплины. Однако, термины линейное программирование, нелинейное программирование, математическое программирование и т.д. в нашей литературе стали общепринятыми и поэтому будут сохранены.

Итак, линейное программирование возникло после второй мировой войны и стало быстро развиваться, привлекая внимание математиков, экономистов и инженеров благодаря возможности широкого практического применения, а также математической стройности.

Можно сказать, что линейное программирование применимо для решения математических моделей тех процессов и систем, в основу которых может быть положена гипотеза линейного представления реального мира.

Линейное программирование применяется при решении экономических задач, в таких задачах как управление и планирование производства; в задачах определения оптимального размещения оборудования на морских судах, в цехах; в задачах определенияоптимального плана перевозок груза (транспортная задача); в задачах оптимального распределения кадров и т.д.

Задача линейного программирования (ЛП), как уже ясно из сказанного выше, состоит в нахождении минимума (или максимума) линейной функции при линейных ограничениях.

Постановка задач линейного программирования и исследование их структуры

Большинство задач, решаемых методами исследования операций, может быть сформулировано так:максимизировать F(x₁, x₂, ., x_n) при ограничениях:

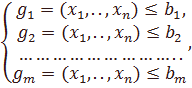(1.1.1)

где f(x₁, x₂, ., x_n) - целевая функция, или критерий эффективности (например, прибыль от производства каких-либо видов продукции, стоимость перевозок и т.п.);

X={x₁,.,x_n} - варьируемые параметры; g₁(x),.,g_m(x) - функции, которые задают ограничения на имеющиеся ресурсы.

В рассматриваемом случае все ограничения имеют вид неравенств. Иногда они могут быть смешанными, то есть неравенства и равенства. Если все ограничения задачи ЛП имеют вид строгих равенств то данная форма записи называется канонической.

Несмотря на требование линейности функций критериев и ограничений, в рамки линейного программирования попадают многочисленные задачи распределения ресурсов, управления запасами, сетевого и календарного планирования, транспортные задачи и прочие.