o Если каждой паре возможных значений случайных величин X и Y соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов X и Y:
 .
.
Далее на примерах будет показано, как найти распределение функции  по известным распределениям слагаемых. Такая задача часто встречается на практике. Например, если Х—погрешность показаний измерительного прибора (распределена равномерно), то возникает задача—найти закон распределения суммы погрешностей
по известным распределениям слагаемых. Такая задача часто встречается на практике. Например, если Х—погрешность показаний измерительного прибора (распределена равномерно), то возникает задача—найти закон распределения суммы погрешностей  .
.
Случай 1.Пусть Х и Y—дискретные независимые случайные величины. Для того чтобы составить закон распределения функции Z=X+Y, надо найти все возможные значения Z и их вероятности. Иными словами, составляется ряд распределения случайной величины Z.
Пример 1. Дискретные независимые случайные величины Х и Y, заданы распределениями
и
Составить распределение случайной величины Z=X+Y.
Возможные значения Z есть суммы каждого возможного
Свойство 3.  , ,  . .  , ,  . Свойство 4.Функция F(x) непрерывна слева. (т.е. . Свойство 4.Функция F(x) непрерывна слева. (т.е.  ). Свойство 5.Вероятность того, что значение случайной величины Х больше некоторого числа х, вычисляется по формуле. ). Свойство 5.Вероятность того, что значение случайной величины Х больше некоторого числа х, вычисляется по формуле.  . Достоверное событие {-∞<x<+∞} представим в виде двух несовместимых событий. . Достоверное событие {-∞<x<+∞} представим в виде двух несовместимых событий.  . Найдем их вероятности . Найдем их вероятности  . Поскольку вероятность достоверного события равна единице, то . Поскольку вероятность достоверного события равна единице, то  . Отсюда . Отсюда  . § 12. Дискретные случайные величины. o Случайная величина Х называется дискретной, если она принимает конечное либо счетное число значений, т.е. Ωх—конечно или счетно. o Законом распределения дискретной случайной величины Х называется совокупность пар чисел вида (хi, рi), где xi—возможные значения случайной величины, а pi—вероятности, с которыми случайная величина принимает эти значения, т.е. . § 12. Дискретные случайные величины. o Случайная величина Х называется дискретной, если она принимает конечное либо счетное число значений, т.е. Ωх—конечно или счетно. o Законом распределения дискретной случайной величины Х называется совокупность пар чисел вида (хi, рi), где xi—возможные значения случайной величины, а pi—вероятности, с которыми случайная величина принимает эти значения, т.е.  , причем , причем  . Простейшей формой задания дискретной случайной . Простейшей формой задания дискретной случайной | |
| 1.рядом распределения | Х | x1 | x2 | … | xn | | | Р | p1 | p2 | … | pn | | | Y | φ(x) | φ(x) | … | φ(x) | | P | p1 | p2 | … | pn | | | | | | | | | | |  . .
Пример 3. Дискретная случайная величина Х задана распределением Найти математическое ожидание функции  . . Возможные значения Y:  ; ;  ; ;  . .
 . .
2. Пусть аргумент Х—непрерывная случайная величина, заданная плотностью распределения р(х). Для нахождения математического ожидания функции  можно сначала найти плотность распределения g(y) величины Y, а затем воспользоваться формулой: можно сначала найти плотность распределения g(y) величины Y, а затем воспользоваться формулой:  . . Если возможны значения  , то , то  . . Пример 4. Случайная величина Х задана плотностью  в интервале (0, π/2); вне этого интервала р(х)=0. Найти математическое ожидание функции в интервале (0, π/2); вне этого интервала р(х)=0. Найти математическое ожидание функции  . . | |
| величины является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности. | X | x1 | x2 | … | xn | … | | P | p1 | p2 | … | pn | … | Такая таблица называется рядом распределения дискретной случайной величины.  Ряд распределения можно изобразить графически. В этом случае по оси абсцисс откладывают значения xi, а по оси ординат—вероятности pi. Полученные точки соединяют отрезками и получают ломаную, которая является одной из форм задания закона распределения дискретной величины. Ряд распределения можно изобразить графически. В этом случае по оси абсцисс откладывают значения xi, а по оси ординат—вероятности pi. Полученные точки соединяют отрезками и получают ломаную, которая является одной из форм задания закона распределения дискретной величины.
Пример. Рассмотрим следующую дискретную случайную величину o Говорят, что дискретная случайная величина Х имеет биномиальное распределение с параметрами (n,p), если она может принимать целые неотрицательные значения  с вероятностями с вероятностями  . . | |
| А) Если различным возможным значениям аргумента функции Y, то вероятность соответствующих значений X и Y между собой равны. Пример 1. Дискретная случайная величина Х задана распределением Найти распределение функции  . . Решение. Найдем возможные значения Х:  , ,  . Искомое распределение Y: . Искомое распределение Y:
Б) Если различным возможным значениям Х соответствуют значения Y, среди которых есть равные между собой, то следует складывать вероятности повторяющихся значений Y. Пример 2. Дискретная случайная величина Х задана распределением Найти распределение функции  . .  , ,  . .
Вероятность возможного значения y1=4 равна сумме вероятностей несовместимых событий Х1=-2, Х2=2, т.е. 0,4+0,5=0,9. Вероятность возможного значения y2=9 равна 0,1. Напишем искомое распределение Х. Пусть задана функция  случайного аргумента Х. Требуется найти математическое ожидание этой функции, зная закон распределения аргумента. случайного аргумента Х. Требуется найти математическое ожидание этой функции, зная закон распределения аргумента. Пусть аргумент Х—дискретная случайная величина с | |
| Пример. µ—число успехов в n испытаниях. µ имеет биномиальное распределение с параметрами (n,p). Обозначают X~B (n,p), т.е. случайная величина Х имеет биномиальное распределение с параметрами (n,p). 
o Говорят, что случайная величина Х имеет распределение Пуассона с параметром λ (λ>0), если она принимает целые неотрицательные значения 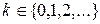 с вероятностями с вероятностями  . . Обозначают  , т.е. случайная величина Х имеет распределение Пуассона с параметром λ. , т.е. случайная величина Х имеет распределение Пуассона с параметром λ.  Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна р (0<p<1) и, следовательно, вероятность его не появления q=1-p. Испытания заканчиваются как только появится событие А. Таким образом, если событие А появилось в k-ом испытании, то в предшествующих k-1 испытаниях оно не появлялось. Обозначим через X дискретную случайную величину—число испытаний, которое нужно провести до первого появления события А. Очевидно, возможными значениями случайной величины Х являются натуральные числа. Пусть в первых k-1 испытаниях событие А не | |
тогда случайная величина Y—непрерывная и имеет плотность  . а) Пусть функция . а) Пусть функция  возрастает. По определению возрастает. По определению  . .  Продифференцируем обе части. Справа получим: Продифференцируем обе части. Справа получим:  , слева— , слева—  , что и требовалось , что и требовалось  . б) Пусть . б) Пусть  убывает. убывает.    . Продифференцировав обе части, . Продифференцировав обе части,  . Покажем, как найти распределение функции случайного аргумента. Пусть аргумент Х—дискретная случайная величина . Покажем, как найти распределение функции случайного аргумента. Пусть аргумент Х—дискретная случайная величина | |
| наступало, а в k-ом испытании появилось. Вероятность этого события  . . o Говорят, что случайная величина Х имеет геометрическое распределение с параметром р (0<р<1), если она принимает натуральные значения  с вероятностями с вероятностями  , где q=1-p. , где q=1-p. o | X | | | | … | k | … | | P | p | qp | q2p | … | qk-1p | … | Очевидно, что вероятности появления значений 1,2,3… образуют геометрическую прогрессию с первым членом р и знаменателем q (0<q<1).  . .
Пример 1. Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель р=0,6. Найти вероятность того, что попадание произойдет при третьем выстреле. p=0,6; q=0,4; k=3.  . . Пример 2. Монета брошена два раза. Написать ряд распределения случайной величины X—числа выпадений «герба». Решение. Вероятность выпадения «герба» в каждом бросании монеты  , вероятность того, что «герб» не появится , вероятность того, что «герб» не появится  . . При бросании монеты «герб» может появится либо 2, либо 1, либо 0 раз. Т.е. возможные значения Х таковы: х1=0,х2=1, х3=2. Найдем вероятности этих возможных значений по формуле Бернулли: | |
 . Теорема 1. Пусть . Теорема 1. Пусть  —непрерывный случайный вектор. Тогда случайные величины —непрерывный случайный вектор. Тогда случайные величины  и и  —непрерывны, причем —непрерывны, причем  , ,  . Свойство 3. . Свойство 3.  , где , где  —множество из пространства IRn. o Говорят, что случайный вектор —множество из пространства IRn. o Говорят, что случайный вектор  имеет равномерное распределение в области имеет равномерное распределение в области  , если она непрерывна и имеет плотность. , если она непрерывна и имеет плотность.  Если множество Если множество   . o Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргумента Х. Теорема 2. Пусть случайная величина Х непрерывна с плотностью . o Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргумента Х. Теорема 2. Пусть случайная величина Х непрерывна с плотностью  , а случайная величина , а случайная величина  , где , где  —монотонная дифференцируемая функция, —монотонная дифференцируемая функция, | |
|  ; ;
 ; ;
 . .
Ряд распределения: 
Пример 3. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудут три негодных изделия(n-велико,p-мало). По условию n=5000, p=0,0002, k=3. По формуле Пуассона  , искомая вероятность , искомая вероятность  . . Наши рекомендации | |
 .
. по известным распределениям слагаемых. Такая задача часто встречается на практике. Например, если Х—погрешность показаний измерительного прибора (распределена равномерно), то возникает задача—найти закон распределения суммы погрешностей
по известным распределениям слагаемых. Такая задача часто встречается на практике. Например, если Х—погрешность показаний измерительного прибора (распределена равномерно), то возникает задача—найти закон распределения суммы погрешностей  .
.
 ,
,  .
.  ,
,  . Свойство 4.Функция F(x) непрерывна слева. (т.е.
. Свойство 4.Функция F(x) непрерывна слева. (т.е.  ). Свойство 5.Вероятность того, что значение случайной величины Х больше некоторого числа х, вычисляется по формуле.
). Свойство 5.Вероятность того, что значение случайной величины Х больше некоторого числа х, вычисляется по формуле.  . Достоверное событие {-∞<x<+∞} представим в виде двух несовместимых событий.
. Достоверное событие {-∞<x<+∞} представим в виде двух несовместимых событий.  . Найдем их вероятности
. Найдем их вероятности  . Поскольку вероятность достоверного события равна единице, то
. Поскольку вероятность достоверного события равна единице, то  . Отсюда
. Отсюда  . § 12. Дискретные случайные величины. o Случайная величина Х называется дискретной, если она принимает конечное либо счетное число значений, т.е. Ωх—конечно или счетно. o Законом распределения дискретной случайной величины Х называется совокупность пар чисел вида (хi, рi), где xi—возможные значения случайной величины, а pi—вероятности, с которыми случайная величина принимает эти значения, т.е.
. § 12. Дискретные случайные величины. o Случайная величина Х называется дискретной, если она принимает конечное либо счетное число значений, т.е. Ωх—конечно или счетно. o Законом распределения дискретной случайной величины Х называется совокупность пар чисел вида (хi, рi), где xi—возможные значения случайной величины, а pi—вероятности, с которыми случайная величина принимает эти значения, т.е.  , причем
, причем  . Простейшей формой задания дискретной случайной
. Простейшей формой задания дискретной случайной  .
. .
. ;
;  ;
;  .
. .
. можно сначала найти плотность распределения g(y) величины Y, а затем воспользоваться формулой:
можно сначала найти плотность распределения g(y) величины Y, а затем воспользоваться формулой:  .
. , то
, то  .
. в интервале (0, π/2); вне этого интервала р(х)=0. Найти математическое ожидание функции
в интервале (0, π/2); вне этого интервала р(х)=0. Найти математическое ожидание функции  .
. Ряд распределения можно изобразить графически. В этом случае по оси абсцисс откладывают значения xi, а по оси ординат—вероятности pi. Полученные точки соединяют отрезками и получают ломаную, которая является одной из форм задания закона распределения дискретной величины.
Ряд распределения можно изобразить графически. В этом случае по оси абсцисс откладывают значения xi, а по оси ординат—вероятности pi. Полученные точки соединяют отрезками и получают ломаную, которая является одной из форм задания закона распределения дискретной величины. с вероятностями
с вероятностями  .
. .
. ,
,  . Искомое распределение Y:
. Искомое распределение Y: ,
,  .
.

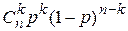

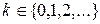 с вероятностями
с вероятностями  .
.

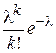
 , т.е. случайная величина Х имеет распределение Пуассона с параметром λ.
, т.е. случайная величина Х имеет распределение Пуассона с параметром λ. 
 . а) Пусть функция
. а) Пусть функция  возрастает. По определению
возрастает. По определению  .
.  Продифференцируем обе части. Справа получим:
Продифференцируем обе части. Справа получим:  , слева—
, слева—  , что и требовалось
, что и требовалось  . б) Пусть
. б) Пусть 

 . Продифференцировав обе части,
. Продифференцировав обе части,  . Покажем, как найти распределение функции случайного аргумента. Пусть аргумент Х—дискретная случайная величина
. Покажем, как найти распределение функции случайного аргумента. Пусть аргумент Х—дискретная случайная величина  .
. с вероятностями
с вероятностями  , где q=1-p.
, где q=1-p. .
. .
. , вероятность того, что «герб» не появится
, вероятность того, что «герб» не появится  .
. . Теорема 1. Пусть
. Теорема 1. Пусть  —непрерывный случайный вектор. Тогда случайные величины
—непрерывный случайный вектор. Тогда случайные величины  и
и  —непрерывны, причем
—непрерывны, причем  ,
,  . Свойство 3.
. Свойство 3.  , где
, где  —множество из пространства IRn. o Говорят, что случайный вектор
—множество из пространства IRn. o Говорят, что случайный вектор  имеет равномерное распределение в области
имеет равномерное распределение в области  , если она непрерывна и имеет плотность.
, если она непрерывна и имеет плотность.  Если множество
Если множество 
 . o Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргумента Х. Теорема 2. Пусть случайная величина Х непрерывна с плотностью
. o Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргумента Х. Теорема 2. Пусть случайная величина Х непрерывна с плотностью  , а случайная величина
, а случайная величина  , где
, где  —монотонная дифференцируемая функция,
—монотонная дифференцируемая функция,  ;
; ;
; .
.
 , искомая вероятность
, искомая вероятность  .
.