Матричная интерпретация алгоритма

Для n работников и работ, дана матрица n×n (матрица стоимости), задающая стоимость выполнения каждой работы каждым работником. Найти минимальную стоимость выполнения работ, такую что каждый работник выполняет ровно одну работу, а каждую работу выполняет ровно один работник.

В дальнейшем мы под назначением понимаем соответствие между работниками и работами, имеющее нулевую стоимость, после того как мы произвели трансформации, влияющие лишь на общую стоимость работ.

Прежде всего запишем задачу в матричной форме:

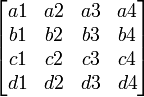
где a, b, c, d — работники, которые должны выполнить работы 1, 2, 3, 4. Коэффициенты a1, a2, a3, a4 обозначают стоимость выполнения работником «a» работ 1, 2, 3, 4 соответственно. Аналогичный смысл имеют остальные символы. Матрица квадратная, поэтому каждый работник может выполнить только одну работу.

Шаг 1

Уменьшаем элементы построчно. Находим наименьший из элементов первой строки (а1, а2, а3, а4), и вычитаем его из всех элементов первой строки. При этом хотя бы один из элементов первой строки обнулится. То же самое выполняем и для всех остальных строк. Теперь в каждой строке матрицы есть хотя бы один ноль. Иногда нулей уже достаточно, чтобы найти назначение. Пример показан в таблице. Красные нули обозначают назначенные работы.

	a2'		a4'
b1'	b2'	b3'
	c2'	c3'	c4'
d1'		d3'	d4'

При большом количестве нулей для поиска назначения (нулевой стоимости) можно использовать алгоритм нахождения максимального паросочетания двудольных графов, например алгоритм Хопкрофта-Карпа. Кроме того, если хотя бы в одном столбце нет нулевых элементов, то назначение невозможно.

Шаг 2

Часто на первом шаге нет назначения, как, например, в следующем случае:

	a2'	a3'	a4'
b1'	b2'	b3'
	c2'	c3'	c4'
d1'		d3'	d4'

Задача 1 может быть эффективно (за нулевую стоимость) выполнена как работником a, так и работником c, зато задача 3 не может быть эффективно выполнена никем.

В таких случаях мы повторяем шаг 1 для столбцов и вновь проверяем, возможно ли назначение.

Шаг 3

Во многих случаях мы достигнем желаемого результата уже после шага 2. Но иногда это не так, например:

	a2'	a3'	a4'
b1'	b2'	b3'
	c2'	c3'	c4'
d1'			d4'

Если работник d выполняет работу 2, некому выполнять работу 3, и наоборот.

В таких случаях мы выполняем процедуру, описанную ниже.

Сначала, используя любой алгоритм поиска максимального паросочетания в двудольном графе, назначаем как можно больше работ тем работникам, которые могут их выполнить за нулевую стоимость. Пример показан в таблице, назначенные работы выделены красным.

	a2'	a3'	a4'
b1'	b2'	b3'
	c2'	c3'	c4'
d1'			d4'

Отметим все строки без назначений (строка 1). Отметим все столбцы с нулями в этих строках (столбец 1). Отметим все строки с «красными» нулями в этих столбцах (строка 3). Продолжаем, пока новые строки и столбцы не перестали отмечаться.

×
	a2'	a3'	a4'	×
b1'	b2'	b3'
	c2'	c3'	c4'	×
d1'			d4'

Теперь проводим линии через все отмеченные столбцы и неотмеченные строки.

×
	a2'	a3'	a4'	×
b1'	b2'	b3'
	c2'	c3'	c4'	×
d1'			d4'

Все эти действия преследовали лишь одну цель: провести наименьшее количество линий (вертикалей и горизонталей), чтобы покрыть все красные нули. Можно было воспользоваться любым другим методом вместо описанного.

Шаг 4

Из непокрытых линиями элементов матрицы (в данном случае это a2', a3', a4', c2', c3', c4') найти наименьший. Вычесть его из всех не отмеченных строк и прибавить ко всем пересечениям отмеченных строк и столбцов. Так, например, если наименьший элемент из перечисленных равен а2', мы получим

×
		a3'-а2'		a4'-a2'	×
b1'+a2'	b2'	b3'
	c2'-а2'	c3'-а2'		c4'-а2'	×
d1'+a2'				d4'

Повторять процедуру (шаги 1-4) до тех пор, пока назначение не станет возможным.

Реализация на python.

В листинге 3 приводится пример реализации решения примера, описанного выше, на языке программирования python.

Листинг 3.

def improveLabels(val):

""" change the labels, and maintain minSlack.

"""

for u in S:

lu[u] -= val

for v in V:

if v in T:

lv[v] += val

else:

minSlack[v][0] -= val

def improveMatching(v):

""" apply the alternating path from v to the root in the tree.

"""

u = T[v]

if u in Mu:

improveMatching(Mu[u])

Mu[u] = v

Mv[v] = u

def slack(u,v): return lu[u]+lv[v]-w[u][v]

def augment():

""" augment the matching, possibly improving the lablels on the way.

"""

while True:

# select edge (u,v) with u in S, v not in T and min slack

((val, u), v) = min([(minSlack[v], v) for v in V if v not in T])

assert u in S

if val>0:

improveLabels(val)

# now we are sure that (u,v) is saturated

assert slack(u,v)==0

T[v] = u # add (u,v) to the tree

if v in Mv:

u1 = Mv[v] # matched edge,

assert not u1 in S

S[u1] = True # ... add endpoint to tree

for v in V: # maintain minSlack

if not v in T and minSlack[v][0] > slack(u1,v):

minSlack[v] = [slack(u1,v), u1]

else:

improveMatching(v) # v is a free vertex

return

def maxWeightMatching(weights):

""" given w, the weight matrix of a complete bipartite graph,

returns the mappings Mu : U->V ,Mv : V->U encoding the matching

as well as the value of it.

"""

global U,V,S,T,Mu,Mv,lu,lv, minSlack, w

w = weights

n = len(w)

U = V = range(n)

lu = [ max([w[u][v] for v in V]) for u in U] # start with trivial labels

lv = [ 0 for v in V]

Mu = {} # start with empty matching

Mv = {}

while len(Mu)<n:

free = [u for u in V if u not in Mu] # choose free vertex u0

u0 = free[0]

S = {u0: True} # grow tree from u0 on

T = {}

minSlack = [[slack(u0,v), u0] for v in V]

augment()

# val. of matching is total edge weight

val = sum(lu)+sum(lv)

return (Mu, Mv, val)

# a small example

#print maxWeightMatching([[1,2,3,4],[2,4,6,8],[3,6,9,12],[4,8,12,16]])

# read from standard input a line with n

# then n*n lines with u,v,w[u][v]

n = 3 #Размер матрицы

w = [[1, 2, 4], #Матрица весов

[2, 5, 3],

[6, 7, 8]]

print(maxWeightMatching(w))

Входные данные:

n = 3 #Размер матрицы

w = [[1, 2, 4], #Матрица весов

[2, 5, 3],

[6, 7, 8]]

Выходные данные:

({0: 2, 1: 1, 2: 0}, {0: 2, 1: 1, 2: 0}, 15)

Вывод.

Матричное представление графов – наиболее универсальное представление графов в памяти эвм, для дальнейшей их обработки и решения разного рода задач.

Список использованной литературы.

Литература:

Свами М., Тхуласираман К. Графы, сети и алгоритмы. М.: Мир, 1984

Хаггарти Р. Дискретная математика для программистов Москва: Техносфера, 2003 г. - 320с.

Интернет-ресурсы:

Википедия - свободная общедоступная мультиязычная универсальная интернет-энциклопедия, реализованная на принципах Вики. / http://wikipedia.org (Дата обращения 23.12.2013)

Приложение.

Ниже приведены исходные коды всех примеров, проденмонстрированных выше.

#Example1.py

from operator import itemgetter

import networkx as nx

import matplotlib.pyplot as plt

G = nx.Graph()

G.add_edge(1,2);

G.add_edge(2,3);

G.add_edge(3,1);

nx.draw(G, node_color = 'b', width = 5, with_labels = False)

plt.show()

#deijkstra.py

import networkx as nx

import matplotlib.pyplot as plt

G = nx.DiGraph()

G.add_nodes_from(range(1, 7))

for i in range(1,10):

G.add_edge(i, i-1)

for i in range(1,10):

if(i+5<10):

G.add_edge(i, i+5, weight = i*0.5+2)

nx.draw(G, node_color = 'm', font_color = 'w')

plt.show()

print(nx.dijkstra_path(G, 2, 8))

#mankres.py

#!/usr/bin/python

# Kuhn-Munkres, The hungarian algorithm. Complexity O(n^3)

# Computes a max weight perfect matching in a bipartite graph

# for min weight matching, simply negate the weights.

""" Global variables:

n = number of vertices on each side

U,V vertex sets

lu,lv are the labels of U and V resp.

the matching is encoded as

- a mapping Mu from U to V,

- and Mv from V to U.

The algorithm repeatedly builds an alternating tree, rooted in a

free vertex u0. S is the set of vertices in U covered by the tree.

For every vertex v, T[v] is the parent in the tree and Mv[v] the

child.

The algorithm maintains minSlack, s.t. for every vertex v not in

T, minSlack[v]=(val,u1), where val is the minimum slack

lu[u]+lv[v]-w[u][v] over u in S, and u1 is the vertex that

realizes this minimum.

Complexity is O(n^3), because there are n iterations in

maxWeightMatching, and each call to augment costs O(n^2). This is

because augment() makes at most n iterations itself, and each

updating of minSlack costs O(n).

"""

def improveLabels(val):

""" change the labels, and maintain minSlack.

"""

for u in S:

lu[u] -= val

for v in V:

if v in T:

lv[v] += val

else:

minSlack[v][0] -= val

def improveMatching(v):

""" apply the alternating path from v to the root in the tree.

"""

u = T[v]

if u in Mu:

improveMatching(Mu[u])

Mu[u] = v

Mv[v] = u

def slack(u,v): return lu[u]+lv[v]-w[u][v]

def augment():

""" augment the matching, possibly improving the lablels on the way.

"""

while True:

# select edge (u,v) with u in S, v not in T and min slack

((val, u), v) = min([(minSlack[v], v) for v in V if v not in T])

assert u in S

if val>0:

improveLabels(val)

# now we are sure that (u,v) is saturated

assert slack(u,v)==0

T[v] = u # add (u,v) to the tree

if v in Mv:

u1 = Mv[v] # matched edge,

assert not u1 in S

S[u1] = True # ... add endpoint to tree

for v in V: # maintain minSlack

if not v in T and minSlack[v][0] > slack(u1,v):

minSlack[v] = [slack(u1,v), u1]

else:

improveMatching(v) # v is a free vertex

return

def maxWeightMatching(weights):

""" given w, the weight matrix of a complete bipartite graph,

returns the mappings Mu : U->V ,Mv : V->U encoding the matching

as well as the value of it.

"""

global U,V,S,T,Mu,Mv,lu,lv, minSlack, w

w = weights

n = len(w)

U = V = range(n)

lu = [ max([w[u][v] for v in V]) for u in U] # start with trivial labels

lv = [ 0 for v in V]

Mu = {} # start with empty matching

Mv = {}

while len(Mu)<n:

free = [u for u in V if u not in Mu] # choose free vertex u0

u0 = free[0]

S = {u0: True} # grow tree from u0 on

T = {}

minSlack = [[slack(u0,v), u0] for v in V]

augment()

# val. of matching is total edge weight

val = sum(lu)+sum(lv)

return (Mu, Mv, val)

# a small example

#print maxWeightMatching([[1,2,3,4],[2,4,6,8],[3,6,9,12],[4,8,12,16]])

# read from standard input a line with n

# then n*n lines with u,v,w[u][v]

n = 3 #Размер матрицы

w = [[1, 2, 4], #Матрица весов

[2, 5, 3],

[6, 7, 8]]

print(maxWeightMatching(w))

#tsp.py

import networkx as nx

import matplotlib.pyplot as plt

import numpy

G = nx.Graph();

for i in range(1,6):

G.add_node(i)

G.add_edge(1, 2, node_color = 'm', weight = 2) # Параметр weight отвечает за вес ребра

G.add_edge(1, 3, node_color = 'm', weight = 1)

G.add_edge(1, 4, node_color = 'm', weight = 20)

G.add_edge(1, 5, node_color = 'm', weight = 10)

G.add_edge(1, 6, node_color = 'm', weight = 15)

G.add_edge(5, 4, node_color = 'm', weight = 1)

G.add_edge(1, 6, node_color = 'm', weight = 10)

G.add_edge(6, 1, node_color = 'm', weight = 4)

G.add_edge(2, 3, node_color = 'm', weight = 10)

G.add_edge(2, 5, node_color = 'm', weight = 5)

G.add_edge(2, 6, node_color = 'm', weight = 20)

G.add_edge(3, 6, node_color = 'm', weight = 6)

G.add_edge(4, 2, node_color = 'm', weight = 15)

G.add_edge(4, 3, node_color = 'm', weight = 40)

G.add_edge(5, 6, node_color = 'm', weight = 10)

G.add_edge(3, 5, node_color = 'm', weight = 3)

nx.draw(G) #Отрисовка графа

plt.show()

adjacency_matrix = nx.adjacency_matrix(G)

print('Матрица стоимости')

print(adjacency_matrix) #Вывод матрицы весов

print(nx.shortest_path(G, 1, 4)) #Вывод самого короткого пути

print(nx.dijkstra_path(G, 1, 4)) #Вывод самого "выгодного" пути