Применение методов при решении задач

КУРСОВАЯ РАБОТА

по дисциплине «Термодинамика и статическая физика»

Методы решения задач магнитостатики

ОГТИ (филиал) ГОУ ОГУ 050100.62014100

Руководитель работы _________________Б.Ф. Костромин "_____"_________________ 2015 г. Исполнитель Студент гр11ПО (б) Физ ___________________ А. В. Горшков "_____"_________________2015 г.

Орск 2015

Аннотация

В данной курсовой работе содержатся методы решения уравнения Лапласа при заданных граничных условиях на тех или иных поверхностях изучаются в соответствующем разделе математической физики, и в нашу цель не входит полное их изложение. Мы ограничимся здесь указанием лишь некоторых более простых приемов и решением ряда типичных задач, имеющих самостоятельный интерес.

Целью работы является формирование компетентности в сфере познавательной деятельности через использование исторического материала в курсе физики.

Данная работа состоит из 45 страниц и включает в себя четыре главы, введение, заключение и список использованных источников.

Во введении изложена цель работы, актуальность выбранной темы, а так же поставлен ряд задач, которые предстоит решить в ходе анализа данной темы.

Первая глава посвящена рассмотрению теоретических аспектов историзма в обучении физике.

Во второй главе представлена реализация принципа историзма в обучении физике.

В третьей главе

В четвертой главе

В заключении описаны полученные результаты проделанной работы.

Содержание

Введение

1 Методы решения задач магнитостатики

1.1 Метод изображений

1.2 Метод инверсии

1.3 Метод конформного отображения

1.4 Задача о клине

1.5 Задачи и решения

2 Применение методов при решении задач

Заключение

Список использованных источников

Методы решения задач магнитостатики

Метод изображений

Метод инверсии

Метод конформного отображения

Задача о клине

Задачи и решения

Применение методов при решении задач

Общие методы решения уравнения Лапласа при заданных граничных условиях на тех или иных поверхностях изучаются в соответствующем разделе математической физики, и в нашу цель не входит полное их изложение. Мы ограничимся здесь лишь указанием некоторых более простых приемов и решением ряда типичных задач, имеющих самостоятельный интерес.

2.1 Метод изображений.

Определение поля, создаваемого точечным зарядом , расположенным вне проводящей среды, заполняющей полупространство, является простейшим примером применения так называемого метода изображений. Идея этого метода состоит в подборе таких дополнительных фиктивных точечных зарядов, которые вместе с данными зарядами создавали бы поле, для которого поверхность заданного проводника совпадала бы с одной из эквипотенциальных поверхностей поля.

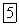В данном случае это достигается введением фиктивного заряда расположенного в точке, представляющей собой зеркальное отражение точки в граничной плоскости проводящей среды. Потенциал поля заряда и его «изображения» равен

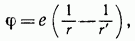
где — расстояния точки наблюдения от зарядов . На граничной плоскости и потенциал имеет постоянное значение так что необходимое граничное условие действительно выполняется и (3,1) дает решение поставленной задачи. Отметим, что заряд притягивается к проводнику с силой (сила изображения), а энергия взаимодействия равна — .

Распределение на граничной плоскости поверхностных зарядов, индуцированных точечным зарядом , дается формулой

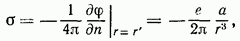
где а — расстояние от заряда до плоскости. Легко убедиться в том, что полный заряд на этой плоскости равен

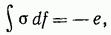
как и должно быть.

Общий заряд, индуцированный посторонними зарядами на первоначально не заряженном изолированном проводнике, разумеется, остается равным нулю. Поэтому, если в данном случае проводящая среда (в действительности — проводник больших размеров) изолирована, то надо представлять себе, что одновременно с зарядом индуцируется заряд который, однако, будучи распределен по поверхности большого тела, имеет исчезающую плотность.

Далее, рассмотрим более сложную задачу о поле, создаваемом точечным зарядом , находящимся вблизи шарового проводника. Для решения этой задачи воспользуемся следующим результатом, который легко проверить непосредственными вычислениями. Потенциал поля, создаваемого двумя точечными зарядами ,

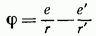
обращается в нуль на сферической поверхности радиуса R, центр которой лежит на продолжении прямой, соединяющей точки не, на расстоянии от этих точек, причем удовлетворяют равенствам .

Предположим сначала, что шаровой проводник поддерживается при постоянном потенциале (шар заземлен).

Тогда поле, создаваемое вне шара точечным зарядом , находящимся на расстоянии l от центра шара (в точке А на рис. 1), будет совпадать с полем, создаваемым системой двух зарядов данным зарядом и фиктивным зарядом , помещенным внутри шара (точка А) на расстоянии Г от его центра, причем

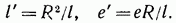
Потенциал этого поля

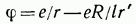
(см. рис. 1). На поверхности шара индуцируется при этом отличный от нуля полный заряд, равный Энергия взаимодействия заряда с шаром равна

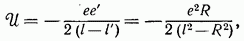
и заряд притягивается к шару с силой

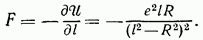
Если же проводящая сфера поддерживается при равном нулю полном заряде (изолированный незаряженный шар), то надо ввести еще один фиктивный заряд таким образом, чтобы полный индуцированный на поверхности шара заряд оказался равным нулю, причем не должно нарушаться постоянство потенциала на этой поверхности. Это достигается помещением заряда в центр шара. Потенциал искомого поля определится тогда формулой

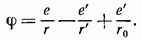
Энергия взаимодействия в этом случае будет

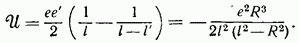
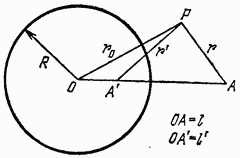
Рис. 1.

Наконец, если заряд находится в сферической полости в проводящей среде (в точке А, рис. 1), то поле внутри полости совпадает с полем, которое создавалось бы зарядом и его «изображением» в точке А вне сферы (независимо от того, заземлен проводник или изолирован):

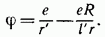
Метод инверсии. Существует простой метод, который в ряде случаев позволяет по известному решению одной электростатической задачи находить решение другой задачи. Основанием этого метода является инвариантность уравнения Лапласа по отношению к определенному преобразованию переменных.

В сферических координатах уравнение Лапласа имеет вид

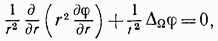
где посредством обозначена угловая часть оператора Лапласа. Легко убедиться в том, что это уравнение сохраняет свою форму, если вместо переменной ввести новую переменную согласно

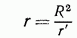
(преобразование инверсии) и одновременно заменить неизвестную функцию согласно

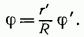
Здесь - некоторая постоянная с размерностью длины (радиус инверсии). Таким образом, если функция удовлетворяет уравнению Лапласа, то функция

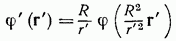
тоже есть решение этого уравнения.

Предположим, что нам известно решение задачи об электростатическом поле, создаваемом некоторой системой проводников, которые находятся при одном и том же потенциале и системой точечных зарядов. Потенциал обычно определяют так, чтобы он обращался в нуль на бесконечности. Здесь, однако, мы определим так, чтобы на бесконечности эта функция стремилась к тогда на проводниках

Выясним теперь, какая электростатическая задача будет решаться преобразованной функцией (3,11). Прежде всего, меняются фигуры всех протяженных проводников и их взаимное расположение. Граничное условие постоянства потенциала на поверхности проводников автоматически выполняется, так как при будет и Далее, меняются расположение и величины всех точечных зарядов. Заряд, находящийся в точке переходит в точку и приобретает величину , которую можно определить следующим образом. При потенциал обращается в бесконечность по закону , где . С другой стороны, дифференцируя соотношение , найдем, что абсолютные значения малых разностей связаны друг с другом соотношением

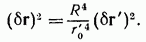
Поэтому при функция стремится к бесконечности по закону

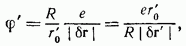
соответствующему заряду

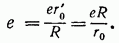
Наконец, рассмотрим поведение функции вблизи начала координат. Точке соответствует . Но при функция стремится к Поэтому при функция обращается в бесконечность по закону

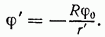
Это значит, что в точке находится заряд

Укажем, как преобразуются при инверсии некоторые геометрические фигуры. Сферическая поверхность радиуса а с центром в точке дается уравнением

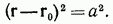
Произведя инверсию, получим уравнение

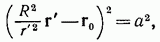
которое после умножения на и перегруппировки членов может быть приведено к виду где

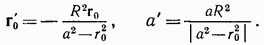
Таким образом, мы снова получаем сферу другого радиуса а и с центром в точке Если первоначальная сфера проходила через начало координат ), то в этом случае сфера преобразуется в плоскость, перпендикулярную к направлению и проходящую на расстоянии

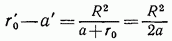
от начала координат.