Метод конечных элементов. Как мы уже говорили, МКЭ – проекционный метод со специальными координатными
Как мы уже говорили, МКЭ – проекционный метод со специальными координатными функциями. Выберем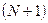 
координатную функцию для решения задачи (1.4), (1.5). Каждому узлу сутки 
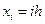поставим в соответствие непрерывную кусочно-линейную функцию 
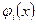, равную 1 в узле 
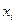и нулю во всех прочих узлах. Это известные сегодня всем функции, изображенные на рис.3.
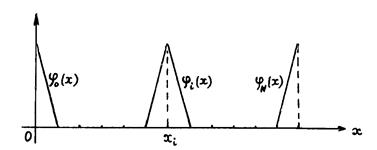
Рис.3. Кусочно-линейные координатные функции
Функции 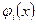удобно представить через одну стандартную функцию 
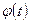, заданную на всей вещественной оси 
:
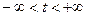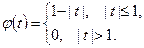
Тогда, очевидно,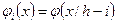 
, 
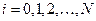. Пусть теперь 
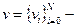сеточная функция. Произведя линейную интерполяцию по значениям 
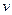в узлах сетки, получим непрерывную кусочно-линейную функцию 
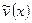, заданную при всех значениях 
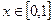. Для функции 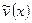имеет место представление
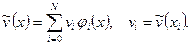
Множество непрерывных, линейных на каждом интервале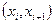 
функций образует подпространство пространства 
, функции 
, 
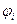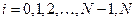, образуют в этом подпространстве базис. Обозначим его через 
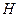. Множество непрерывных, кусочно-линейных функций, равных нулю на концах отрезка образует подпространство пространства 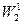с базисом, состоящим из , 
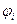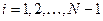. Это подпространство обозначим через 
.
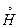Приближенное решение задачи (1.4), (1.5) ищем в виде
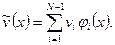
Очевидно, что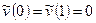 
. Искомые коэффициенты 
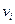определяются как решение системы
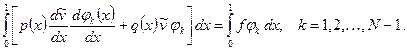(1.21)
При кусочно-линейных координатных функциях эта система представляет собой систему уравнений МКЭ. Заметим, что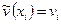 
. Неизвестными, следовательно, являются значения искомой функции в узлах сетки.
Покажем, что система (1.21) близка к системе разностных уравнений (1.18). Эта близость существенным образом опирается на следующее важное свойство координатных функций.
Каждая координатная функция ортогональна всем остальным кроме некоторого конечного числа (в данном случае это число равно 2), не зависящего от общего числа координатных функций, т.е. от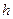 
. Это общее и весьма важное свойство координатных функций МКЭ. Как понимается эта ортогональность? Рассмотрим следующую билинейную форму:
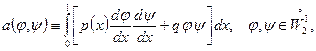
определенную на функциях из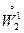 
. При условии, что 
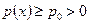и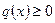 
, эта билинейная форма обладает всеми свойствами скалярного произведения. Каковы эти свойства: линейность по каждому аргументу, симметрия и вот, пожалуй, то свойство, которое нуждается в проверке: из равенства 
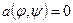следует, что 
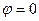. Покажем это. Имеют место неравенства
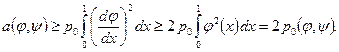(1.22)
Первое из этих неравенств очевидно, второе докажем. Так как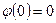 
, то
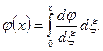
Возводя обе части этого равенства в квадрат и используя известное неравенство Коши – Буняковского
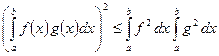или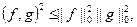 
получим
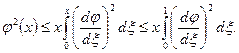
Следовательно:
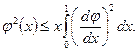
Интегрируя обе части этого неравенства по 
в пределах от 0 до 1, получим
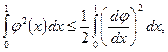
так что неравенство (1.22) справедливо. Тогда из следует, что
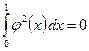
и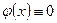 
.
Итак,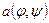 
обладает всеми свойствами скалярного произведения. Упомянутая выше ортогональность как раз и важна в этом скалярном произведении, так как с его помощью вычисляются коэффициенты матрицы системы сеточных уравнений (1.21).
Поскольку 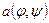можно рассматривать как скалярное произведение, то 
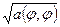определяет в 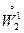норму. Введем обозначение
|| 
|| 
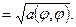
Эту норму называют энергетической нормой краевой задачи (1.4), (1.5). Она эквивалентна норме пространства 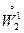. Действительно:
|| || 
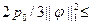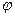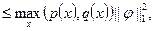
следовательно,
|| || 
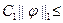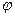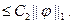
Это неравенство и означает, что нормы эквивалентны.
Система сеточных уравнений (1.21) не более, чем трехдиагональна. В самом деле
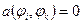при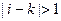 
,
т.е.
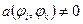только при 
,
, 
;
; 
.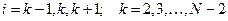
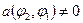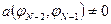
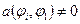
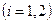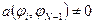
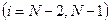