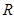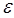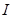Амплитудно-частотная и фазово-частотная характеристики
Департамент по авиации
Министерства транспорта и коммуникаций Республики Беларусь
УО «Белорусская государственная академия авиации»
Кафедра естественнонаучных дисциплин
КУРСОВАЯ РАБОТА
Тема: Расчет частотных и фазовых характеристик четырехполюсника
По дисциплине: «Высшая математика»
Специальность: «Техническая эксплуатация авиационного оборудования»
Выполнил:
студент 3 курса
учебной группы 3ПВ147
учебный шифр 14716
Копчинский В.А
Руководитель И. В. Кисель
Содержание
Введение……………………………………………………………......................3
1.Уравнения Максвела……………………………………………………………4
2.Уравнения Кирхгофа для переменных токов и
напряжений в линейных электрических цепях…………………………………7
3.Вывод основных соотношений четырехполюсника,содержащего активные и реактивные элементы и усилитель напряжения...……………………………13
4.Амплитудно-частотная и фазово-частотная характеристики….….…........18
5 .Расчетная часть параметров четырехполюсника……………......................20
6. Расчетные формулы………………………………………………………..21
7. Таблицы расчетов…………………………………………………………...23
8. Графическая часть ………………………………………………………….26
Вывод …………………………………………………………………………....32
Список использованных источников……………………..…………………...33
Введение
Четырехполюсником называется часть схемы электрической цепи между двумя парами точек, к которым присоединены две ветви.
Зажимы, к которым присоединяется ветвь с источником энергии, называются входными, а зажимы, к которым присоединяется приемник,-выходными.
На одной или на обеих парах разомкнутых зажимов линейного активного четырехполюсника обнаруживается напряжение. На разомкнутых зажимах отключенного от источника пассивного четырехполюсника напряжение отсутствует.
Теория четырехполюсников позволяет, пользуясь некоторыми обобщенными параметрами, связать между собой напряжения и токи на входе и на выходе, не производя расчетов токов и напряжений в схеме самого четырехполюсника.
Если ставится задача исследовать изменение режима одной ветви при изменении электрических характеристик другой ветви, применяется метод четырехполюсника. Например, при исследовании линий передач, трансформаторов, асинхронных двигателей, усилителей, преобразователей и других устройств.
Цель работы: исследовать устойчивость системы четырехполюсника. Для этого нужно определитьамплитудно-частотную и фазово-частотную характеристики, абсолютную величину входного и выходного сопротивлений четырехполюсника для одной из частот 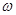 в области максимума коэффициента усиления,построить амплитудно-частотную характеристику коэффициента усиления в двойном логарифмическом масштабе, построить фазово-частотную характеристику в полулогарифмическом масштабе.
в области максимума коэффициента усиления,построить амплитудно-частотную характеристику коэффициента усиления в двойном логарифмическом масштабе, построить фазово-частотную характеристику в полулогарифмическом масштабе.
Уравнения Максвелла.
Базовой математической моделью для описания всего многообразия электрических, магнитных и электромагнитных явлений, включая распространение электромагнитных волн, являются уравнения Максвелла, которые в дифференциальной форме имеют вид:

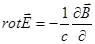 , (1)
, (1)
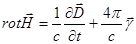 , (2)
, (2)
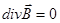 , (3)
, (3)
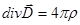 , (4)
, (4)
где: с – скорость света = 3∙1010 (см/сек);
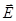 и
и 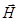 - напряженности электрического и магнитного полей соответственно(А/м);
- напряженности электрического и магнитного полей соответственно(А/м); 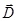 и
и 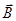 - вектора электрической(Кл/м2) и магнитной(Тл) индукции полей;
- вектора электрической(Кл/м2) и магнитной(Тл) индукции полей; 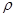 - плотность электрического заряда;
- плотность электрического заряда; 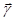 - плотность электрического тока,
- плотность электрического тока, 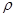 и
и 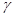 связаны соотношением:
связаны соотношением:
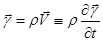 . (5)
. (5)
Величины 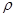 и
и 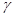 следует понимать как усреднение по физически малому объему
следует понимать как усреднение по физически малому объему 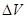 :
:
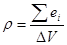 ;
; 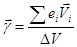 , (6)
, (6)
где 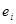 и
и 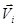 - величина и объем
- величина и объем 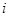 -го заряда.
-го заряда.
Суммирование проводится по всем зарядам, содержащимся в объеме 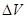 .
.
В модели, учитывающей реальное дискретное распределение и точечный характер зарядов, следует использовать выражение:
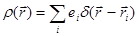 , (7)
, (7)
где 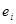 и
и 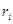 - величина и радиус-вектор
- величина и радиус-вектор 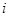 -го заряда системы,
-го заряда системы, 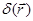 - трехмерная
- трехмерная 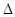 функция, которая относится к классу обобщенных функций и формально задается соотношением:
функция, которая относится к классу обобщенных функций и формально задается соотношением:
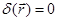 ,
, 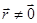 , (8)
, (8)
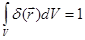 , интегрирование проводят по всему пространству.
, интегрирование проводят по всему пространству.
В интегральной форме, более удобной для ряда приложений, уравнения Максвелла имеют вид:
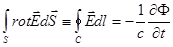 , (9)
, (9)
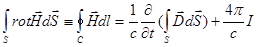 , (10)
, (10)
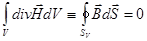 , (11)
, (11)
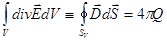 , (12)
, (12)
где (по определению) :
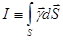 , (13)
, (13)
- электрический ток, протекающий через поверхность 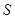 ;
;
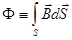 , (14)
, (14)
- магнитный поток, пронизывающий поверхность 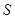 ;
;
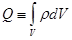 , (15)
, (15)
- суммарный заряд, находящийся в объеме 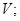
С - замкнутый контур, на который опирается поверхность 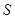 ;
;
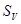 - замкнутая поверхность, ограниченная объемом
- замкнутая поверхность, ограниченная объемом 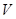 .
.
Уравнения Максвелла позволяют, если заданы пространственные распределения плотности электрического заряда 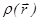 и плотности тока
и плотности тока 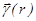 либо заданы положения и скорости (
либо заданы положения и скорости ( 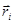 и
и 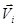 ) всех точечных зарядов системы, определить пространственные распределения напряженности магнитного и электрического полей.
) всех точечных зарядов системы, определить пространственные распределения напряженности магнитного и электрического полей.
Сила, которая действует на точечный заряд ( 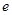 ) со стороны электрических и магнитных полей (сила Лоренца), определяется соотношением:
) со стороны электрических и магнитных полей (сила Лоренца), определяется соотношением:
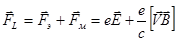 , (16)
, (16)
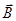 - вектор магнитной индукции;
- вектор магнитной индукции;
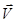 - скорость заряда.
- скорость заряда.
Уравнения Максвелла ( 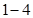 ) совместно с уравнениями (
) совместно с уравнениями ( 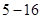 ) и системой уравнений механики (
) и системой уравнений механики ( 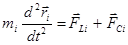 , где
, где 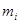 - масса
- масса 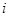 -го заряда;
-го заряда; 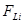 - сила Лоренца, действующая на него со стороны электрического поля;
- сила Лоренца, действующая на него со стороны электрического поля; 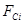 - силы другой природы, действующие на этот же заряд) образуют замкнутую систему уравнений , позволяющую в рамках классической физики описывать поведение любой заданной системы зарядов.
- силы другой природы, действующие на этот же заряд) образуют замкнутую систему уравнений , позволяющую в рамках классической физики описывать поведение любой заданной системы зарядов.
2. Уравнение Кирхгофа для переменных токов и напряжений в линейных электрических цепях.
 Базовыми уравнениями для описания процессов в электрических цепях с изменяющимися во времени токами (
Базовыми уравнениями для описания процессов в электрических цепях с изменяющимися во времени токами ( 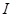 ) и напряжениями (
) и напряжениями ( 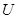 ) являются уравнения Максвелла в интегральной форме (1.9 – 1.12).
) являются уравнения Максвелла в интегральной форме (1.9 – 1.12).
Рассмотрим электрическую цепь, содержащую источник переменной ЭДС ( 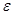 ), активное сопротивление (
), активное сопротивление ( 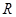 ), емкость (
), емкость ( 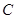 ), индуктивность (
), индуктивность ( 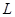 ).
).
|
|
| ||||||
|

|
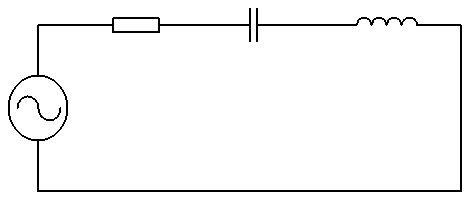
Рисунок 1 Схема электрической цепи, содержащей источник переменной ЭДС 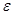 (В) , активное сопротивление
(В) , активное сопротивление 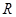 (Ом), емкость
(Ом), емкость 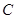 (Ф), индуктивность
(Ф), индуктивность 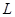 (Гн).
(Гн).
Представление любой электрической цепи в виде набора дискретных элементов есть приближенная модель , имеющая определенные границы своего применения, в частности, по номинальным значениям токов и напряжений и по характерным частотам токов и напряжений.
Любой участок цепи обладает как индуктивным, так и емкостным сопротивлениями.
Элементы цепи (сопротивления, индуктивности, емкости, проводники) конструируются таким образом, чтобы наилучшим образом выполнять определенную именно для него функцию.
Фундаментальное ограничение на такую модель связано с условием квазистационарности:
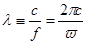 >>
>> 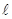 , (17)
, (17)
где 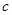 - скорость света;
- скорость света; 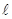 - характерные (максимальные) размеры контура;
- характерные (максимальные) размеры контура; 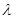 - длина волны электромагнитного излучения, соответствующая частоте изменения электрического поля
- длина волны электромагнитного излучения, соответствующая частоте изменения электрического поля 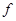 .
.
При 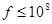 сек-1 :
сек-1 :
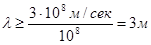 >>
>> 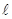 .
.
То есть, запас применимости модели, как по рабочим частотам, так и по габаритам радиотехнических устройств достаточно велик.
Рассмотрим в качестве замкнутого контура С нашу цепь. Для этой цепи интеграл по контуру разбивается на участки:
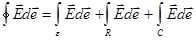 . (18)
. (18)
Элементы цепи по определению обладают свойствами:
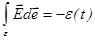 , (19)
, (19)
(электрическое поле внутри источника ЭДС противоположно по направлению полю вне источника);
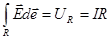 , (20)
, (20)
(закон Ома);
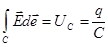 , (21)
, (21)
(связь между зарядом и напряжением по емкости);
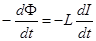 , (22)
, (22)
(по определению индуктивности);
Таким образом, вместо (18) с учетом (19) - (22) получаем
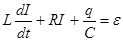 . (23)
. (23)
Если учесть, что:
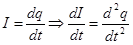 , (24)
, (24)
то получаем дифференциальное уравнение второго порядка (линейное с постоянными коэффициентами) для неизвестной функции 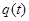 с заданной правой частью
с заданной правой частью 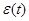 :
:
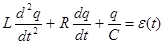 . (25)
. (25)
Общее решение этого уравнения имеет вид:
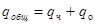 , (26)
, (26)
где 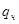 - частное решение уравнения (25);
- частное решение уравнения (25);
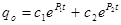 - общее решение однородного уравнения
- общее решение однородного уравнения
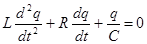 , (27)
, (27)
содержащее произвольные константы 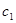 и
и 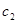 ;
;
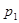 и
и 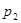 - корни характеристического уравнения
- корни характеристического уравнения
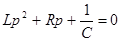 , (28)
, (28)
Уравнение (27) формально получается из уравнения (28), если заменить:
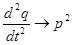
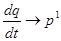
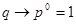 .
.
Решая задачу Коши при заданных начальных условиях
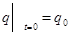 ,
, 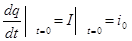 , (29)
, (29)
получаем единственное решение 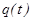 и
и 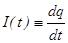 .
.
Корни 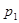 и
и 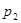 точно как и постоянные
точно как и постоянные 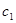 и
и 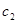 могут быть комплексными. Такое расширение решения уравнения (29) на комплексную область позволяет получить математически более удобную и компактную форму записи.
могут быть комплексными. Такое расширение решения уравнения (29) на комплексную область позволяет получить математически более удобную и компактную форму записи.
Физический смысл имеют только действительные заряды и токи, поэтому в результате решения задачи Коши функция 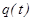 всегда получается действительной.
всегда получается действительной.
Исследуем вопрос об устойчивости системы, описываемой уравнением типа ( 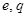 ), если хотя бы один из корней
), если хотя бы один из корней 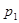 и
и 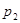 имеет положительную действительную часть:
имеет положительную действительную часть:
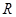
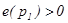 или
или 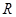
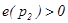 , то при любых малых
, то при любых малых 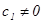 и
и 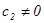 ,
, 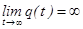 . Так как в реальных системах из-за наличия шумов всегда существуют моменты времени, когда
. Так как в реальных системах из-за наличия шумов всегда существуют моменты времени, когда 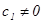 и
и 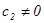 , то в такой системе токи начнут неограниченно возрастать и уравнение типа (
, то в такой системе токи начнут неограниченно возрастать и уравнение типа ( 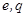 )перестанет описывать процессы в этой системе.
)перестанет описывать процессы в этой системе.
В рассмотренном случае при 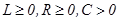 ,
, 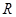
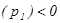 и
и 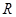
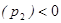 . Решение всегда устойчиво, но в случае более сложных цепей, содержащих не только пассивные элементы, но и активные (усилители тока или напряжения), условия устойчивости могут выполняться не всегда. Если внешнее воздействие гармоническое, то есть
. Решение всегда устойчиво, но в случае более сложных цепей, содержащих не только пассивные элементы, но и активные (усилители тока или напряжения), условия устойчивости могут выполняться не всегда. Если внешнее воздействие гармоническое, то есть
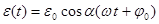 , (30)
, (30)
то решение уравнения (25), соответствующее установившемуся режиму ( 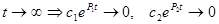 ), может быть найдено с помощью следующего приема.
), может быть найдено с помощью следующего приема.
Рассмотрим
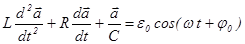 , (31)
, (31)
а также уравнение
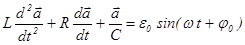 , (32)
, (32)
умножая уравнение (32) на мнимую единицу и складывая его почленно с уравнением (31) , преобразовав правую часть по формуле Эйлера (еix=cosx+iˑsinx),получаем уравнение:
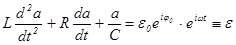 , (33)
, (33)
где 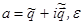 есть комплексный аналог гармонического
есть комплексный аналог гармонического
воздействия (30).
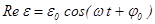 . (34)
. (34)
Таким образом, решаем уравнение (33) и затем, находя действительную часть 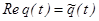 , получаем действительное решение интересующей нас задачи. Ищем решение (33) в виде:
, получаем действительное решение интересующей нас задачи. Ищем решение (33) в виде:
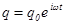 , (35)
, (35)
тогда 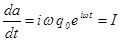
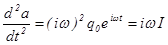 ;
; 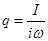 , и тогда с учетом этих соотношений из уравнения (33) получаем
, и тогда с учетом этих соотношений из уравнения (33) получаем
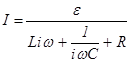 . (36)
. (36)
Это есть комплексный аналог закона Ома, если формально рассматривать индуктивность, емкость и активное сопротивление как комплекс сопротивлений:
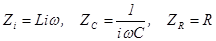 . (37)
. (37)
Для произвольного контура сложной электрической цепи имеет место комплексный аналог первого и второго законов Кирхгофа.
Если цепь содержит линейный усилитель напряжения, то есть устройство, в котором есть два входных и два выходных контакта, причем напряжения на входе и на выходе связаны в данном случае соотношением:
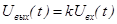 , (38)
, (38)
где 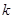 - коэффициент усилителя, то мы рассматриваем
- коэффициент усилителя, то мы рассматриваем 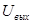 как дополнительный источник ЭДС, управляемый напряжением на входе
как дополнительный источник ЭДС, управляемый напряжением на входе 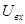 .
.
В более общем случае линейная связь между напряжением на выходе и напряжением на входе задается соотношением:
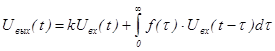 , (39)
, (39)
где 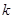 - постоянный коэффициент;
- постоянный коэффициент;
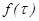 - заданная функция, характеризующая данный усилительный элемент.
- заданная функция, характеризующая данный усилительный элемент.
В соответствии с этим соотношением сигнал на выходе усилительного элемента зависит от сигнала на входе усилителя не только в данный момент времени, но и от его значений во все предыдущие моменты времени.
3. Вывод основных соотношений четырехполюсника, содержащего активные и реактивные элементы и усилитель напряжения.
Рассмотрим четырехполюсник, изображенный на рис.2:
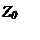 |




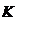
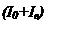
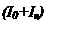
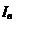
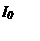
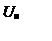
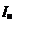
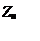
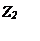
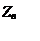
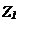
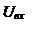
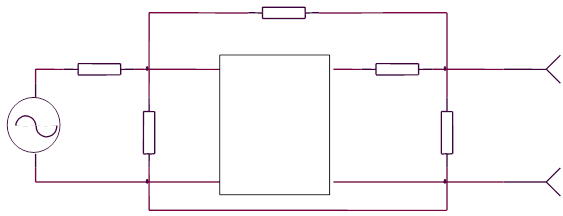
Рисунок 2. Изображение четырехполюсника. Z0 ,Z1, Z2, ZВ ,ZН -сопротивление (Ом), UВХ, UН -напряжение (В), IВ, IН, I0 -сила тока (А).
На вход четырехполюсника подается напряжение:
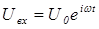 . (40)
. (40)
Усилительный элемент имеет коэффициент усиления по напряжению 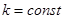 . Его входное сопротивление
. Его входное сопротивление 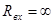 (реально может быть учтено в
(реально может быть учтено в 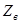 ), выходное сопротивление
), выходное сопротивление 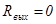 (его наличие может быть учтено в
(его наличие может быть учтено в 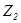 ). Величины
). Величины 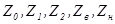 , зависящие от
, зависящие от 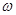 , считаются заданными. Неизвестными являются токи
, считаются заданными. Неизвестными являются токи 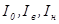 и напряжение
и напряжение 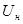 , связанное с
, связанное с 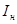 соотношением:
соотношением:
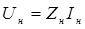 (41)
(41)
Обозначения для токов введены таким образом, что первый закон Кирхгофа для всех узлов цепи выполняется автоматически.
В соответствии со вторым законом Кирхгофа составляем систему из трех уравнений для неизвестных 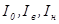 :
:
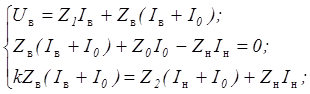
 Перепишем эту систему в стандартном виде:
Перепишем эту систему в стандартном виде:
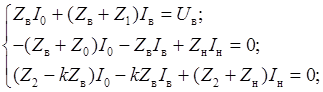 (42)
(42)
Определитель системы (3.3) 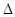 равен:
равен:
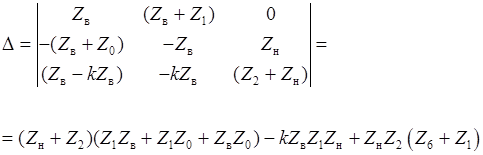 (43)
(43)
По формулам Крамера находим:
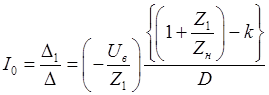 , (44)
, (44)
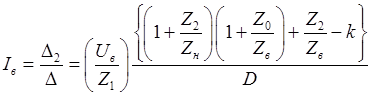 , (45)
, (45)
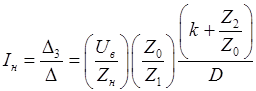 , (46)
, (46)
где для кратности введено обозначение:
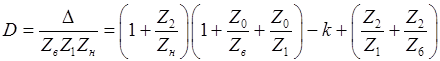 . (47)
. (47)
Коэффициент усиления четырехполюсника по напряжению 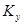 :
:
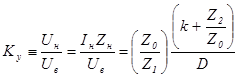 . (48)
. (48)
Входное сопротивление 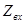 :
:
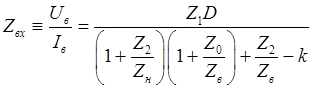 . (49)
. (49)
Напряжение холостого хода 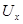 :
:
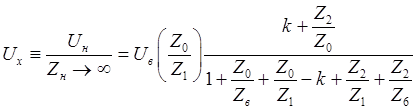 . (50)
. (50)
Выходное сопротивление усилителя 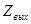 :
:
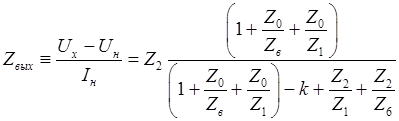 . (51)
. (51)
Если 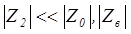 ,
, 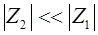 (что выполняется практически всегда), а
(что выполняется практически всегда), а 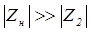 (что соответствует режиму холостого хода), то выражения (48) и (49) приобретают вид:
(что соответствует режиму холостого хода), то выражения (48) и (49) приобретают вид:
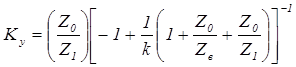 , (52)
, (52)
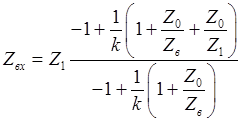 . (53)
. (53)
Соотношения (51)-(53) дают описание свойств четырехполюсника.
Остается открытым вопрос об устойчивости схемы. Характеристические уравнения для системы, аналогичные (29), получаются, если в выражении для определителя 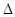 (44) сделать замену
(44) сделать замену 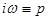 и найти корни уравнения:
и найти корни уравнения:
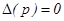 . (54)
. (54)
Для примера рассмотрим ситуацию, когда все сопротивления четырехполюсника, за исключением 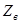 , являются действительными:
, являются действительными:
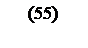
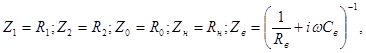
(параллельно активному сопротивлению 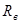 включена емкость
включена емкость 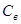 ).
).
Имеем:
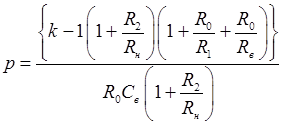 . (56)
. (56)
Из условия устойчивости, которое в общем виде имеет вид:
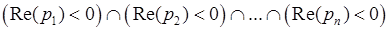 , (57)
, (57)
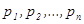 - корни характеристического уравнения, которое в нашем случае имеет вид:
- корни характеристического уравнения, которое в нашем случае имеет вид: 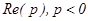 .
.
Имеем:
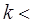
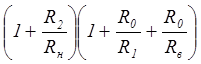 . (58)
. (58)
Из этого уравнения видно, что такая схема устойчива всегда при любых соотношениях 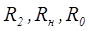 , если
, если 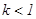 . В частности, если
. В частности, если 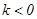 .
.
Предполагая, что 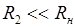 , условие устойчивости (58) можно записать в виде:
, условие устойчивости (58) можно записать в виде:
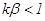 , где
, где
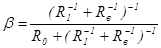 есть коэффициент ослабления делителя напряжения, составленного из сопротивления обратной связи
есть коэффициент ослабления делителя напряжения, составленного из сопротивления обратной связи 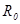 и включенных параллельно входу усилительного элемента сопротивлений
и включенных параллельно входу усилительного элемента сопротивлений 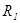 и
и 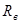 .
.
Амплитудно-частотная и фазово-частотная характеристики.
Амплитудно-частотная характеристика (АЧХ) - это графическое изображение зависимости коэффициента K усиления от частоты f. По вертикальной оси откладывается коэффициент усиления в линейном или логарифмическом масштабе, или выходное напряжение, соответствующее неизменному входному, по горизонтальной оси откладывается частота (или угловая частота ω = 2πf),в линейном или логарифмическом масштабе. Логарифмический масштаб на оси частот применяют вследствие широкого диапазона рабочих частот. Диапазоном рабочих частот называют полосу частот от нижней fн до верхней fв, в пределах которой абсолютная величина (модуль) коэффициента усиления, иногда и его фаза не должны выходить за пределы заданных допусков. Коэффициент усиления - это отношение сигнала на выходе (т. е. напряжение, ток, мощность и пр.) к сигналу на входе. АЧХ является графическим изображением того самого отношения. По виду АЧХ можно определить очень многое: диапазон рабочих частот, коэффициент усиления, нижнюю граничную частоту, верхнюю граничную частоту и многое другое.
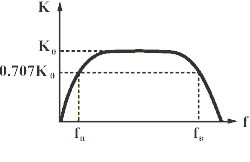
Рисунок 3. График АЧХ, где f- частота (Гц) , K- коэффициент усиления
Вот такой вид имеет график реального усилителя. Загиб вниз кривой называется спадом частот, загиб вверх - подъемом. В действительности речь идет о подъеме и спаде уровня сигналов на соответствующих частотах. 0,707 К0 - это относительный коэффициент усиления по уровню 0,707 или единица на корень из двух.
Относительный коэффициент усиления определяется, как отношение коэффициентов усиления на всех частотах к коэффициенту усиления на средней частоте. Для звукотехники принято значение средней частоты, равное
1 кГц.На частоте 1 кГц должно быть максимальное усиление, поэтому на других частотах должен быть небольшой спад, хотя в идеале значения коэффициентов усиления на всех частотах должны быть одинаковыми. Таким образом, относительный коэффициент усиления будет равен одному. Например: усилитель с коэффициентом усиления на частоте 100 Гц, равным 4,8, 500 Гц - 4,9, 1 кГц - 5, 2 кГц - 4,9, 5 кГц - 4,8. На частоте 1 кГц относительный коэффициент усиления составит 1 (5/5=1), 500 Гц - 0,98, 100 Гц - 0,96 и т. п. Образуется тот самый график с подъемом и спадом. За один принимается максимальный коэффициент усиления, а на уровне 0,707 определяются граничные частоты или полоса пропускания - промежуток между нижней и верхней рабочими частотами на уровне 0,707 относительного коэффициента усиления.
 |
Рисунок 4- График ФЧХ, где: φ- угол сдвига фазы(рад), f- частота (Гц).
Фазо-частотная характеристика (ФЧХ) - это зависимость угла сдвига фазы φ между выходным и входным напряжениями от частоты. Ухо человека не реагирует на изменения фазы гармонических сигналов, поэтому ФЧХ редко используется для описания электроакустических устройств. Искажения фазы могут привести к искажению формы звуковых колебаний, более сложных, нежели гармонический сигнал. На рисунке показана ФЧХ усилителя.
5. Расчетная часть параметров четырехполюсника
Дано:
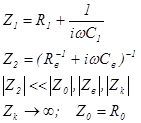
Требуется определить:
1. амплитудно-частотную и фазо-частотную характеристики усилителя;
2. абсолютную величину входного и выходного сопротивлений четырехполюсника для одной из частот 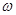 в области максимума коэффициента усиления;
в области максимума коэффициента усиления;
3. определить коэффициент чувствительности ( 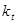 ) коэффициента усиления четырехполюсника к изменению параметра
) коэффициента усиления четырехполюсника к изменению параметра 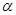 (в качестве
(в качестве 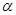 может выступать
может выступать 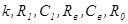 ). Для одной из частот в области max и коэффициенту усиления соответствует соотношение:
). Для одной из частот в области max и коэффициенту усиления соответствует соотношение: 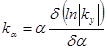 . Расчеты проводить в области частот, охватывающих низкочастотный и высокочастотный спад коэффициента усиления с дискретностью:
. Расчеты проводить в области частот, охватывающих низкочастотный и высокочастотный спад коэффициента усиления с дискретностью: 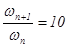 с точностью
с точностью 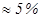 ;
;
4. построить амплитудно-частотную характеристику коэффициента усиления в двойном логарифмическом масштабе;
5. построить фазо-частотную характеристику в полулогарифмическом масштабе.
Расчетные формулы
Основные соотношения для вычисления:
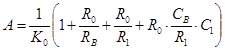 , (1)
, (1)
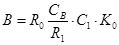 , (2)
, (2)
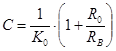 , (3)
, (3)
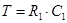 , (4)
, (4)
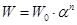 , (5)
, (5)
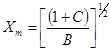 , (6)
, (6)
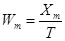 , (7)
, (7)
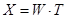 , (8)
, (8)
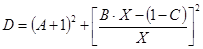 , (9)
, (9)
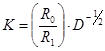 , (10)
, (10)
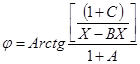 , (11)
, (11)
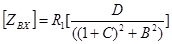 , (12)
, (12)
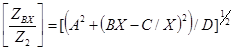 , (13)
, (13)
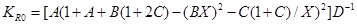 , (14)
, (14)
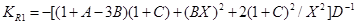 , (15)
, (15)
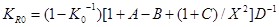 , (16)
, (16)
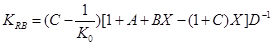 , (17)
, (17)
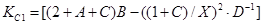 , (18)
, (18)
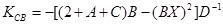 , (19)
, (19)
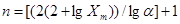 , (20)
, (20)
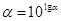 , (21)
, (21)
zвых /z2=((A2+(BX)-(C/X))((BX)-(C/X))/D. (22)
A,B,C – вспомогательные параметры, которые определяются по формулам 1-4 и далее через них высчитываем X,D,K . Вычисления зависимых параметров производят с логарифмическим шагом определяемым по формуле (5).
Полученные данные вносятся в таблицу. Данные таблицы используются для построения графиков.
Таблица расчетов
Таблица 1
Начальные данные
| Ko | R1 (Ом) | Ro (Ом) | Rв (Ом) | C1 (ф) | Cв (ф) | a |
| 0,000001 | 0,000000000001 | 0,000001 |
Таблица 2
Вспомогательные параметры
| А | 2,001001 |
| В | 0,000001 |
| С | 1,001 |
| T | 0,01 |
| Xm | 1414,567072 |
| Wm | 141456,7072 |
| Хнач | 0,01 |
| Хкон |
Таблица 3
Полоса пропускания четырёхполюсника на уровне 0,7 от Кmax
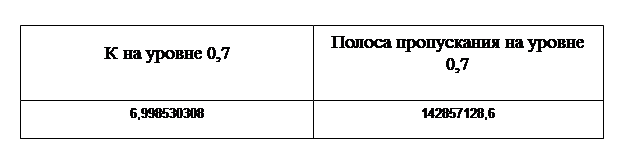
Таблица 4
Полученные значения коэффициента усиления входного сопротивления, вспомогательных параметров ,угла сдвига фаз.
| X | W | D | K | Y | |Zвх| | |Zвх/Z2| |
| 0,01 | 40049,016 | 4,996939312 | 29,89458073 | 100022492,5 | 0,50029355 | |
| 0,1 | 409,406103 | 49,42228762 | 29,03665239 | 1022492,509 | 0,50450474 | |
| 13,010004 | 277,2434439 | 21,14174302 | 32492,50937 | 0,62030728 | ||
| 9,04604301 | 332,4839427 | 3,770372178 | 22592,50937 | 0,66613247 | ||
| 9,00640341 | 333,2148149 | 0,380075938 | 22493,50939 | 0,66677135 | ||
| 9,006008004 | 333,2221297 | 0,019111309 | 22492,52187 | 0,66677781 | ||
| 9,00610304 | 333,2203715 | -0,187095884 | 22492,75922 | 0,66678246 | ||
| 9,016003 | 333,0373761 | -1,902517859 | 22517,48439 | 0,66723961 | ||
| 10,006003 | 316,132893 | -14,99497757 | 24990,01124 | 0,70717755 | ||
| 109,006003 | 95,77999109 | -28,08709719 | 272242,6967 | 0,97678689 | ||
| 10009,006 | 9,995500038 | -29,79907748 | 24997511,25 | 0,99975009 | ||
| 1E+11 | 1000009,006 | 0,999995497 | -29,97090112 | 0,9999975 |
Таблица 5
Полученные значения вспомогательных параметров углов сдвига фаз, отношение выходного сопротивления к сопротивлению второго резистора.