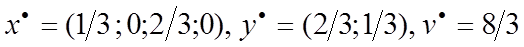Геометрический метод решения игр

Геометрический метод решения применим только к играм, в которых хотя бы один игрок имеет только две стратегии. Чаще всего к такому виду игра приводится после упрощения исходной платежной матрицы.

Если в игре (2×n)или(m×2)с нулевой суммой нет оптимального решения в чистых стратегиях, то оптимальное решение в смешанных стратегиях содержит не более двух чистых.

Графическое решение игры вида (2×n).

Рассмотрим решение задачи (2×n)на примере задачи (2х4)

Игра задана платежной матрицей:

стратегии	В1	В2	В3	В4	αi
А1 А2				-1	-1
bj

Видим, что игра не имеет седловой точки, так как α = 2 < 3.

Пусть вероятность применения игроком А стратегии А₁ равна р₁, стратегии А₂ равна р₂. Введем следующие обозначения смешанных стратегий игрока А:

р₁= х₁ и р₂= х₂ = 1 - х₁.

Найдем оптимальное решение игрока А. Найдем ожидаемые выигрыши игрока А, соответствующие чистым стратегиям игрока В.

b₁ = 2х₁ + 4х₂

b₂ = 2х₁ + 3х₂

b₃ = 3х₁ + 2х₂

b₄ = -1х₁ + 6х₂

Подставляя в эти выражения х₂ = 1 - х₁, сформируем таблицу выигрышей игрока А.

Чистые стратегии игрока В	Ожидаемые выигрыши игрока А
B1 B2 B3 B4	-2x1 + 4 -x1 + 3 x1 + 2 -2x1 + 6

Изобразим на осях х₁, х₂ четыре прямые, соответствующие линиям выигрыша, которые являются графиками этих функций от x₁.

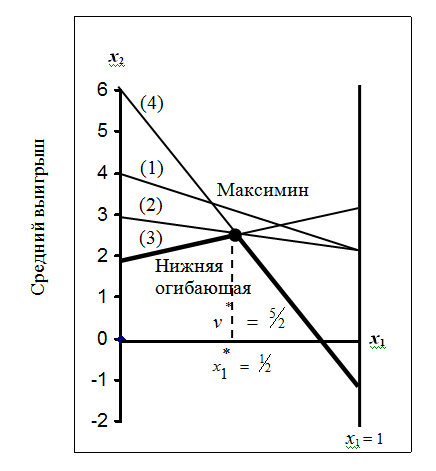
Максиминная точка определяется как самая верхняя точка на нижней огибающей этих прямых (жирная линия). В этой точке пересекаются любые две из прямых 2, 3, 4. Оптимальное решение определим из пересечения любых двух из этих прямых, имеющих противоположные наклоны, например, прямые 2, 3:

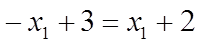, откуда 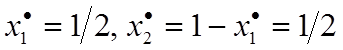, тогда цена игры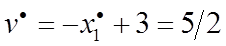

Получим оптимальное решение игрока А:

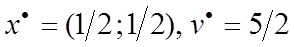
Теперь найдем оптимальное решение в смешанных стратегиях для игрока В. Вероятности применения игроком В своих стратегий q_j обозначим через y_j. Поскольку оптимальная стратегия игрока А определялась из равенства выражений 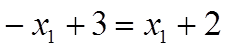, соответствующих 2-ой 3-ей чистым стратегиям игрока В, то вероятности стратегий В₁ и В₄ равны нулю, сумма вероятностей всех стратегий игрока В равна 1. Следовательно, получим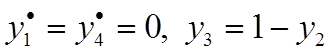

Ожидаемые проигрыши игрока В, соответствующие чистым стратегиям А, получим из соотношений

α₁ = 2у₂ + 3у₃

α₂ = 3у₂ + 2у₃

Подставляя значение у₃ = 1 – у₂, получим таблицу проигрышей игрока В

Чистые стратегии игрока А	Ожидаемые проигрыши игрока В
А1 А2	-y2 + 3 y2 + 2

Оптимальное решение, соответствующее минимаксной точке определяется из равенства: 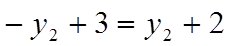, откуда ,

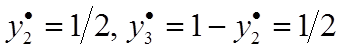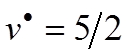
Оптимальное решение игрока В: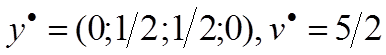

Таким образом, оптимальное решение игры:

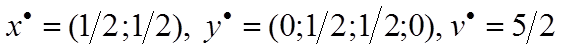
Графическое решение игры вида (m×2).

Рассмотрим решение задачи(m×2) на примере задачи (4х2)

Игра задана платежной матрицей:

стратегии	В1	В2	αi
А1 А2 А3 А4	-2		-2
bj

Решение.

Пусть y₁ и y₂ = 1 - y₁ – смешанные стратегии игрока B. Найдем оптимальное решение игрока B.

Ожидаемые проигрыши игрока В, соответствующие чистым стратегиям игрока А, приведены в таблице.

Чистые стратегии игрока А	Ожидаемые проигрыши игрока В
А1 А2 А3 А4	-2y1 + 4 -y1 + 3 y1 + 2 -8y1 + 6

На рисунке изображены четыре прямые, являющиеся графиками этих функций от y₁.

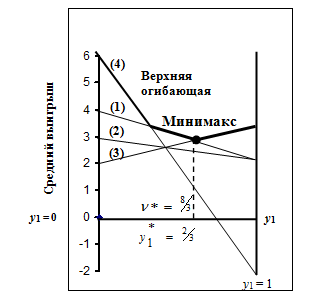
Минимальная точка определяется как самая низкая точка на верхней огибающей.

В этой точке пересекаются две прямые 1, 3. Оптимальное решение определим из пересечения этих прямых:

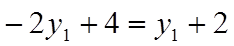, откуда ,

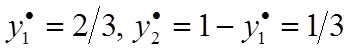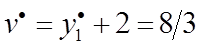
Оптимальное решение игрока B: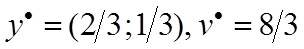

Найдем оптимальное решение игрока Ав смешанных стратегиях. Прямые, пересекающиеся в минимаксной точке, соответствуют чистым стратегиям 1 и 3 игрока А. Это означает, что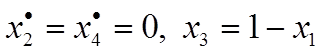

Ожидаемые проигрыши игрока А, соответствующие чистым стратегиям В, представлены в таблице.

Чистые стратегии игрока В	Ожидаемые проигрыши игрока А
В1 В2	-x1 + 3 2x1 + 2

Из уравнения 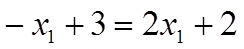находим 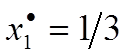, тогда .

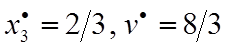Оптимальное решение игрока А: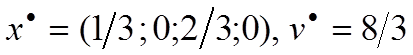

Таким образом, оптимальное решение игры: